В [1] вводится пять аксиом и доказывается существование функции полезности. Дадим содержательное представление этих аксиом. Обозначим через х, у, z различные исходы (результаты) процесса выбора, а через р, q вероятности тех или иных исходов.
Введем определение лотереи. Лотереей называется игра с двумя исходами: исходом х, получаемым с вероятностью р, и исходом у, получаемым с вероятностью 1-р (рис.4.1).
Примером лотереи является подбрасывание монеты. При этом, как известно, с вероятностью р=0,5 выпадает орел или решка. Пусть х=$10 и у=—$10 (т. е. мы получаем $10 при выпадении орла и платим столько же при выпадении решки).
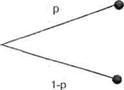
Рис.4.1. Представление лотереи
Ожидаемая (или средняя) цена лотереи определяется по формуле рх+(1-р)у.
Приведем аксиомы рационального выбора.
Аксиома 1. Исходы х, у, z принадлежат множеству А исходов.
Аксиома 2. Пусть Р означает строгое предпочтение (похожее на отношение > в математике); R — нестрогое предпочтение (похожее на отношение ≥); I - безразличие (похожее на отношение =). Ясно, что R включает Р и I. Аксиома 2 требует выполнения двух условий:
1)связанности: либо xRy, либо yRx, либо то и другое вместе;
2)транзитивности: из xRy и yRz следует xRz.
Аксиома 3. Две представленные на рис. 4.2 лотереи находятся в отношении безразличия.
Справедливость этой аксиомы очевидна. Она записывается в стандартном виде как ((х, р, y)q, у) I (x, pq, у).
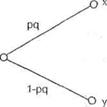
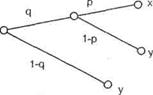
Рис.4.2. Две лотереи, находящиеся в отношении безразличия
Аксиома 4. Если xIy, то (х, р, z) I (у, р, z)
Аксиома 5. Если хРу, то хР(х, р, у)Ру.
Аксиома 6. Если xPyPz, то существует вероятность р, такая что yI(x, р, z).
Все приведенные выше аксиомы достаточно просты для понимания и кажутся очевидными.
В предположении, что они выполняются, была доказана следующая теорема [1]: если аксиомы 1—6 удовлетворяются, то существует численная функция U, определенная на А (множество исходов) и такая, что:
1) xRy тогда и только тогда, когда U(x)> U(y);
2) U(x, р, у) = pU(x)+(l-p)U(y).
Функция U(x) измеряется на шкале интервалов. Функция U(x) - единственная с точностью до линейного преобразования (например, если U(x)> U(y), то и aU(x) > aU(y), где а - целое положительное число).
Парадоксы выбора
Рассмотрим известный парадокс Алле [3] (предложенный французским ученым М.Алле), представленный двумя лотереями на рис.4.3.
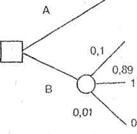
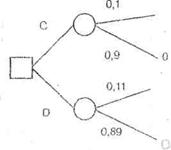
Рис.. Парадокс Алле
Обозначим: U(5 млн)=1; U (1 млн)=U; U(0)=0. В левой лотерее есть выбор между действиями А (получить 1 млн) и В (согласиться на лотерею). Подавляющее большинство людей предпочитает А. Из этого следует U>0,1 × 1+0,89× U или U>10/l=11.
В правой лотерее есть выбор между действиями С и D (две лотереи). Подавляющее большинство людей предпочитает действие С (почти та же вероятность проиграть, но выигрыш больше).Тогда 1×0,1>0,11×U, т.е U<10/11. Совершая такой выбор, люди действуют не в соответствии с функцией полезности.
Приведем еще один пример. Рассмотрим две лотереи, показанные на рис. 4.4. Легко убедиться в том, что средняя цена лотерей одинакова. Но это не означает, что людям безразлично, какую из них выбрать. Подчеркнем, что свобода выбора остается за ЛПР. Предъявление различным группам людей пар лотерей показало, что люди предпочитают правую лотерею, где при той же средней цене риск проигрыша исключен.
Как же можно объяснить такое поведение людей? Может быть, стоит усомниться в существовании функции полезности? Этот воцрос становится еще более существенным для задач принятия решений, в которых нет информации для объективного подсчета вероятностей. В таких задачах (а их гораздо больше, чем формальных задач с вазами) только эксперты могут дать значения вероятностей. Ясно, что эти значения субъективны. Потребовалось формальное обоснование теории полезности с субъективными вероятностями - теории субъективной ожидаемой полезности [5]. Она также построена аксиоматически.
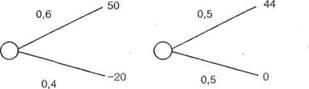
Рис. 4.4. Сравнение двух лотерей
Но и после построения этой теории остаются те же вопросы о причинах парадоксального поведения людей в задачах принятия решений, где в качестве метода выбора использовались деревья решений и максимизация субъективной ожидаемой полезности.












