Если свободные члены системы (2.1) все равны нулю, то получится однородная система уравнений:
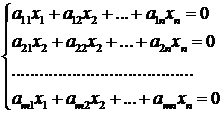 (2.3)
(2.3)
Ранг 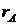 основной матрицы системы (2.3) и ранг ее расширенной матрицы
основной матрицы системы (2.3) и ранг ее расширенной матрицы 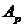 всегда равны, следовательно, однородная система всегда совместна. Нулевое решение
всегда равны, следовательно, однородная система всегда совместна. Нулевое решение 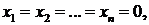 называемое тривиальным, является единственным, если
называемое тривиальным, является единственным, если 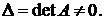 В случае, когда
В случае, когда 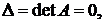 система (2.3) имеет бесчисленное множество решений.
система (2.3) имеет бесчисленное множество решений.
Пример 1. Решить систему уравнений 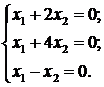
Решение. Преобразуем матрицу системы:
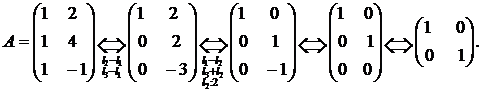
Полученная матрица, равносильная матрице данной системы, такова, что ее ранг равен двум и число неизвестных n = 2 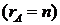 , значит система имеет единственное решение
, значит система имеет единственное решение 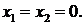
Пример 1. Решить систему уравнений 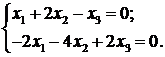
Решение. Составим матрицу 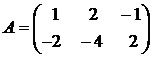 системы и найдем ее ранг:
системы и найдем ее ранг:
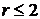 и
и 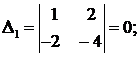
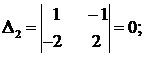
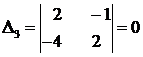 .
.
Значит, 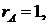 т. к., например,
т. к., например, 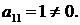
Итак, базисный минор 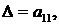 тогда базисная переменная
тогда базисная переменная 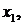 а
а 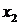
и 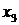 – свободные. Следовательно, решение системы
– свободные. Следовательно, решение системы 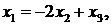 где
где 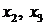 – произвольные числа.
– произвольные числа.
Если задать свободным переменным произвольные значения: 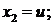
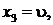 где
где 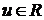 и
и 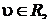 то бесчисленное множество решений системы примет вид:
то бесчисленное множество решений системы примет вид: 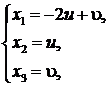 где
где 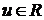 и
и 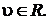
Собственные числа и собственные векторы матрицы
1. Всякий ненулевой вектор х называется собственным вектором матрицы А, если А х = l х, где l – некоторое число, называемое собственным значением (числом) матрицы 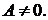
2. Если в некотором базисе вектор х и матрица А заданы:
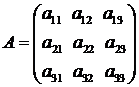 и
и 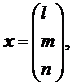 то равенству А х = l х будет эквивалентна следующая система:
то равенству А х = l х будет эквивалентна следующая система:
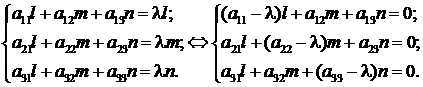 (3.1)
(3.1)
Последняя однородная система относительно неизвестных l, m, n имеет всегда нулевое решение l = 0, m = 0, n = 0, т. е. х = 0, что нас не интересует. Ненулевое решение возможно тогда и только тогда, когда определитель этой системы равен нулю, т. е.
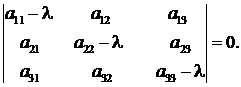 (*)
(*)
Последнее равенство называется характеристическим уравнением.
Каждый действительный корень l этого уравнения является собственным числом матрицы А. Координаты собственного вектора, соответ-ствующего каждому собственному числу, находят из системы уравне-
ний (3.1).
Замечание. Если х – собственный вектор матрицы А, то всякий, не равный нулю, коллинеарный ему вектор будет также собственным вектором матрицы А с тем же собственным числом.
Пример. Найти собственные значения и собственные векторы матрицы 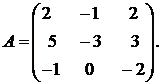
Решение. Составим характеристическое уравнение (*):
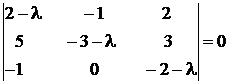 и вычислим его корни:
и вычислим его корни:
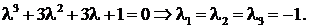 Найденное собственное число l = –1 подставим в систему уравнений (3.1) и получим:
Найденное собственное число l = –1 подставим в систему уравнений (3.1) и получим: 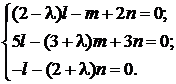
Решением последней системы являются числа: 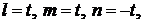
где 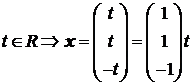 – собственный вектор данной матрицы.
– собственный вектор данной матрицы.
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие функции
Если каждому элементу х из множества D по некоторому правилу (закону) ставится в соответствие элемент у другого множества Е, то говорят, что между элементами (переменными) х и у существует функциональная зависимость; при этом переменную величину х называют независимой переменной, или аргументом, а переменную величину у – зависимой переменной, или функцией.
Функциональную зависимость между независимой переменной х и зависимой у записывают так:
 или более подробно
или более подробно 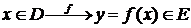 .
.
При этом множество D называется областью определения (или областью существования) функции, а множество Е – областью значения функции. Если функция f может быть задана на множестве N натуральных чисел:
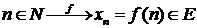 , то такая функция называется функцией натурального аргумента, или числовой последовательностью
, то такая функция называется функцией натурального аргумента, или числовой последовательностью 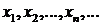 с общим членом
с общим членом 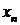 .
.
Если функция зависит от двух, трех и более аргументов, то она записывается следующим образом: 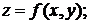
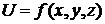 или
или 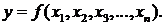
Буква f является символом правила, по которому значениям аргумента ставятся в соответствие значения функции. Если при каком-либо исследовании рассматриваются различные функции, то при их символической записи могут использоваться различные буквы: 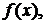
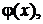
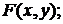
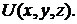
Функция считается заданной, если указано правило для определения значения функции, соответствующего данному значению аргумента. Такое правило может быть представлено различными способами. Наиболее часто встречающимися из них являются: аналитический, графический и таб-личный.
Некоторые классы функций
● Четные и нечетные функции
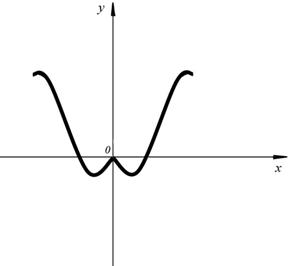 Рис. 25, а
Рис. 25, а
|  Рис. 25, б
Рис. 25, б
|
Функция  называется четной, если называется четной, если 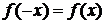 для всех х из области определения. График чет-ной функции симметричен относительно оси ординат (рис. 25, а) для всех х из области определения. График чет-ной функции симметричен относительно оси ординат (рис. 25, а)
| Функция  называется нечет-ной, если называется нечет-ной, если 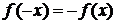 для всех х из области определения. График нечетной функции симметричен относительно начала координат (рис. 25, б) для всех х из области определения. График нечетной функции симметричен относительно начала координат (рис. 25, б)
|
Прочие функции не являются ни четными, ни нечетными, т. е. 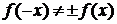 . Их графики не симметричны ни относительно оси ординат, ни относительно начала координат.
. Их графики не симметричны ни относительно оси ординат, ни относительно начала координат.
● Периодические функции
Функция  называется периодической, если существует такое постоянное число
называется периодической, если существует такое постоянное число 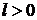 , что
, что 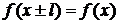 в области определения функции. При этом наименьшее из таких чисел l называется периодом:
в области определения функции. При этом наименьшее из таких чисел l называется периодом: 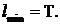
Так период функций 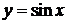 и
и  равен
равен 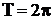 (рис. 26, а, 26, б). Период
(рис. 26, а, 26, б). Период 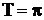 для функции
для функции 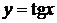 и
и 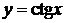 (рис. 26, в, 26, г).
(рис. 26, в, 26, г).
● Монотонные функции
Функция  называется возрастающей (убывающей) на интервале (а, b), принадлежащем области существования этой функции, если боль-шему значению аргумента х из этого интервале соответствует большее (мень-шее) значение функции. Это значит, что для возрастающей функции при значениях
называется возрастающей (убывающей) на интервале (а, b), принадлежащем области существования этой функции, если боль-шему значению аргумента х из этого интервале соответствует большее (мень-шее) значение функции. Это значит, что для возрастающей функции при значениях 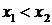 имеем неравенство
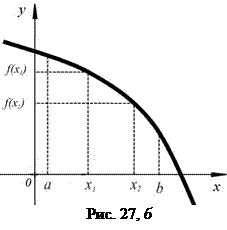
имеем неравенство 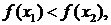 (рис. 27, а), а в случае убывания – неравенству
(рис. 27, а), а в случае убывания – неравенству 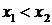 соответствует неравенство
соответствует неравенство 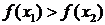 (27, б).
(27, б).
 Если функция
Если функция 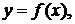 опре-деленная на интервале, является только возрастающей или только убывающей на этом интервале, то она называется монотонной на интервале.
опре-деленная на интервале, является только возрастающей или только убывающей на этом интервале, то она называется монотонной на интервале.
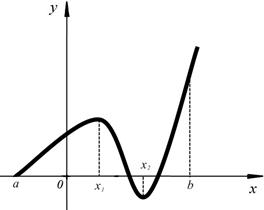
Функция

называется
кусочно-монотонной на интервале
(а, b), если на этом интервале существуют такие точки 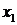 и
и 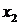 , что, например, на интервалах
, что, например, на интервалах 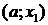 и
и 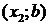 функция возрастающая, а на интервале
функция возрастающая, а на интервале 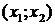 функция убывающая (рис. 27, в).
функция убывающая (рис. 27, в).
● Ограниченные функции
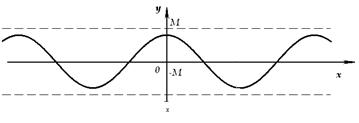 Функция
Функция  , заданная на интервале (а, b), называется ограниченной на этом интервале, если существует такое число
, заданная на интервале (а, b), называется ограниченной на этом интервале, если существует такое число 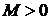 , что для всех х из данного интервала верно неравенство
, что для всех х из данного интервала верно неравенство 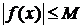 . Значит, график ограниченной функции лежит в полосе
. Значит, график ограниченной функции лежит в полосе 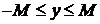 (рис. 28).
(рис. 28).
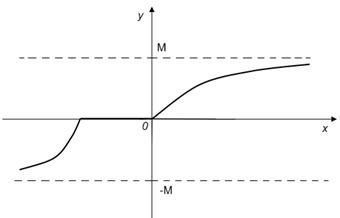
В области определения неограниченной функции существуют такие
х, что для любого числа
М будет верно неравенство:
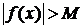
. На-пример, тригонометрические функции
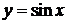
и

ограничены на всей области их существова-ния и число
М для них равно 1:
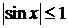
и
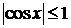
.
Неограниченными являются функции
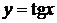
и
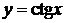
.



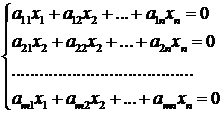 (2.3)
(2.3)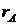 основной матрицы системы (2.3) и ранг ее расширенной матрицы
основной матрицы системы (2.3) и ранг ее расширенной матрицы 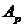 всегда равны, следовательно, однородная система всегда совместна. Нулевое решение
всегда равны, следовательно, однородная система всегда совместна. Нулевое решение 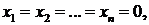 называемое тривиальным, является единственным, если
называемое тривиальным, является единственным, если 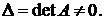 В случае, когда
В случае, когда 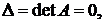 система (2.3) имеет бесчисленное множество решений.
система (2.3) имеет бесчисленное множество решений.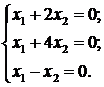
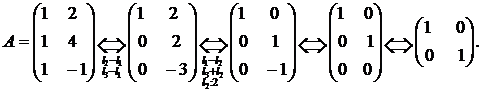
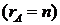 , значит система имеет единственное решение
, значит система имеет единственное решение 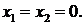
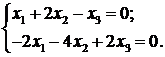
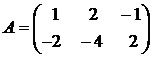 системы и найдем ее ранг:
системы и найдем ее ранг: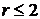 и
и 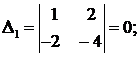
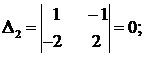
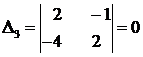 .
.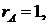 т. к., например,
т. к., например, 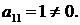
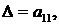 тогда базисная переменная
тогда базисная переменная 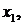 а
а 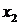
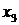 – свободные. Следовательно, решение системы
– свободные. Следовательно, решение системы 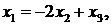 где
где 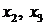 – произвольные числа.
– произвольные числа.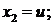
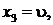 где
где 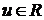 и
и 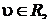 то бесчисленное множество решений системы примет вид:
то бесчисленное множество решений системы примет вид: 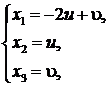 где
где 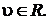
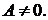
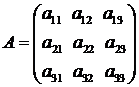 и
и 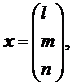 то равенству А х = l х будет эквивалентна следующая система:
то равенству А х = l х будет эквивалентна следующая система: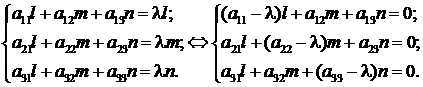 (3.1)
(3.1)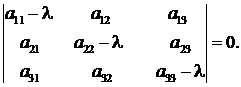 (*)
(*)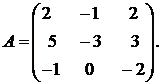
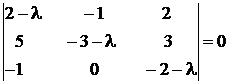 и вычислим его корни:
и вычислим его корни: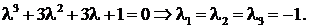 Найденное собственное число l = –1 подставим в систему уравнений (3.1) и получим:
Найденное собственное число l = –1 подставим в систему уравнений (3.1) и получим: 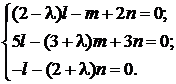
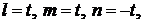
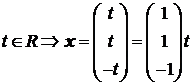 – собственный вектор данной матрицы.
– собственный вектор данной матрицы. или более подробно
или более подробно 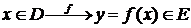 .
.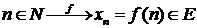 , то такая функция называется функцией натурального аргумента, или числовой последовательностью
, то такая функция называется функцией натурального аргумента, или числовой последовательностью 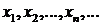 с общим членом
с общим членом 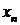 .
.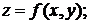
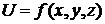 или
или 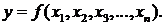
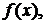
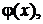
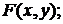
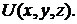
 Рис. 25, а
Рис. 25, а
 Рис. 25, б
Рис. 25, б
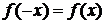 для всех х из области определения. График чет-ной функции симметричен относительно оси ординат (рис. 25, а)
для всех х из области определения. График чет-ной функции симметричен относительно оси ординат (рис. 25, а)
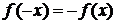 для всех х из области определения. График нечетной функции симметричен относительно начала координат (рис. 25, б)
для всех х из области определения. График нечетной функции симметричен относительно начала координат (рис. 25, б)
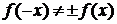 . Их графики не симметричны ни относительно оси ординат, ни относительно начала координат.
. Их графики не симметричны ни относительно оси ординат, ни относительно начала координат.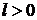 , что
, что 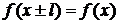 в области определения функции. При этом наименьшее из таких чисел l называется периодом:
в области определения функции. При этом наименьшее из таких чисел l называется периодом: 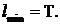
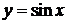 и
и  равен
равен 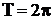 (рис. 26, а, 26, б). Период
(рис. 26, а, 26, б). Период 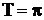 для функции
для функции 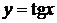 и
и 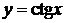 (рис. 26, в, 26, г).
(рис. 26, в, 26, г).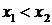 имеем неравенство
имеем неравенство 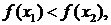 (рис. 27, а), а в случае убывания – неравенству
(рис. 27, а), а в случае убывания – неравенству 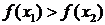 (27, б).
(27, б).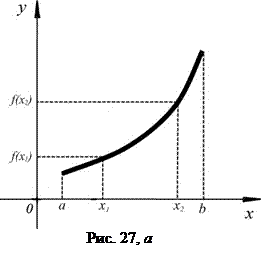
 Если функция
Если функция 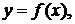 опре-деленная на интервале, является только возрастающей или только убывающей на этом интервале, то она называется монотонной на интервале.
опре-деленная на интервале, является только возрастающей или только убывающей на этом интервале, то она называется монотонной на интервале.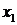 и
и 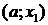 и
и 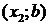 функция возрастающая, а на интервале
функция возрастающая, а на интервале 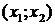 функция убывающая (рис. 27, в).
функция убывающая (рис. 27, в). Функция
Функция 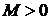 , что для всех х из данного интервала верно неравенство
, что для всех х из данного интервала верно неравенство 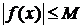 . Значит, график ограниченной функции лежит в полосе
. Значит, график ограниченной функции лежит в полосе 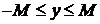 (рис. 28).
(рис. 28). В области определения неограниченной функции существуют такие х, что для любого числа М будет верно неравенство:
В области определения неограниченной функции существуют такие х, что для любого числа М будет верно неравенство: 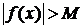 . На-пример, тригонометрические функции
. На-пример, тригонометрические функции 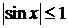 и
и 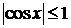 .
.


