Содержание
1. Оптимальное производственное планирование............................................................. 2
1.1. Линейная задача производственного планирования............................................. 2
1.2. Двойственная задача линейного программирования............................................. 4
1.3. Задача о расшивке узких мест................................................................................... 5
1.4. Задача о комплектном плане..................................................................................... 5
1.5. Оптимальное распределение инвестиций............................................................... 8
2. Анализ финансовых операций и инструментов........................................................... 11
2.1. Принятие решений в условиях неопределенности.............................................. 11
2.2. Анализ доходности и рискованности финансовых операций............................ 14
2.3. Задача формирования оптимальных портфелей ценных бумаг.......................... 16
2.4. Статистический анализ денежных потоков................................................ CAPut!’
3. Модели сотрудничества и конкуренции........................................................................ 23
3.1. Сотрудничество и конкуренция двух фирм на рынке одного товара................ 23
3.2. Кооперативная биматричная игра как модель сотрудничества и конкуренции 26
3.3. Матричная игра с нулевой суммой как модель сотрудничества и конкуренции 27
4. Социально-экономическая структура общества........................................................... 30
4.1. Модель распределения богатства в обществе....................................................... 30
4.2. Распределение общества по получаемому доходу................................................ 31
Список литературы................................................................................................................ 32
1. Оптимальное производственное планирование 1.1.Линейная производственная задача.
Рассмотрим предприятие, которое из m видов ресурсов производит n видов продукции. Известны нормы расхода a[i,j] – количество единиц i-го ресурса, расходуемое на производство одной единицы j-го вида продукции. Известны запасы ресурсов – i-го ресурса имеется b[i], известны удельные прибыли c[j] –прибыли от реализации одной единицы j-го вида продукции. Рассматриваемая задача состоит в нахождении допустимого плана, максимизирующего прибыль
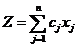 при ограничениях по ресурсам
при ограничениях по ресурсам
 .
.
Условие задачи.
45 33 30 42 удельные прибыли
нормы расхода 4 9 8 1 ¦ 220
5 2 3 0 ¦ 200
0 3 1 6 ¦ 216
запасы ресурсов
Обозначим x1,x2,x3,x4 - число единиц 1-й,2-й,3-й,4-й продукции, которые планируем произвести. При этом можно использовать только имеющиеся запасы ресурсов. Целью является получение максимальной прибыли. Получаем следующую математическую модель оптимального планирования:
P(x1, x2, x3, x4)=45x1+33x2+30x3+42x4 à max
4x1+9x2+8x3+1x4<=220
5x1+2x2+3x3+0x4<=200
0x1+3x2+1x3+6x4<=216
x1, x2, x3, x4>=0
Для решения полученной задачи в каждое неравенство добавим неотрицательную переменную. После этого неравенства превратятся в равенства, в силу этого добавляемые переменные называются балансовыми. Получается задача ЛП на максимум, все переменные неотрицательны, все ограничения есть равенства и есть базисный набор переменных: x5 - в 1-м равенстве, x6 - во 2-м и x7 - в 3-м.
P(x1,x2,x3,x4)= 45x1+33x2+30x3+42x4+0x5+0x6+0x7à max
4x1+9x2+8x3+1x4+ x5 =220
5x1+2x2+3x3+0x4 + x6 =200
0x1+3x2+1x3+6x4 + x7=216
x1,x2,x3,x4,x5,x6,x7>=0
Таблица N 1.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 220.00
|
|
|
|
|
|
|
|
|
| Х6
| 200.00
|
|
|
|
|
|
|
|
|
| Х7
| 216.00
|
|
|
|
|
|
|
|
|
| Р
| 0.00
| -45.00
| -33.00
| -30.00
| -42.00
| 0.00
| 0.00
| 0.00
|
Если все оценочные коэффициенты неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Если же есть отрицательный оценочный коэффициент, то находят самый малый из них. Если в столбце коэффициентов над ним нет положительных, то задача не имеет решения.
Оценочный коэффициент –45 самый минимальный. Ищем минимальное отношение свободных членов к положительным элементам столбца коэффициентов над самым малым отрицательным оценочным коффициентом.
Min(220/4, 200/5)=200/5.
Таблица N 2.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 60.00
| 0.00
| 7.40
| 5.60
| 1.00
| 1.00
| -0.80
| 0.00
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х7
| 216.00
| 0.00
| 3.00
| 1.00
| 6.00
| 0.00
| 0.00
| 1.00
|
|
| Р
| 1800.00
| 0.00
| -15.00
| -3.00
| -42.00
| 0.00
| 9.00
| 0.00
|
Оценочный коэффициент –42 самый минимальный.
Min(60/1, 216/6)=216/6.
Таблица N 3.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 24.00
| 0.00
| 6.90
| 5.44
| 0.00
| 1.00
| -0.80
| -0.17
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х4
| 36.00
| 0.00
| 0.50
| 0.17
| 1.00
| 0.00
| 0.00
| 0.17
|
|
| Р
| 3312.00
| 0.00
| 6.00
| 4.00
| 0.00
| 0.00
| 9.00
| 7.00
|
Все оценочные коэффициенты больше или равны 0.
Оптимальное решение: x5=24.00; x1=40.00; x4=36.00; все остальные переменные равны 0; максимум целевой функции равен 3312.00.
1.2.Двойственная задача линейного программирования.
Перейдем к рассмотрению двойственной задачи. Мы хотим найти оценку единицы каждого вида ресурса. Это – задача линейного программирования: найти вектор двойственных оценок

минимизирующий общую оценку всех ресурсов
f (y1,y2,y3) = 220*y1+200*y2+216*y3 ® min
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
4*y1+5*y2+0*y3=>45
9*y1+2*y2+3*y3=>33
8*y1+3*y2+1*y3=>30
1*y1+0*y2+6*y3=>42
причем оценки ресурсов не могут быть отрицательными

В матрично-векторном виде обе задачи (линейная и двойственная) выглядят так:
исходная задача двойственная задача
CX-->max YB-->min
AX<=B, X>=0 YA=>C, Y=>0
Запись двойственной задачи:
S= 220*y1+200*y2+216*y3 ® min
4*y1+5*y2+0*y3=>45
9*y1+2*y2+3*y3=>33
8*y1+3*y2+1*y3=>30
1*y1+0*y2+6*y3=>42
y1,y2,y3>=0
Таблица N 3.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 24.00
| 0.00
| 6.90
| 5.44
| 0.00
| 1.00
| -0.80
| -0.17
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х4
| 36.00
| 0.00
| 0.50
| 0.17
| 1.00
| 0.00
| 0.00
| 0.17
|
|
| Р
| 3312.00
| 0.00
| 6.00
| 4.00
| 0.00
| 0.00
| 9.00
| 7.00
|
Решение одной из пары двойственных задач можно найти, зная только ответ к другой задаче и пользуясь 2-й теоремой двойственности: если i-е ограничение одной из пары двойственных задач на компонентах оптимального решения есть строгое неравенство, то оптимальное значение i-й переменной другой задачи равно 0, или, что то же самое - если оптимальное значение j-й переменной одной задачи строго положительно, то j-е ограничение другой из пары двойственных задач на компонентах оптимального решения есть равенство.
Для решения необходимо и достаточно выполнение условий:
y1(4x1+9x2+8x3+1x4-220)=0, x1(4y1+5y2+0y3-45)=0,
y2(5x1+2x2+3x3+0x4-200)=0, x2(9y1+2y2+3y3-33)=0,
y3(0x1+3x2+1x3+6x4-216)=0, x3(8y1+3y2+1y3-30)=0,
x4(1y1+0y2+6y3-42)=0..
Подставим компоненты оптимального решения исходной задачи (x1=40; x2=0; x3=0; x4=36) во все уравнения этой системы. В первом уравнении выражение в скобках отлично от нуля, в силу чего y1=0. Тогда 4-е и 7-е уравнения, с учетом положительности x1 и x4, примут вид:
5y2=45
6y3=42, откуда y2=9, y3=7.
Ответ: Исходная задача: x1=40; x2=0; x3=0; x4=36; x5=24; x6=0; x7=0;
Двойственная задача: y1=0.00; y2=9.00; y3=7.00 (см. таблицу);
экстремумы целевых функций исходной и двойственной задач равны 3312.00
Таблица N 2
Цветом помечены точки с максимальным суммарным эффектом от выделения соответствующего размера инвестиций 3 предприятиям.
Таблица N 3
Цветом помечены точки с максимальным суммарным эффектом от выделения соответствующего размера инвестиций 4 предприятиям.
Сведем результаты в 4 таблицы. Теперь F4(700)=100 показывает максимальный суммарный эффект по всем 4-м фирмам, а z4(700)=200 - размер инвестиций в 4-ю фирму для достижения этого максимального эффекта. После этого на долю первых 3-х фирм осталось (700-200) и для достижения максимального суммарного эффекта по первым 3-м фирмам в 3-ю надо вложить 000 и т.д. Цветом отмечены оптимальные значения инвестиций по фирмам и значения эффектов от них.
| T
|
|
|
|
|
|
|
|
|
| F1=f1
|
|
|
|
|
|
|
|
|
| Z1=x1
|
|
|
|
|
|
|
|
|
| F2
|
|
|
|
|
|
|
|
|
| Z2
|
|
|
|
|
|
|
|
|
| F3
|
|
|
|
|
|
|
|
|
| Z3
|
|
|
|
|
|
|
|
|
| F4
|
|
|
|
|
|
|
|
|
| Z4
|
|
|
|
|
|
|
|
|
Ответ: Наилучшее распределение капитальных вложений по предприятиям: x1=100; x2=400; x3=0; x4=200
Исходные данные для анализа: ежедневные (суммарные) денежные вклады населения в отделение сбербанка в течение 4- недель (или аналогичный какой-нибудь денежный поток). Для удобства обработки все числа предполагаются целыми двузначными, что всегда можно сделать округлением и масштабированием.
Вариант данных:
| 1-я неделя
| 2-я неделя
| 3-я неделя
| 4-я неделя
|
| 1 2 3 4 5 6
| 1 2 3 4 5 6
| 1 2 3 4 5 6
| 1 2 3 4 5 6
|
|
| Денежный поток
|
|
|
| 15 14 13 9 9 9
| 9 9 9 12 12 12
| 12 12 12 2 0 16
| 18 5 4 6 5 13
|
Статистические характеристики I:
Ранжированный ряд:
0 2 4 5 5 6 9 9 9 9 9 9 12 12 12 12 12 12 13 13 14 15 16 18
Дискретный вариационный ряд:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1/24
| 1/24
| 1/24
| 2/24
| 1/24
| 6/24
| 6/24
| 2/24
| 1/24
| 1/24
| 1/24
| 1/24
|
 pi
pi
6/24
0 2 4 5 6 9 12 13 14 15 16 18 xi
Статистические характеристики II:
Интервальный вариационный ряд:
| Интервалы
| 0-2
| 2-4
| 4-6
| 6-8
| 8-10
| 10-12
| 12-14
| 14-16
| 16-18
| 18-20
|
| Центральное значение интервала
|
|
|
|
|
|
|
|
|
| CAPut!’
|
| Частоты
| 1/24
| 1/24
| 3/24
| 1/24
| 6/24
| 0/24
| 8/24
| 2/24
| 1/24
| 1/24
|
Многоугольник частостей:
График выборочной функции распределения:
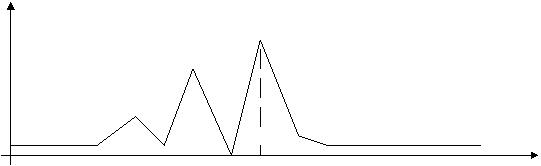


 1.По исходным данным:
1.По исходным данным:
, где еi- размер вклада, n- объем выборки


Выборочная дисперсия:
Выборочное СКО:
Несмещенная оценка генеральной дисперсии:

2. По дискретному вариационному ряду:
 ,где pi - частость, v- число вариантов выборки,
,где pi - частость, v- число вариантов выборки,
хi- одинаковые как числа элементы


Выборочная дисперсия:

Выборочное СКО:
Несмещенная оценка генеральной дисперсии:

3. По интервальному вариационному ряду:
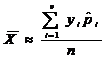
Выборочная дисперсия:
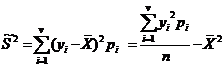
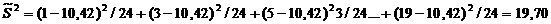
Выборочное СКО:
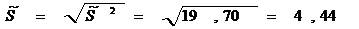
Несмещенная оценка генеральной дисперсии:
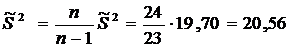
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя:

Несмещенная оценка генеральной дисперсии:
Понятие генеральной совокупности в терминах денежного потока означает все когда-либо осуществляемые вклады населения в отделение сбербанка. Понятие генеральной средней означает средний вклада среди всех когда-либо осуществлявшихся в отделение сбербанка.
5) Интервальный вариационный ряд: границы интервала [0;20], шаг h=2, число интервалов v=10.
| H=2
| [0,2)
| [2,4)
| [4,6)
| [6,8)
| [8,
10)
| [10,12)
| [12,14)
| [14,16)
| [16,18)
| [18,20)
|
|
|
|
|
|
|
|
|
|
|
|
| CAPut!’
|
| pi
| 1/24
| 1/24
| 3/24
| 1/24
| 6/24
| 0/24
| 8/24
| 2/24
| 1/24
| 1/24
|

График выборочной функции плотности:

ЛИТЕРАТУРА.
1. Математические методы принятия решений в экономике. Коллектив авторов
под редакцией Колемаева В.А., М.,Статинформ,1999.
2. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика, М., Инфра-М, 1997.
3. Колемаев В.А., Карандаев И.С., Гатауллин Т.М., Малыхин В.И. и др. Методические указания к выполнению курсовой работы по математике, ГУУ, 2000 (N 862).
4. Ершов А.Т., Карандаев И.С.,Юнисов Х.Х. Исследование операций, М., ГАУ,1991.
5. Малыхин В.И. Математика в экономике, М., Инфра-М,2000.
6. Малыхин В.И. Математическое моделирование экономики, М., УРАО,1998
7. Малыхин В.И. Финансовая математика, М., ЮНИТИ,2000.
8. Малыхин В.И. Социально-экономическая структура общества (математическое моделирование), М., ЮНИТИ, 2001.
Содержание
1. Оптимальное производственное планирование............................................................. 2
1.1. Линейная задача производственного планирования............................................. 2
1.2. Двойственная задача линейного программирования............................................. 4
1.3. Задача о расшивке узких мест................................................................................... 5
1.4. Задача о комплектном плане..................................................................................... 5
1.5. Оптимальное распределение инвестиций............................................................... 8
2. Анализ финансовых операций и инструментов........................................................... 11
2.1. Принятие решений в условиях неопределенности.............................................. 11
2.2. Анализ доходности и рискованности финансовых операций............................ 14
2.3. Задача формирования оптимальных портфелей ценных бумаг.......................... 16
2.4. Статистический анализ денежных потоков................................................ CAPut!’
3. Модели сотрудничества и конкуренции........................................................................ 23
3.1. Сотрудничество и конкуренция двух фирм на рынке одного товара................ 23
3.2. Кооперативная биматричная игра как модель сотрудничества и конкуренции 26
3.3. Матричная игра с нулевой суммой как модель сотрудничества и конкуренции 27
4. Социально-экономическая структура общества........................................................... 30
4.1. Модель распределения богатства в обществе....................................................... 30
4.2. Распределение общества по получаемому доходу................................................ 31
Список литературы................................................................................................................ 32
1. Оптимальное производственное планирование 1.1.Линейная производственная задача.
Рассмотрим предприятие, которое из m видов ресурсов производит n видов продукции. Известны нормы расхода a[i,j] – количество единиц i-го ресурса, расходуемое на производство одной единицы j-го вида продукции. Известны запасы ресурсов – i-го ресурса имеется b[i], известны удельные прибыли c[j] –прибыли от реализации одной единицы j-го вида продукции. Рассматриваемая задача состоит в нахождении допустимого плана, максимизирующего прибыль
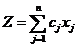 при ограничениях по ресурсам
при ограничениях по ресурсам
 .
.
Условие задачи.
45 33 30 42 удельные прибыли
нормы расхода 4 9 8 1 ¦ 220
5 2 3 0 ¦ 200
0 3 1 6 ¦ 216
запасы ресурсов
Обозначим x1,x2,x3,x4 - число единиц 1-й,2-й,3-й,4-й продукции, которые планируем произвести. При этом можно использовать только имеющиеся запасы ресурсов. Целью является получение максимальной прибыли. Получаем следующую математическую модель оптимального планирования:
P(x1, x2, x3, x4)=45x1+33x2+30x3+42x4 à max
4x1+9x2+8x3+1x4<=220
5x1+2x2+3x3+0x4<=200
0x1+3x2+1x3+6x4<=216
x1, x2, x3, x4>=0
Для решения полученной задачи в каждое неравенство добавим неотрицательную переменную. После этого неравенства превратятся в равенства, в силу этого добавляемые переменные называются балансовыми. Получается задача ЛП на максимум, все переменные неотрицательны, все ограничения есть равенства и есть базисный набор переменных: x5 - в 1-м равенстве, x6 - во 2-м и x7 - в 3-м.
P(x1,x2,x3,x4)= 45x1+33x2+30x3+42x4+0x5+0x6+0x7à max
4x1+9x2+8x3+1x4+ x5 =220
5x1+2x2+3x3+0x4 + x6 =200
0x1+3x2+1x3+6x4 + x7=216
x1,x2,x3,x4,x5,x6,x7>=0
Таблица N 1.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 220.00
|
|
|
|
|
|
|
|
|
| Х6
| 200.00
|
|
|
|
|
|
|
|
|
| Х7
| 216.00
|
|
|
|
|
|
|
|
|
| Р
| 0.00
| -45.00
| -33.00
| -30.00
| -42.00
| 0.00
| 0.00
| 0.00
|
Если все оценочные коэффициенты неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Если же есть отрицательный оценочный коэффициент, то находят самый малый из них. Если в столбце коэффициентов над ним нет положительных, то задача не имеет решения.
Оценочный коэффициент –45 самый минимальный. Ищем минимальное отношение свободных членов к положительным элементам столбца коэффициентов над самым малым отрицательным оценочным коффициентом.
Min(220/4, 200/5)=200/5.
Таблица N 2.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 60.00
| 0.00
| 7.40
| 5.60
| 1.00
| 1.00
| -0.80
| 0.00
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х7
| 216.00
| 0.00
| 3.00
| 1.00
| 6.00
| 0.00
| 0.00
| 1.00
|
|
| Р
| 1800.00
| 0.00
| -15.00
| -3.00
| -42.00
| 0.00
| 9.00
| 0.00
|
Оценочный коэффициент –42 самый минимальный.
Min(60/1, 216/6)=216/6.
Таблица N 3.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 24.00
| 0.00
| 6.90
| 5.44
| 0.00
| 1.00
| -0.80
| -0.17
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х4
| 36.00
| 0.00
| 0.50
| 0.17
| 1.00
| 0.00
| 0.00
| 0.17
|
|
| Р
| 3312.00
| 0.00
| 6.00
| 4.00
| 0.00
| 0.00
| 9.00
| 7.00
|
Все оценочные коэффициенты больше или равны 0.
Оптимальное решение: x5=24.00; x1=40.00; x4=36.00; все остальные переменные равны 0; максимум целевой функции равен 3312.00.
1.2.Двойственная задача линейного программирования.
Перейдем к рассмотрению двойственной задачи. Мы хотим найти оценку единицы каждого вида ресурса. Это – задача линейного программирования: найти вектор двойственных оценок

минимизирующий общую оценку всех ресурсов
f (y1,y2,y3) = 220*y1+200*y2+216*y3 ® min
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
4*y1+5*y2+0*y3=>45
9*y1+2*y2+3*y3=>33
8*y1+3*y2+1*y3=>30
1*y1+0*y2+6*y3=>42
причем оценки ресурсов не могут быть отрицательными

В матрично-векторном виде обе задачи (линейная и двойственная) выглядят так:
исходная задача двойственная задача
CX-->max YB-->min
AX<=B, X>=0 YA=>C, Y=>0
Запись двойственной задачи:
S= 220*y1+200*y2+216*y3 ® min
4*y1+5*y2+0*y3=>45
9*y1+2*y2+3*y3=>33
8*y1+3*y2+1*y3=>30
1*y1+0*y2+6*y3=>42
y1,y2,y3>=0
Таблица N 3.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 24.00
| 0.00
| 6.90
| 5.44
| 0.00
| 1.00
| -0.80
| -0.17
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х4
| 36.00
| 0.00
| 0.50
| 0.17
| 1.00
| 0.00
| 0.00
| 0.17
|
|
| Р
| 3312.00
| 0.00
| 6.00
| 4.00
| 0.00
| 0.00
| 9.00
| 7.00
|
Решение одной из пары двойственных задач можно найти, зная только ответ к другой задаче и пользуясь 2-й теоремой двойственности: если i-е ограничение одной из пары двойственных задач на компонентах оптимального решения есть строгое неравенство, то оптимальное значение i-й переменной другой задачи равно 0, или, что то же самое - если оптимальное значение j-й переменной одной задачи строго положительно, то j-е ограничение другой из пары двойственных задач на компонентах оптимального решения есть равенство.
Для решения необходимо и достаточно выполнение условий:
y1(4x1+9x2+8x3+1x4-220)=0, x1(4y1+5y2+0y3-45)=0,
y2(5x1+2x2+3x3+0x4-200)=0, x2(9y1+2y2+3y3-33)=0,
y3(0x1+3x2+1x3+6x4-216)=0, x3(8y1+3y2+1y3-30)=0,
x4(1y1+0y2+6y3-42)=0..
Подставим компоненты оптимального решения исходной задачи (x1=40; x2=0; x3=0; x4=36) во все уравнения этой системы. В первом уравнении выражение в скобках отлично от нуля, в силу чего y1=0. Тогда 4-е и 7-е уравнения, с учетом положительности x1 и x4, примут вид:
5y2=45
6y3=42, откуда y2=9, y3=7.
Ответ: Исходная задача: x1=40; x2=0; x3=0; x4=36; x5=24; x6=0; x7=0;
Двойственная задача: y1=0.00; y2=9.00; y3=7.00 (см. таблицу);
экстремумы целевых функций исходной и двойственной задач равны 3312.00
Расшивка «узких мест» производства.
Таблица N 3.
| C
| Б
| H
| Х1
| Х2
| Х3
| Х4
| Х5
| Х6
| Х7
|
|
| Х5
| 24.00
| 0.00
| 6.90
| 5.44
| 0.00
| 1.00
| -0.80
| -0.17
|
|
| Х1
| 40.00
| 1.00
| 0.40
| 0.60
| 0.00
| 0.00
| 0.20
| 0.00
|
|
| Х4
| 36.00
| 0.00
| 0.50
| 0.17
| 1.00
| 0.00
| 0.00
| 0.17
|
|
| Р
| 3312.00
| 0.00
| 6.00
| 4.00
| 0.00
| 0.00
| 9.00
| 7.00
|
При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, тем самым они образуют "узкие места" производства. Будем их заказывать дополнительно. Пусть T=(0,t2,t3) – вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие H+Q^(-1)>=0 или H>=-Q^(-1)T, где H -значения базисных переменных в последней симплексной таблице, а Q^(-1) - обращенный базис, который образуют столбцы при балансовых переменных в этой таблице. Задача состоит в том, чтобы найти вектор T, максимизирующий суммарный прирост прибыли W= 9t2+ 7t3 при условии, сохранения двойственных оценок ресурсов (и, следовательно ассортимента выпускаемой продукции), предполагая, что можно получить дополнительно не более 1/3 первоначального объема ресурсов каждого вида.
Графическое решение задачи о расшивке узких мест производства.
W=9t2+7t3®max. ограничивающие прямые:
|24|>=-| 1.00 0.80 -0.17| | 0| 0.80t2+0.17t3<=24
|40|>=-| 0.00 0.20 0.00| |t2| t2>=-200
|36|>=-| 0.00 0.00 0.17| |t3| t3>=-211.8
t2<=200/3; t3<=216/3
t2,t3>=0

 t3
t3
141.2

 216/3
216/3
 -200 200/3
-200 200/3
 t2
t2
0 30
-211.8

t3=72.00; 0.8t2+0.17*72=24 →t2=14.7
maxW=9t2+7t3=636.3
Ответ: t2=14.70; t3=72.00; maxW=636.3.
1.4.Задача о комплектном плане.
Задачу ЛП с двумя переменными можно решить графически. Возьмем на плоскости систему координат: ось OX1 направим горизонтально и вправо, ось OX2 - вертикально и вверх. Каждое ограничение задачи, раз оно линейное нестрогое неравенство, графически изображается полуплоскостью, граничная прямая которой соответствует уже не неравенству, а равенству. Допустимое множество задачи является пересечением всех этих полуплоскостей и есть выпуклый многоугольник.
Вторая из двух основных теорем ЛП гласит: Если экстремум целевой функции достигается на допустимом множестве, то функция принимает его в какой-то вершине многоугольника – допустимого множества. Исходя из этой теоремы, найти искомый экстремум, можно просто перебрав вершины многоугольника, и определив ту, в которой значение функции экстремально. Чаще делают по-другому: строят линию уровня целевой функции и двигают ее параллельно в направлении экстремума, стараясь уловить последнюю точку пересечения линии с допустимым множеством. Зададим задачу ЛП с тремя ограничениями и четырьмя переменными, затем зададим выражения x3 и x4 через x1 и x2. Теперь переменных осталось две и задача может быть решена графически.
Условие задачи:
45 33 30 42
-------------------------
4 9 8 1 ¦ 220
5 2 3 0 ¦ 200
0 3 1 6 ¦ 216
Принимая: x3/x1=1; x4/x2=3 – получаем:
75 159
-------------
12 12 ¦ 220 12x1+12x2<=220
8 2 ¦ 200 8x1 + 2x2<=200
1 21 ¦ 216 x1+21x2<=216
 x2
x2
100
2
 18.3 1
18.3 1

 10.3 3 x1
10.3 3 x1

0 18.3 25 216
Найдем x1 и x2: 12x1+12x2=220 x1=8.42
x1+21x2=216 x2=9.88
Оптимальное решение:
x1=8.42; x2=9.88; max=2202.42.





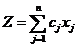 при ограничениях по ресурсам
при ограничениях по ресурсам .
.

 pi
pi




 1.По исходным данным:
1.По исходным данным:


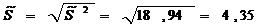

 ,где pi - частость, v- число вариантов выборки,
,где pi - частость, v- число вариантов выборки,


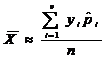
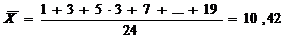
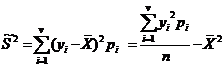
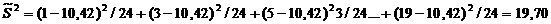
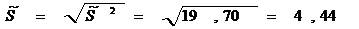
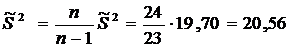

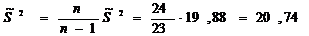





 t3
t3

 216/3
216/3
 -200 200/3
-200 200/3 t2
t2
 x2
x2

 18.3 1
18.3 1 
 10.3 3 x1
10.3 3 x1



