Содержание
Введение…………………………………………………………………………….2
1. Постановка задачи……………………………………………………………...3
2. Графическое решение задачи линейного программирования………........5
3. Решение задачи линейного программирования алгебраическим симплекс-методом………………………………………………………………7
Решение задачи линейного программирования с использованием
симплекс-таблицы……………...……………………………………………...10
Решение задачи линейного программирования методом отыскания
допустимого решения…………………………………………………………14
6. Двойственная задача линейного программирования…………………….18
Решение задачи целочисленного линейного программирования
методом «ветвей и границ»…………………………………………………..21
8. Ход решения целочисленной задачи линейного программирования
методом Гомори……………………………………………………………….25
9. Решение булевских задач ЛП методом Балаша…………………………..30
Заключение………………………………………………………………………...33
Литература………………………………………………………………………....34
Введение
Современный этап развития человечества отличается тем, что на смену века энергетики приходит век информатики. Происходит интенсивное внедрение новых технологий во все сферы человеческой деятельности. Встает реальная проблема перехода в информационное общество, для которого приоритетным должно стать развитие образования. Изменяется и структура знаний в обществе. Все большее значение для практической жизни приобретают фундаментальные знания, способствующие творческому развитию личности. Важна и конструктивность приобретаемых знаний, умение их структурировать в соответствии с поставленной целью. На базе знаний формируются новые информационные ресурсы общества. Формирование и получение новых знаний должно базироваться на строгой методологии системного подхода, в рамках которого отдельное место занимает модельный подход. Возможности модельного подхода крайне многообразны как по используемым формальным моделям, так и по способам реализации методов моделирования. Физическое моделирование позволяет получить достоверные результаты для достаточно простых систем.
В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации.
Постановка задачи
Решить задачу нахождения минимума целевой функции для системы ограничений, заданной многоугольником решений в соответствии с вариантом №16 задания. Многоугольник решений представлен на рисунке 1:
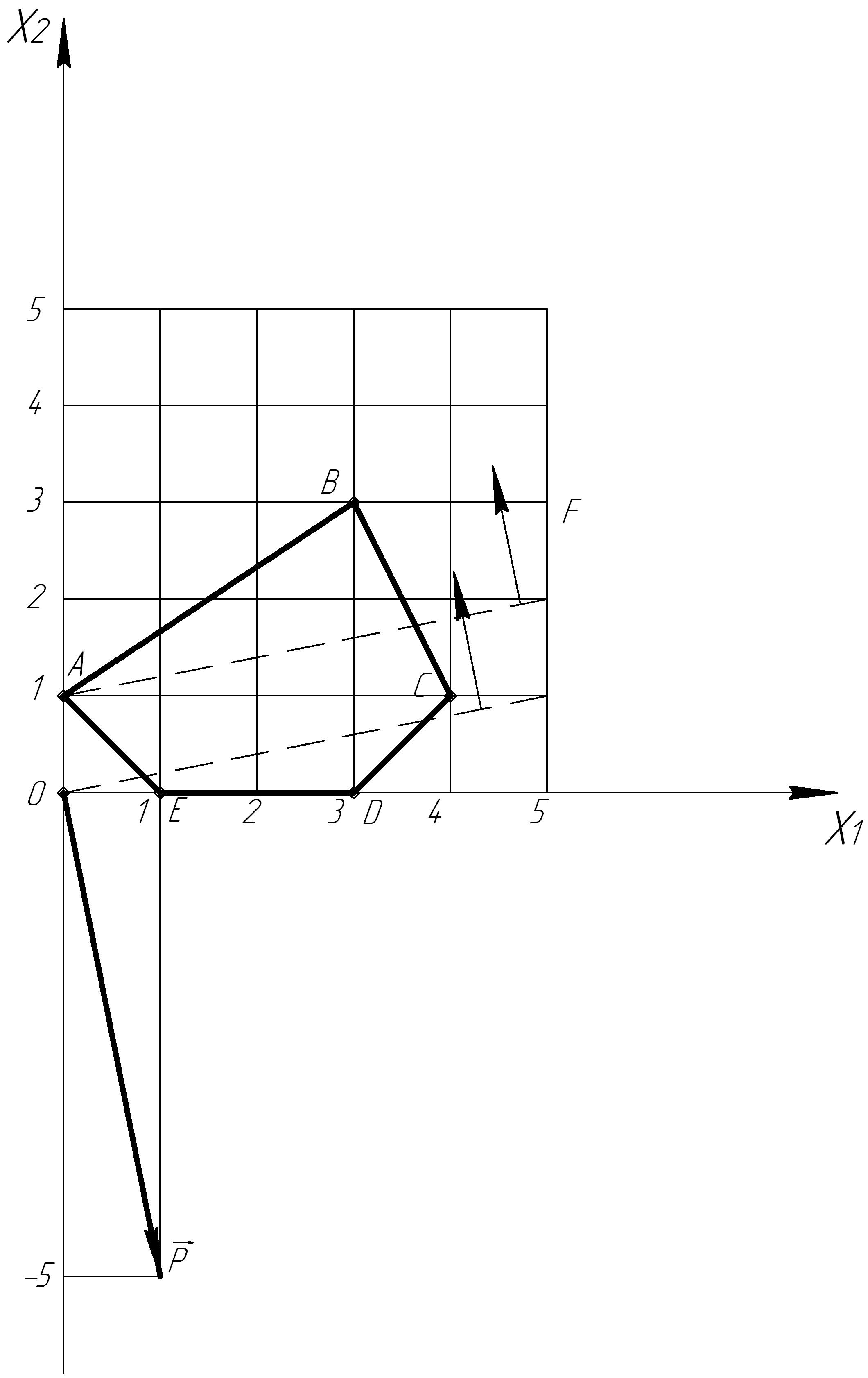
Рисунок 1 – Многоугольник решений задачи
Система ограничений и целевая функция задачи представлены ниже:


Необходимо решить задачу, используя следующие методы:
· Графический метод решения задач ЛП;
· Алгебраический метод решения задач ЛП;
· Симплекс-метод решения задач ЛП;
· Метод отыскания допустимого решения задач ЛП;
· Решение двойственной задачи ЛП;
· Метод «ветвей и границ» решения целочисленных задач ЛП;
· Метод Гомори решения целочисленных задач ЛП;
· Метод Балаша решения булевских задач ЛП.
Сравнить результаты решения разными методами сделать соответствующие выводы по работе.
Симплекс-таблицы.


Решение: Приведем задачу к стандартному виду для решения с помощью симплекс-таблицы.
Все уравнения системы приведем к виду: 


Строим симплекс-таблицу:
- В верхний угол каждой клетки таблицы вписываем коэффициенты из системы уравнений;
- Выбираем максимальный положительный элемент в строке F, кроме b, это будет генеральный столбец;
- Для того, чтобы найти генеральный элемент строим отношение  для всех положительных a. 3/3; 9/1;- минимальное соотношение в строке x3. Следовательно -
для всех положительных a. 3/3; 9/1;- минимальное соотношение в строке x3. Следовательно -  генеральная строка и a=3 - генеральный элемент.
генеральная строка и a=3 - генеральный элемент.
- Находим l=1/a=1/3. Вносим l в нижний угол клетки, где находится генеральный элемент;
- Во все незаполненные нижние углы генеральной строки вносим произведение значения в верхнем углу клетки на l;
- Выделяем верхние углы генеральной строки;
- Во все нижние углы генерального столбца заносим произведение значения в верхнем углу на -l и выделяем полученные значения;
- Остальные клетки таблицы заполняются, как произведения соответствующих выделенных элементов;
- Затем строим новую таблицу, в которой обозначения клеток элементов генерального столбца и строки меняются местами (x2 и x3);
- В верхний угол бывших генеральных строки и столбца записываются значения, которые до этого были в нижнем углу;
- В верхний угол остальных клеток записывается сумма значений верхнего и нижнего угла этих клеток в предыдущей таблице
| Свободные
Базисные
| 
| 
| 
|

|
| -2
-2/3
|
1/3
|

|
-1
|
2/3
|
-1/3
|

|
|
-2/3
| -1
1/3
|

|
|
-2/3
| -1
1/3
|

|
-5
| -1
10/3
|
-5/3
|
| Свободные
Базисные
| 
| 
| 
|

|
| -2/3
1/4
| 1/3
-1/12
|

|
| 8/3
3/8
| -1/3
-1/8
|

|
-1
| 1/3
-1/8
| 1/3
1/24
|

|
-1
| 1/3
-1/8
| 1/3
1/24
|
| -5
-7
| 7/3
-7/8
| -5/3
7/24
|
| Свободные
Базисные
| 
| 
| 
|

|
| 1/4
| 1/4
|

|
| 3/8
| -1/8
|

|
| -1/8
| 9/24
|

|
| -1/8
| 9/24
|
| -12
| -7/8
| -11/8
|
Анализируя полученные результаты, можно сделать вывод, что найдено оптимальное решение задачи линейного программирования:
| Х1 = 3, Х2 = 3, Fmin = -12
|
Методом «ветвей и границ».
Преобразуем исходную задачу таким образом, чтобы не выполнялось условие целочисленности при решении обычными методами.

Исходный многоугольник решений задачи целочисленного программирования.
Для преобразованного многоугольника решений построим новую систему ограничений.
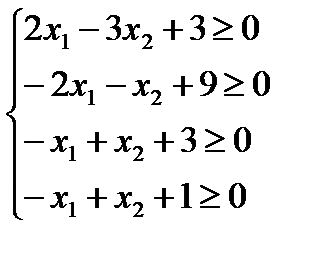

Запишем систему ограничений в виде равенств, для решения алгебраическим методом.


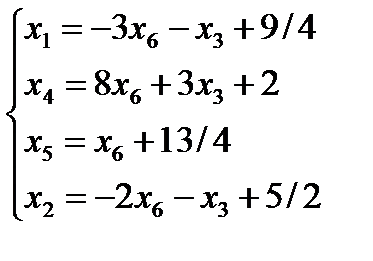

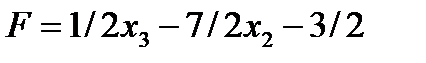

В результате решения найден оптимальный план задачи: х1 =9/4, х2 = 5/2, F =-41/4. Это решения не отвечает условию целочисленности, поставленному в задаче. Разобьем исходный многоугольник решений на две области, исключив из него область 3<x1<4. Новый многоугольник решений представлен на рисунке ниже.

Измененный многоугольник решений задачи
Составим новые системы ограничений для образовавшихся областей многоугольника решений. Левая область представляет собой четырехугольник (трапецию). Система ограничений для левой области многоугольника решений представлена ниже.


Система ограничений для левой области
Правая область представляет собой точку С.
Система ограничений для правой области решений представлена ниже.
х1 =4
х2 = 1

Система ограничений для правой области
Новые системы ограничений представляют из себя две вспомогательные задачи, которые необходимо решить независимо друг от друга. Решим задачу целочисленного программирования для левой области многоугольника решений.
 ,
, 








В результате решения найден оптимальный план задачи: х1 = 3, х2 = 3, F = -12. Этот план удовлетворяет условию целочисленности переменных в задаче и может быть принят в качестве оптимального опорного плана для исходной задачи целочисленного линейного программирования. Проводить решение для правой области решений нет смысла. На рисунке ниже представлен ход решения целочисленной задачи линейного программирования в виде дерева.
|
x1 =9/4
x2 = 5/2
F = 41/4
|
Бесперспективное
направление решения
X1 ≤ 3 X1 ³ 4
Оптимальный план
Ход решения целочисленной задачи ЛП методом «ветвей и границ»
| Х1 = 3, Х2 = 3, Fmin = -12
|
8. Ход решения целочисленной задачи линейного программирования
методом Гомори.
Во многих практических приложениях представляет большой интерес задача целочисленного программирования, в которой дана система линейных неравенств и линейная форма
 (1)
(1)
 (2)
(2)


Требуется найти целочисленное решение системы (1), которое минимизирует целевую функцию F, причем, все коэффициенты  - целые.
- целые.
Один из методов решения задачи целочисленного программирования предложен Гомори. Идея метода заключается в использовании методов непрерывного линейного программирования, в частности, симплекс-метода.
1)Определяется с помощью симплекс-метода решение задачи (1), (2), у которой снято требование целочисленности решения; если решение оказывается целочисленным, то искомое решение целочисленной задачи будет также найдено;
2) В противном случае, если некоторая координата  - не целая, полученное решение задачи проверяется на возможность существования целочисленного решения (наличие целых точек в допустимом многограннике):
- не целая, полученное решение задачи проверяется на возможность существования целочисленного решения (наличие целых точек в допустимом многограннике):
- если в какой-либо строке с дробным свободным членом  , все остальные коэффициенты
, все остальные коэффициенты  окажутся целыми, то в допустимом многограннике нет целых, точек и задача целочисленного программирования решения не имеет;
окажутся целыми, то в допустимом многограннике нет целых, точек и задача целочисленного программирования решения не имеет;
- в противном случае вводится дополнительное линейное ограничение, которое отсекает от допустимого многогранника часть, бесперспективную для поиска решения задачи целочисленного программирования;
3) Для построения дополнительного линейного ограничения, выбираем l -тую строку с дробным свободным членом  и записываем дополнительное ограничение
и записываем дополнительное ограничение
 (3)
(3)
где 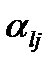 и
и  - соответственно дробные части коэффициентов
- соответственно дробные части коэффициентов  и свободного
и свободного
члена  . Введем в ограничение (3) вспомогательную переменную
. Введем в ограничение (3) вспомогательную переменную  :
:
 (4)
(4)
Определим коэффициенты 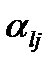 и
и  , входящие в ограничение (4):
, входящие в ограничение (4):
 (5)
(5)
где  и
и  - ближайшие целые снизу для
- ближайшие целые снизу для  и
и  соответственно.
соответственно.
4) Далее с помощью симплекс-метода снова решается задача линейного программирования при наличии дополнительного ограничения и т.д.
Гомори доказал, что конечное число подобных шагов приводит к такой задаче линейного программирования, решение которой будет целочисленным и, следовательно, искомым.


Решение: Приведем систему линейных ограничений и функцию цели к канонической форме:

Определим оптимальное решение системы линейных ограничений, временно отбросив условие целочисленности. Используем для этого симплекс-метод. Ниже последовательно в таблицах представлены исходное решение задачи, и приведены преобразования исходной таблицы с целью получения оптимального решения задачи:
| Свободные
Базисные
| 
| 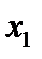
| 
|

|
| -2
-2/3
|
1/3
|

|
-1
|
2/3
|
-1/3
|

|
|
-2/3
| -1
1/3
|

|
|
-2/3
| -1
1/3
|

|
-5
| -1
10/3
|
-5/3
|
| Свободные
Базисные
| 
| 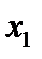
| 
|

|
| -2/3
1/4
| 1/3
-1/12
|

|
| 8/3
3/8
| -1/3
-1/8
|

|
-1
| 1/3
-1/8
| 1/3
1/24
|

|
-1
| 1/3
-1/8
| 1/3
1/24
|
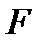
| -5
-7
| 7/3
-7/8
| -5/3
7/24
|
| Свободные
Базисные
| 
| 
| 
|

|
| 1/4
| 1/4
|

|
| 3/8
| -1/8
|

|
| -1/8
| 9/24
|

|
| -1/8
| 9/24
|
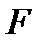
| -12
| -7/8
| -11/8
|
Из таблицы видно, что получено следующее оптимальное решение системы линейных ограничений:
Fmax = -12
XT=[3,3,0,0,3,1]
Найденная оптимальная точка является целочисленной. Целочисленность решения не нарушается по всем координатам.
Содержание
Введение…………………………………………………………………………….2
1. Постановка задачи……………………………………………………………...3
2. Графическое решение задачи линейного программирования………........5
3. Решение задачи линейного программирования алгебраическим симплекс-методом………………………………………………………………7
Решение задачи линейного программирования с использованием
симплекс-таблицы……………...……………………………………………...10










 для всех положительных a. 3/3; 9/1;- минимальное соотношение в строке x3. Следовательно -
для всех положительных a. 3/3; 9/1;- минимальное соотношение в строке x3. Следовательно -  генеральная строка и a=3 - генеральный элемент.
генеральная строка и a=3 - генеральный элемент.
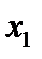








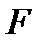

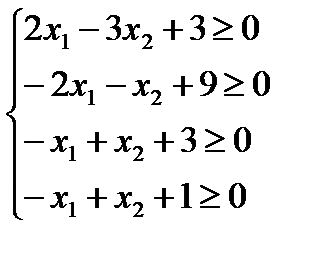



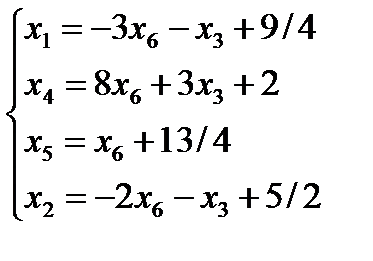

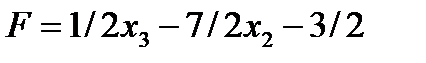









 (1)
(1) (2)
(2)

 - целые.
- целые. - не целая, полученное решение задачи проверяется на возможность существования целочисленного решения (наличие целых точек в допустимом многограннике):
- не целая, полученное решение задачи проверяется на возможность существования целочисленного решения (наличие целых точек в допустимом многограннике): , все остальные коэффициенты
, все остальные коэффициенты  окажутся целыми, то в допустимом многограннике нет целых, точек и задача целочисленного программирования решения не имеет;
окажутся целыми, то в допустимом многограннике нет целых, точек и задача целочисленного программирования решения не имеет; (3)
(3)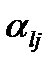 и
и  - соответственно дробные части коэффициентов
- соответственно дробные части коэффициентов  :
: (4)
(4) (5)
(5) и
и  - ближайшие целые снизу для
- ближайшие целые снизу для 


