Пусть дана система линейных алгебраических уравнений:
 (1)
(1)
Можно предположить, что все  , в противном случае умножаем соответствующее уравнение на -1.
, в противном случае умножаем соответствующее уравнение на -1.
Вводим вспомогательные переменные:
 (2)
(2)
Вводим так же вспомогательную функцию 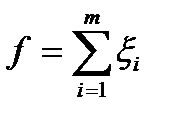 (3)
(3)
Будем минимизировать систему при ограничениях (2) и условиях  .
.
ПРАВИЛО ОТЫСКАНИЯ ДОПУСТИМОГО РЕШЕНИЯ: Для отыскания допустимого решения системы (1) минимизируем форму (3) при ограничениях (2), в качестве свободных неизвестных берем xj, в качестве базисных  .
.
При решении задачи симплекс-методом могут возникнуть два случая:
1. min f=0, тогда все xi обязаны быть равными нулю. А получившиеся значения xj будут составлять допустимое решение системы (1).
2. min f>0, т.е. исходная система не имеет допустимого решения.
Исходная система:
Используется условие задачи предыдущей темы.

 (4)
(4)
Внесем дополнительные переменные:
 (5)
(5)
Заполняем симплекс-таблицу:
| Св.
Баз.
|
|
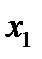
|

|
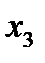
|

|

|

|

|
-2
|
-2
|
|
|
|
|
-2
|

|
| -2
|
-2
|
|
|
|
|

|
-2
|
-2
|
|
|
|
|
-2
|

|
- 1
|
-1
| -1
|
|
|
|
-1
|

|
|
| -1
-1
|
|
|
|
|

|
| -1
|
-1
|
|
|
|
|
Переменную  4 исключаем из рассмотрения.
4 исключаем из рассмотрения.
| Св.
Баз.
| 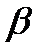
| 
| 
| 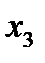
| 
| 
| 
|

|
-28/3
|
|
-4/3
|
|
-4/3
|
| -1
8/3
|

|
-7/3
|
|
-1/3
|
|
-1/3
|
|
2/3
|

|
7/3
|
|
1/3
|
|
1/3
|
| -2
-2/3
|

|
|
|
|
|
|
| -1
|
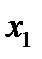
|
7/3
|
| -1
1/3
|
|
1/3
|
|
-2/3
|

|
-28/3
|
|
-4/3
|
|
-4/3
|
|
8/3
|
| Св.
Баз.
| 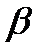
| 
| 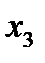
| 
|

|

|

| 14/3
-5/3
|
|
-5/8
| -1/3
5/24
|
| 5/3
-5/8
|

| 8/3
|
|
3/8
| -1/3
-1/8
|
| 8/3
3/8
|

| 7/3
2/3
|
|
1/4
| 1/3
-1/12
|
| -2/3
1/4
|

|
|
|
3/8
|
-1/8
|
| -1
3/8
|
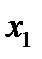
| 10/3
-1/3
|
|
-1/8
| 1/3
1/24
|
| 1/3
-1/8
|

| -25/3
-11/3
|
|
-11/8
| -4/3
11/24
|
| 11/3
-11/8
|
| Св.
Баз.
| 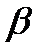
| 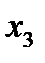
| 
| 
|

|
| 3/8
| -1/8
|
|

|
| 3/8
| -1/8
|
|

|
| 1/4
| 1/4
|
|

|
| 3/8
| -1/8
|
|
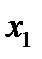
|
| -1/8
| 3/8
|
|

| -12
| -11/8
| -7/8
|
|
Найдено допустимое решение исходной задачи: х1 = 3, х2 = 3, F = -12. Основываясь на полученном допустимом решении найдем оптимальное решение исходной задачи, пользуясь симплекс-методом. Для этого построим новую симплекс-таблицу из таблицы полученной выше, удалив строку  и строку с целевой функцией вспомогательной задачи:
и строку с целевой функцией вспомогательной задачи:
| Св.
Баз.
| 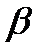
| 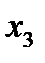
| 
| 
|

|
| 3/8
| -1/8
|
|

|
| 1/4
| 1/4
|
|
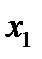
|
| -1/8
| 3/8
|
|

| -12
| -11/8
| -7/8
|
|
Анализируя построенную симплекс-таблицу, видим, что оптимальное решение для исходной задачи уже найдено (элементы в строке, соответствующей целевой функции, отрицательны). Таким образом, допустимое решение, найденное при решении вспомогательной задачи совпадает с оптимальным решением исходной задачи:
| Х1 = 3, Х2 = 3, Fmin = -12
|
6. Двойственная задача линейного программирования
Исходная система ограничений и целевая функция задачи показаны на рисунке ниже.

при ограничениях:

Решение: Приведем систему ограничений к стандартному виду:

Задача, двойственная данной будет иметь вид:
 ,
,

Решение двойственной задачи будет выполняться простым симплекс-методом.
Преобразуем целевую функцию так, чтобы решалась задача минимизации, и запишем систему ограничений в стандартной форме для решения симплекс-методом.
y6 = 1 – (-2 y1 + 2y2 +y3 + y4+ y5)
y7 = 5 – (-3y1 - y2 + y3 + y4)
Ф = 0 – (3y1 + 9y2 + 3y3 + y4 ) ® min
Построим исходную симплекс-таблицу для решения двойственной задачи ЛП.
|
| b
| Y1
| Y2
| Y3
| Y4
| Y5
|
| Y6
|
1/2
| -2
-1
|
1/2
|
1/2
|
1/2
|
1/2
|
| Y7
|
1/2
| -3
-1
| -1
1/2
|
1/2
|
1/2
|
1/2
|
| Фmin
|
-9/2
|
|
-9/2
|
-9/2
|
-9/2
|
-9/2
|
Первый шаг симплекс-метода
|
| b
| Y1
| Y6
| Y3
| Y4
| Y5
|
| Y2
| 1/2
-11/8
| -1
-1/4
| 1/2
-1/8
| 1/2
-3/8
| 1/2
-3/8
| 1/2
-1/8
|
| Y7
| 11/2
-11/8
| -4
-1/4
| 1/2
-1/8
| 3/2
-3/8
| 3/2
-3/8
| 1/2
-1/8
|
| Фmin
| -9/2
33/2
|
| -9/2
3/2
| -3/2
9/2
| -7/2
9/2
| -9/2
3/2
|
Второй шаг симплекс-метода
|
| b
| Y1
| Y6
| Y3
| Y4
| Y5
|
| Y2
| 1/2
-11/8
| -1
-1/4
| 1/2
-1/8
| 1/2
-3/8
| 1/2
-3/8
| 1/2
-1/8
|
| Y7
| 11/2
-11/8
| -4
-1/4
| 1/2
-1/8
| 3/2
-3/8
| 3/2
-3/8
| 1/2
-1/8
|
| Фmin
| -9/2
33/2
|
| -9/2
3/2
| -3/2
9/2
| -7/2
9/2
| -9/2
3/2
|
Третий шаг симплекс-метода
|
| b
| Y7
| Y6
| Y3
| Y4
| Y5
|
| Y2
| -7/8
| -1/4
| 3/8
| 1/8
| 1/8
| 1/8
|
| Y1
| -11/8
| -1/4
| -1/8
| -3/8
| -3/8
| -1/8
|
| Фmin
|
|
| -3
|
|
| -3
|
Итак, на третьем шаге симплекс-метода найдено оптимальное решение задачи минимизации со следующими результатами: y2 = -7 /8, y1 = -11/8, Ф = 12. Для того, чтобы найти значение целевой функции двойственной задачи, подставим найденные значения базисных и свободных переменных в функцию максимизации:
Фmax = - Фmin = 3*(-11/8) + 9(-7/8) + 3*0 + 0 = -12
Так как значение целевой функции прямой и двойственной задач совпадают, решение прямой задачи найдено и равно 12.
Fmin = Фmax = -12



 (1)
(1) , в противном случае умножаем соответствующее уравнение на -1.
, в противном случае умножаем соответствующее уравнение на -1. (2)
(2)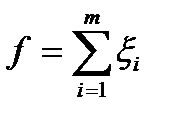 (3)
(3) .
. .
.
 (4)
(4) (5)
(5)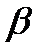
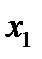

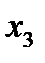









 4 исключаем из рассмотрения.
4 исключаем из рассмотрения.

 ,
,



