

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
Пусть материальная точка М движется прямолинейно по закону S = f(t). Как уже известно, производная St’ равна скорости точки в данный момент времени: St’= V.
Пусть в момент времени t скорость точки равна V, а в момент t +Dt – скорость равна V + DV, т. е. за промежуток времени Dt скорость изменилась на величину DV.
Отношение 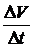 выражает среднее ускорение движения точки за время Dt. Предел этого отношения при Dt ®0 называется ускорением точки М в данный момент t и обозначается буквой а:
выражает среднее ускорение движения точки за время Dt. Предел этого отношения при Dt ®0 называется ускорением точки М в данный момент t и обозначается буквой а: 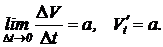 Итак, вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т. е.
Итак, вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т. е. 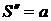 .
.
Дифференциалы высших порядков
Пусть y=f(x) дифференцируемая функция, а ее аргумент х – независимая переменная. Тогда ее первый дифференциал 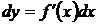 есть также функция х, можно найти дифференциал этой функции.
есть также функция х, можно найти дифференциал этой функции.
Дифференциал от дифференциала функции называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается 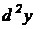 :
: 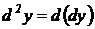 .
.
Дифференциал второго порядка от данной функции равен произведению второго порядка этой функции на квадрат дифференциала независимой переменной: 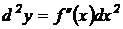 .
.
Приложение дифференциального исчисления
Функция называется возрастающей (убывающей) на интервале ( a; b), если для любых двух точек x1 и x2 из указанного интервала, удовлетворяющих неравенству 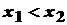 , выполняется неравенство
, выполняется неравенство 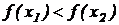 (
(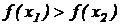 ).
).
Необходимое условие возрастания (убывания): Если дифференцируемая функция на интервале ( a, b) возрастает (убывает), то производная этой функции неотрицательна (неположительна) в этом интервале 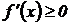 (
(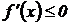 ).
).
Достаточное условие возрастания (убывания): Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого интервала, то функция возрастает (убывает) на этом интервале.
Функция f(x) в точке х1 имеет максимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x1)>f(x), при x ¹x1.
Функция f(x) в точке х1 имеет минимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x1)<f(x), при x ¹x1.
Экстремум функции называют локальным экстремумом, так как понятие экстремума связано лишь с достаточно малой окрестностью точки х1. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой. Наличие максимума или минимума в отдельной точке интервала не означает, что в этой точке функция f(x) принимает наибольшее или наименьшее значение на этом интервале.
Необходимое условие экстремума: В точке экстремума дифференцируемой функции ее производная равна нулю.
Достаточное условие экстремума: Если производная дифференцируемой функция в некоторой точке х0 равна нулю и меняет свой знак при переходе через это значение, то число f(х0) является экстремумом функции, причем если изменение знака происходит с плюса на минус, то максимум, если с минуса на плюс, то минимум.
Точки, в которых производная непрерывной функции равна нулю или не существует называются критическими.
Исследовать функцию на экстремум означает найти все ее экстремумы. Правило исследования функции на экстремум:
1). Найти критические точки функции у = f(x) и выбрать из них лишь те, которые являются внутренними точками области определения функции;
2). Исследовать знак производной f'(x) слева и справа от каждой из выбранных критических точек;
3). На основании достаточного условия экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них.
Для того чтобы найти наибольшее и наименьшее значение функции на отрезке необходимо выполнить несколько этапов:
1). Найти критические токи функции, решив уравнение f’(x)=0.
2). Если критические точки попали на отрезок, то необходимо найти значения в критических точках и на границах интервала. Если критические точки не попали на отрезок (или их не существует), то находят значения функции только на границах отрезка.
3). Из полученных значений функции выбирают наибольшее и наименьшее и записывают ответ, например, в виде: 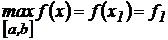 ;
; 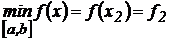 .
.
Решение задач
Пример 2.1. Найти дифференциал функции: 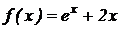 .
.
Решение. На основании свойства 2 дифференциала функции и определения дифференциала имеем:
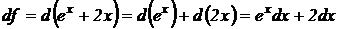 .
.
Пример 2.2. Найти дифференциал функции: 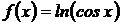
Решение. Функцию можно записать в виде: 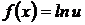 ,
, 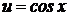 . Тогда имеем:
. Тогда имеем:
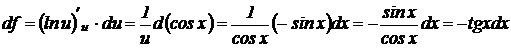
Пример 2.3. Найти вторую производную функции: 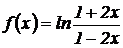
Решение. Преобразуем функцию 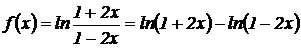 .
.
Найдем первую производную: 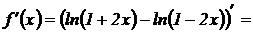
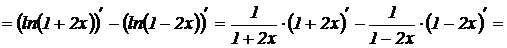
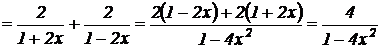 ;
;
найдем вторую производную:
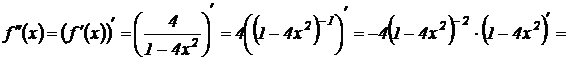
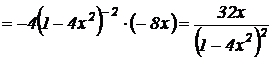 .
.
Пример 2.4. Найти дифференциал второго порядка от функции 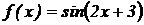 .
.
Решение. Найдем дифференциал второго порядка на основании выражения для вычисления 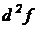 :
:
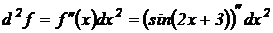 . Найдем сначала первую производную:
. Найдем сначала первую производную:
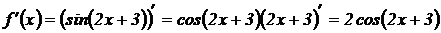 ; найдем вторую производную:
; найдем вторую производную: 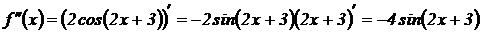 .
.
Тогда 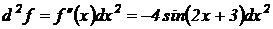 .
.
Пример 2.5. Найти угловой коэффициент касательной к кривой 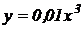 , проведенной в точке с абсциссой х=2.
, проведенной в точке с абсциссой х=2.
Решение. На основании геометрического смысла производной имеем, что угловой коэффициент равен производной функции в точке, абсцисса которой равна х. Найдем 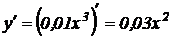 .
.
Вычислим 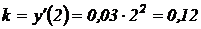 – угловой коэффициент касательной к графику функции.
– угловой коэффициент касательной к графику функции.
Пример 2.6. Популяция бактерий в момент времени t (t измеряется в часах) насчитывает 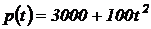 особей. Найти скорость роста бактерий. Найти скорость роста бактерий в момент времени t = 5 часов.
особей. Найти скорость роста бактерий. Найти скорость роста бактерий в момент времени t = 5 часов.
Решение. Скорость роста популяции бактерий – это первая производная 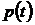 по времени t:
по времени t: 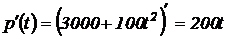 .
.
Если t = 5 часов, то 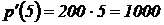 . Следовательно, скорость роста бактерий составит 1000 особей в час.
. Следовательно, скорость роста бактерий составит 1000 особей в час.
Пример 2.7. Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, уменьшении температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенной дозы лекарства. Если х обозначает дозу назначенного лекарства, а степень реакции у описывается функцией 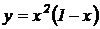 . При каком значении х реакция максимальна?
. При каком значении х реакция максимальна?
Решение. Найдем производную 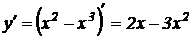 .
.
Найдем критические точки: 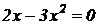 ⇒
⇒ 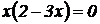 . ⇒ Следовательно, имеем две критические точки:
. ⇒ Следовательно, имеем две критические точки: 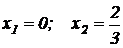 . Значение
. Значение 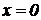 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Найдем вторую производную 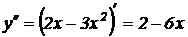 . Вычислим значение второй производной при
. Вычислим значение второй производной при 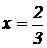 .
. 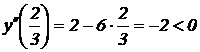 . Значит,
. Значит, 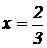 – уровень дозы, который дает максимальную реакцию.
– уровень дозы, который дает максимальную реакцию.
Примеры для самостоятельного решения
Найти дифференциал функции:
1. 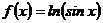 .
.
2. 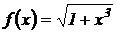 .
.
3. 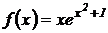 .
.
4. 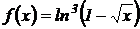
Найти вторые производные следующих функций:
5. 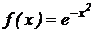 .
.
6. 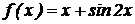 .
.
7. 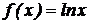 .
.
8. 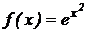 .
.
Найти производные второго порядка и записать дифференциалы второго порядка для следующих функции:
9. 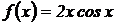 .
.
10. 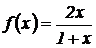 .
.
11. Исследовать функцию на экстремум 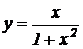 .
.
12. Найти наибольшее и наименьшее значения функции 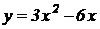 на отрезке
на отрезке 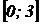 .
.
13. Найти интервалы возрастания и убывания функции, точки максимума и минимума и точки пересечения с осями: 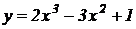
14. Закон движения точки имеет вид 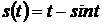 . Определить закон скорость и ускорение этой точки.
. Определить закон скорость и ускорение этой точки.
15. Уравнение движения точки имеет вид 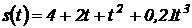 (м). Найти 1) положение точки в моменты времени
(м). Найти 1) положение точки в моменты времени 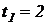 с и
с и 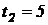 с; 2) среднюю скорость за время, прошедшее между этими моментами времени; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
с; 2) среднюю скорость за время, прошедшее между этими моментами времени; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
Задание на дом.
Практика:
Найти дифференциал функции:
1. 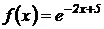 ;
;
2. 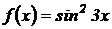 ;
;
Найти производные второго порядка функции:
3. 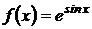 .
.
4. 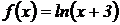
5. 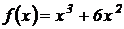
Найти дифференциалы второго порядка
6. 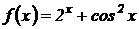 .
.
7. Точка движется прямолинейно по закону 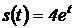 . Вычислить скорость и ускорение в моменты времени
. Вычислить скорость и ускорение в моменты времени 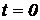 и
и 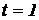 .
.
Найти интервалы возрастания и убывания функций:
8. 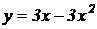 .
.
9. 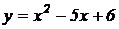 .
.
10. При вливании глюкозы ее содержание в крови человека, выраженное в соответствующих единицах, спустя t часов составит 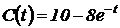 . Найдите скорость изменения содержания глюкозы в крови при а) t =1 ч; б) t =2 ч.
. Найдите скорость изменения содержания глюкозы в крови при а) t =1 ч; б) t =2 ч.
Теория.
1. Лекция по теме «Производные и дифференциалы функции нескольких аргументов. Приложение дифференциала функции нескольких аргументов».
2. Занятие 3 данного методического пособия.
3. Павлушков И.В. и другие стр. 101-113, 118-121.
Занятие 3. Производные и дифференциалы функции нескольких аргументов
Актуальность темы: данный раздел математики имеет широкое применение при решении ряда прикладных задач, так как многим явлениям физического, биологического, химического явления присуща зависимость не от одной, а от нескольких переменных (факторов).
Цель занятия: научиться находить частные производные и дифференциалы функций нескольких переменных.
Целевые задачи:
знать: понятие функции двух переменных; понятие частных производных функции двух переменных; понятие полного и частных дифференциалов функции нескольких переменных;
уметь: находить производные и дифференциалы функций нескольких переменных.
Краткие сведения из теоретического курса
Основные понятия
Переменная z называется функцией двух аргументов x и y, если некоторым парам значений 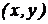 по какому-либо правилу или закону ставится в соответствие определенное значение z. Функция двух аргументов обозначается
по какому-либо правилу или закону ставится в соответствие определенное значение z. Функция двух аргументов обозначается 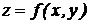 .
.
Функция 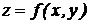 задается в виде поверхности в прямоугольной системе координат в пространстве. Графиком функции двух переменных
задается в виде поверхности в прямоугольной системе координат в пространстве. Графиком функции двух переменных 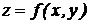 называется множество точек трехмерного пространства (x, y, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением
называется множество точек трехмерного пространства (x, y, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением 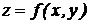 .
.
Рассмотрим функцию z=f(x,y). Дадим аргументу х приращение Dх, а аргументу у – приращение Dу. Тогда функция z получит наращенное значение 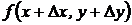 .
.
Величина 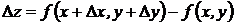 называется полным приращением функции в точке
называется полным приращением функции в точке 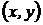 . Частным приращением по переменной х называется величина:
. Частным приращением по переменной х называется величина: 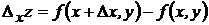 . Аналогично определяется частное приращение по переменной у:
. Аналогично определяется частное приращение по переменной у: 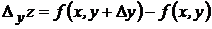 .
.
Частные производные и дифференциалы функции
нескольких переменных
Частной производной от функции 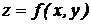 по независимой переменной х называют конечный предел
по независимой переменной х называют конечный предел 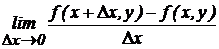 , вычисленный при постоянном у. Обозначается:
, вычисленный при постоянном у. Обозначается: 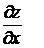 или
или 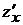 .
.
Частной производной от функции 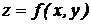 по независимой переменной у называют конечный предел
по независимой переменной у называют конечный предел 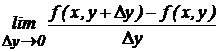 , вычисленный при постоянном х. Обозначается:
, вычисленный при постоянном х. Обозначается: 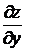 или
или 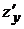 .
.
Пусть функция z=f(x,y) имеет две непрерывные частные производные 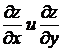 .
.
Произведение 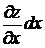 называется частным дифференциалом функции z=f(x,y) по х и обозначаются
называется частным дифференциалом функции z=f(x,y) по х и обозначаются 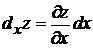 .
.
Произведение 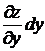 называется частным дифференциалом функции z=f(x,y)по х и обозначаются
называется частным дифференциалом функции z=f(x,y)по х и обозначаются 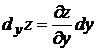 .
.
Полный дифференциал функции
Дифференциалом функции называется сумма произведений частных производных этой функции на приращение соответствующих независимых переменных, т. е. 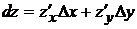 . Так как
. Так как 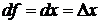 и
и 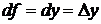 тогда можно записать:
тогда можно записать: 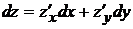 или
или 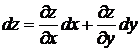 .
.

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!