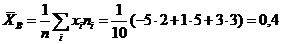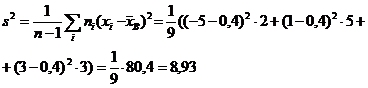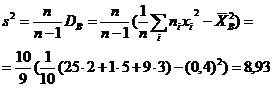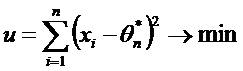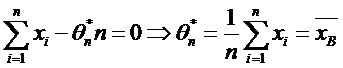Алгеброй множествS называется такая система подмножеств универсального множества W, что
1) WÎ S, ØÎ S
2) " A, B Î S Þ A+B Î S, AB Î S, A\B Î S.
σ-алгеброй множествS называется такая система подмножеств универсального множества W, что
1) WÎ S, ØÎ S
2) " A, B: A\B Î S.
3) A1, A2, …An, … Î S Þ (A1 +A2+ …+An+ …) Î S,
(A1A2 …An, …) ÎS,
Аксиомы теории вероятностей
Вероятностным пространством называется тройка
(W, S, P), где
W – универсальноемножество
S – егоσ-алгебра
P – функция из S в множество действительных чисел, удовлетворяющая свойствам
1) P(A) ≥ 0; Всякому событию из поля события ставят в соответствие некоторое неотрицательное число, которое называют его вероятностью
2) P(W) = 1; Вероятность достоверного события принимается равной единице
3) Если A1, A2, …An, … не пересекаются, то
P(A1 +A2+ …+An+ …) = P(A1) + P(A2) + …+P(An)+ … (аксиома сложения).
Вероятность суммы двух несовместных событий равна сумме вероятностей каждого
Аксиома 4. Если событие А равносильно наступлению хотя бы одного из попарно несовместных событий А1, А2, …,Аn, то вероятность этого события равна сумме вероятностей каждого  . .
|
Следствия:
1. Вероятность противоположного события равна 1 за вычетом вероятности прямого события
 ;
;
Доказательство 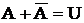 ;
;
 .
.
2. Вероятность невозможных событий равна 0

Доказательство
 .
.
3. Вероятность любого события лежит в пределах
0 <= Р(Аi) <= 1.
2. Классическая и геометрическая вероятности. Определение (интерпретация аксиом), примеры.
Классическая вероятность
Пространство W состоит из конечного числа равновероятных элементарных событий Е1, Е2,...,Еn.
Элементарное событие называется благоприятным событию А, если его появление влечет появление события А. Пусть m - число благоприятных для А элементарных событий, n - число всех элементарных событий. Тогда

Действительно, Р(Е1+Е2+...+Еn)=Р(W)=1, так как события несовместны, то
Р(Е1) + Р(Е2) +...+ Р(Еn) =1 (1).
По условию события равновозможные, следовательно,
Р(Е1) = Р(Е2) =...= Р(Еn) (2).
Из равенств (1) и (2) следует, что Р(Е1)=Р(Е2) =…
=Р(Еn) =
Найдем
Р(А) = Р(Е1 + Е2 +... + Еm) = Р(Е1)+Р(Е2)+...+Р(Еm) =m/n
Пример:
Опыт - бросание игральной кости
Событие А - выпадение числа очков, кратного 3.
Найдем вероятность события А.
Решение:
Всего случаев 6. Благоприятных из них 2, следовательно, 
Геометрическая вероятность
Пространство W является ограниченной и измеримой областью в Rn. Сигма-алгебра пространства есть совокупность всех измеримых подмножеств области W.
Вероятность события А (вероятность попадания точки в множество А) пропорциональна его мере как множества
и не зависит от его расположения и формы.
Если мера всей области равна S, а мера части D области, попадание в которую благоприятствует появлению события А, равна SD, то вероятность события А равна.
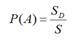

Геометрическая вероятность
На практике часто встречаются испытания, число возможных исходов которых бесконечно.
Два студента условились встретиться в определенном месте между 18 и 19 часами. Пришедший первым ждет 15 мин и уходит. Определить вероятность встречи, если время прихода каждого независимо и равновозможно в течение указанного часа.
Решение примера 6:
Пусть х- время прихода одного студента, у- время прихода второго. Чтобы встреча состоялась, необходимо и достаточно, чтобы êх - у ê£ 15,
т.е. -15 £ x - y £ 15. Область возможных значений - квадрат со стороной, равной 60. 4

Область D – часть квадрата между прямыми
х – у = – 15 и х – у = 15. Следовательно,


Элементы комбинаторики
Имеется совокупность n объектов, назовем ее генеральной совокупностью. Из генеральной совокупности наудачу отбираем m объектов, эту отобранную совокупность назовем выборкой.
Выборка может быть упорядоченной, если порядок объектов (элементов) играет роль, и может быть неупорядоченной, если порядок элементов роли не играет.
Выборка может быть без повторений, если элементы повторяться не могут, и может быть с повторениями, если элементы в выборке повторяются.
Например, телефонный номер 60-61-51 – упорядоченная выборка с повторениями из десяти цифр по шести.
Упорядоченная выборка из n элементов по m называется размещением, неупорядоченная выборка из n элементов по m называется сочетанием. Число размещений и сочетаний c повторениями и без повторений из n элементов по m можно найти:
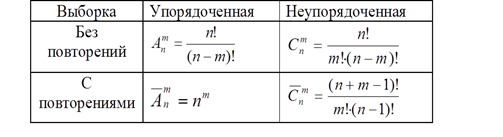
Два счета из десяти выполнены с ошибками. Найти вероятность того, что из четырех взятых на проверку счетов один счет окажется с ошибками
Решение:
Имеем дело с неупорядоченными выборками без повторений, следовательно, всего случаев n=С104,
благоприятных из них m=С21×С83.
Следовательно 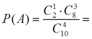
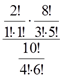 =
= 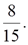
Выборка без возвращения
состоит в том, что мы наугад вынимаем последовательно из урны n шаров, не возвращая их обратно.
Какова вероятность вытащить ровно m белых шаров?
Элементарные события – последовательности различных шаров.
Всего элементарных событий 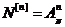
Из них успешных 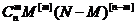
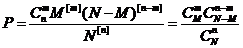
Выборка с возвращением
состоит в том, что мы наугад вынимаем последовательно из урны n шаров, каждый раз фиксируя выбранный шар и возвращаю его в урну.
Какова вероятность вытащить ровно m белых шаров?
Выборка с возвращением
Элементарные события – последовательности шаров.
Всего элементарных событий 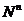
Из них успешных 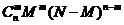
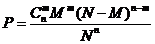
Следствие.
Если события А1, А2,...,Аnнесовместны,
то
Р(А1+А2+...+Аn)=P(A1)+P(A2)+...+P(An).
Доказательство
Воспользуемся методом математической индукции.
из определения Р(А1×А2)=Р(А1)×Р(А2|А1).
Предполагаем, что теорема верна для (n-1) событий; докажем, что она верна для n событий.
Найдем Р(А1×А2×А3×...×Аn)=P((A1×A2×A3×...×An-1)×An) = =P(A1×A2×A3×...×An-1)×P(An|A1×A2×A3×...×An-1) = / попредположению /= P(A1)×P(A2|A1)× P(A3|A1×A2) ×..×P(An-1| A1×A2×A3×An-2)×P(An|A1×A2×A3×...×An-1).g
Пример 8:
Два студента выполняют независимо друг от друга задание. Вероятность того, что задание будет выполнено первым студентом 0,6;
для второго студента эта вероятность равна 0,8.
Найти вероятность того, что
· оба студента выполнят задание;
· только один из них выполнит задание;
· хотя бы один из них выполнит задание.
Решение.
События: А – задание выполнит первый студент,
В- задание выполнит второй студент.
По условию Р(А) = р1 = 0,6; Р(В)=р2 = 0,8; следовательно, Р() = 1-p1 = q1 = 1-0,6 = 0,4; P() = 1-p2 = q2 = 1-0,8 = 0,2.
· Р(А×В) = /события А и В - независимые события / = Р(А)×Р(В) = р1×р2 =0,6×0,8 = 0,48.
·Р(А× + ×B) = / A× и ×B - несовместные события /= Р(А×) + Р(×В) = Р(А)×Р() +
Р()×Р(В) = p1×q2+q1×p2 = 0,6×0,2 + 0,4×0,8 = 0,44.
·P(A+B)=/ А и В-совместные события /= Р(А)+Р(В)-Р(А×В)=0,6+0,8-0,48=0,92
или т.к. А+В и противоположные события, то
Р(А+В)=1-Р()= 1 - Р()×Р() = 1-q1×q2 = 1-0,4×0,2 = 1-0,08 = 0,92.4
Пример 7:
Студент знает ответы на 20 из 25 вопросов. Какова вероятность того, что он ответит на два выбранных наудачу вопроса?
Решение.
Рассмотрим события:
А- студент знает ответ на первый вопрос,
В- студент знает ответ на второй вопрос.
 Найдем Р(А×В).
Найдем Р(А×В).
Р(А×В) = Р(А)×Р(В|А) =
Полная группа событий -несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно (и только ровно одно) из них. 
 называются гипотезами. называются гипотезами.

| |
7. Полная группа событий. Вывод формулы полной вероятности.
Теорема (формула полной вероятности)
Пусть в результате опыта может появиться какое-либо из несовместных событий Н1,Н2,...,Нn, образующих полную группу. Событие А может появиться только вместе с одним из этих событий.
 Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А|Нi), где i =, то
Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А|Нi), где i =, то
Доказательство.
Р(А)=Р(А× = =Р(А×(Н1+Н2+...+Нn)=P(A×H1+A×H2+...+A×Hn)=
/события A×Hi иA×Hj, где несовместные события, т.к. (A×Hi)×(A×Hj)=A×Hi×Hj=A×(Hi×Hj)=A× Ø = Ø
= Р (А × Н 1)+ Р (А × Н 2)+...+ Р (А × Нn)=
= P (H 1)× P (A | H 1)+ P (H 2)× P (A | H 2)+...+ P (Hn)×P(A | Hn).
Пример:
На стройку поступают блоки с трех баз, причем 50% с первой базы,30% со второй базы, остальные с третьей базы. Вероятность того, что блок c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу на стройке блок окажется бракованным.
Решение.
Рассмотрим гипотезы:
Н1 - взятый наудачу блок поступил с первой базы,
Н2 - взятый наудачу блок поступил со второй базы,
Н3 - взятый наудачу блок поступил с третьей базы.
Событие А - взятый наудачу на стройке блок окажется бракованным.
По условию Р(Н1)=50/100=0,5; Р(Н2)=30/100=0,3; Р(Н3)=(100-50-30)/100 = 0,2.Р(А|Н1)=0,09;
Р(А|Н2)=0,1; Р(А|Н3)=0,08.
Следовательно, по формуле полной вероятности
Р(А)=0,5×0,09+0,3×0,1+0,2×0,08=0,091.
Вопрос 11.
Независимые испытания. Полиномиальная схема.
Производится n независимых испытаний, в каждом из которых события А1, …, Аk наступают с вероятностями р1,…, рk (р1 + … + рk = 1).
Найти вероятность P (n1, …, nk) того, что в результате эксперимента событие А1 наступит n1 раз, …, событие Аk наступит nk раз.
Пример. Задача о байдарке.
При прохождении порога байдарка
- не получает повреждений с вероятностью 0,7;
- получает серьезное повреждение с вероятностью 0,2;
- полностью ломается с вероятностью 0,1.
Два серьезных повреждения приводят к поломке. Найти вероятность того, что байдарка преодолеет 10 порогов (т.е. не будет полностью сломана после 10 порогов).
Наивероятнейшее число наступлений события при повторении испытаний:
 Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события
Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события
по крайней мере не меньше вероятностей других событий при любом m.

Если m 0 – наивероятнейшее число появления события А в n независимых испытаниях, в каждом из которых событие А наступает с постоянной вероятностью р
np - q < m 0 < np + p.
Найти наивероятнейшее число отказавших элементов, если каждый из пяти независимо работающих элементов отказывает с вероятностью 0,4.
Решение.
Так как n=5, p=0,4, q=0,6, то 5×0,4-0,6£ m0 < 5×0,4+0,4
Или 1,4 < m0 < 2,4. Следовательно, m0=2
8. Теорема (формула Байеса) (теорема переоценки гипотез)
Пусть в условиях предыдущей теоремы (формула полной вероятности) событие А наступило и мы нашли вероятность Р(А). Спросим, как изменились вероятности гипотез в связи с появлением события А, т.е. найдем Р(Нi|А), где i=1,2,...,n.
По аксиоме:Р(А×Нi)=P(A)×P(Hi|A)=P(Hi)×P(A|Hi), откуда

В предыдущем примере событие А наступило, т.е. взятый наудачу на стройке блок оказался бракованным. Определить вероятность того, что этот блок поступил со второй базы.
На стройку поступают блоки с трех баз, причем 50% с первой базы,30% со второй базы, остальные с третьей базы. Вероятность того, что блок c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу на стройке блок окажется бракованным.
Решение.
Рассмотрим гипотезы:
Н1 - взятый наудачу блок поступил с первой базы,
Н2 - взятый наудачу блок поступил со второй базы,
Н3 - взятый наудачу блок поступил с третьей базы.
Событие А - взятый наудачу на стройке блок окажется бракованным.
Решение.
Р(Н2|А) = 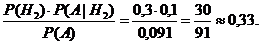
Полиномиальная схема.
Производится n независимых испытаний, в каждом из которых события А1, …, Аk наступают с вероятностями р1,…, рk (р1 + … + рk = 1).
Найти вероятность P(n1, …, nk) того, что в результате эксперимента событие А1 наступит n1 раз, …, событие Аk наступит nk раз.
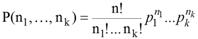
Пример. Задача о байдарке.
Пример. Вероятность ошибки в каждом из ста счетов равна 0,2.Найти
· вероятность того, что ошибки имеются в 20 счетах;
· вероятность того, что число счетов с ошибками заключено между
числами m1=20 и m2=30.
Решение.
· n=100, m=20, p=0,2, q=0,8, npq=100×0,2×0,8=16

Пример. Задача о поезде.
В поселке 2500 жителей. Каждый из них примерно 6 раз в месяц ездит на поезде в город, выбирая дни поездок по случайным мотивам независимо от остальных. Какой наименьшей вместимостью должен обладать поезд, чтобы он переполнялся в среднем не чаще одного раза в 100 дней (поезд ходит один раз в сутки).

F(x)- неубывающая функция.
Замечание
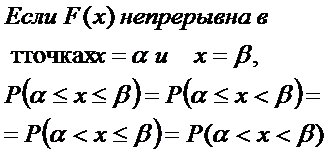
Функция распределения случайной величины ξ
F(x)= 
Найти вероятность попадания случайной величины ξ в интервал (1;6).
Решение Р(1<ξ<6)=F(6)-F(1)=0,2(6-3)-0=0,6.4
Свойства дисперсии
1. D(C) = 0
2. D(kξ) = k2D(ξ)
3. D(ξ) = M(ξ2) – [M(ξ)]2

Пример:
D(ξ) = 13,61 
D(η) = 4,17 
Биномиальное распределение
Биномиальным распределением называется распределение дискретной случайной величины ξ = m, для которой ряд распределения задается формулой Бернулли

где m =0;1;2;..., n и q =1– p.
Биномиальное распределение имеет дискретная случайная величина ξ – число появлений события А в n независимых испытаниях, если вероятность появления события А в каждом испытании постоянна и равна р, и, следовательно, вероятность непоявления события А в каждом испытании равна q =1– p.
Пример. База отправила в магазин 500 изделий, веро-ятность повреждения изделия в пути 0,002. Найти веро-ятность того, что в пути будут повреждены 5 изделий.
Решение.
По условию n=500, p=0,002, m=5, следовательно, a =np= =500×0,002=1, тогда
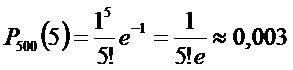
25. Двумерная дискретная случайная величина, вид закона распределения, условие нормировки, распределения составляющих величин, пример.
Пример. Дано распределение двумерной случайной величины
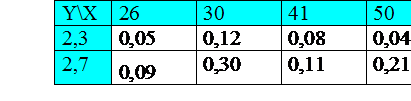
Найти законы распределения составляющих случайных величин ξ и η.
Решение.
Действительно,
Р(ξ=26)=Р(ξ=26; η =2,3)+Р(ξ=26; η =2,7)=0,05+0,09=0,14;
Р(ξ=30)=Р(ξ=30; η =2,3)+Р(ξ=30; η =2,7)=0,12+0,30=0,42;
аналогично найдите Р(ξ=41) и Р(ξ=50).
 Аналогично находим
Аналогично находим
Действительно,
P(η=2,3)=P(ξ=26;η=2,3)+P(ξ=30;η=2,3)+P(ξ=41;η=2,3)+P(ξ=50;η=2,3)=0,05+ 0,12+0,08+0,04=0,29;
аналогично найдите Р(η =2,7).
(Проверьте выполнение условия нормировки в каждом распределении).4
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большое рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше.
Пример:Из генеральной совокупности извлечена выборка

Найти:
· выборочные моду,
· медиану,
· коэффициент вариации.
Решение.
· Наибольшую частоту 7 имеет варианта х = 3, следовательно, Mо = 3.
· Т. к. объем выборки n=20, т. е. число вариант четно, то

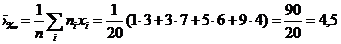
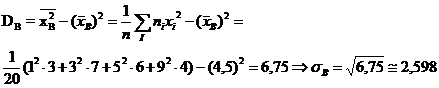
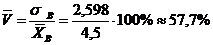
29. Равномерное непрерывное распределение, функция распределения и плотность, вывод математического ожидания и дисперсии.
Непрерывная случайная величина ξ имеет равномерное распределение, если на промежутке, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение, т.е.
 Из условия нормировки непрерывной случайной величины следует
Из условия нормировки непрерывной случайной величины следует
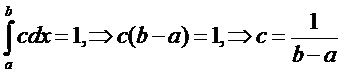 Таким образом
Таким образом
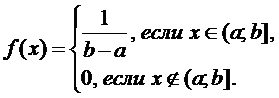
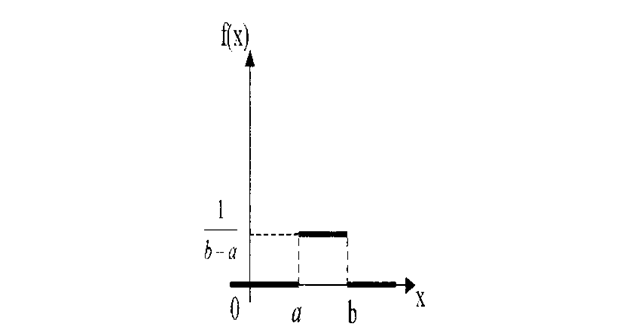
Пример. Цена деления шкалы измерительного прибора равна 0,1. Показания прибора округляют до ближайшего деления. Найти вероятность того, что при вычислении будет сделана ошибка, меньшая 0,02.
Решение.
Ошибку округления при вычислении рассматриваем как непрерывную случайную величину ξ, имеющую равномерное распределение, причем


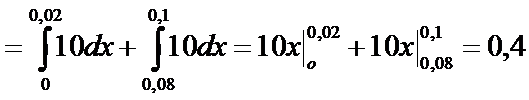
Правило трех сигм
Если задана t = 3, то
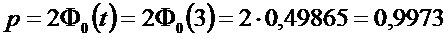
Итак,
P (а- 3s<ξ<а+3s)=0,9973,
т.е. практически все значения случайной величины находятся в интервале (а- 3s; а+3s). Вероятность же того, что значения случайной величины попадут вне этого интервала пренебрежимо мала и равна 0,0027.
Пример. Ошибка измерения подчинена нормальному закону с параметрами а =5м, s=10м. Найти вероятность того, что измеренное значение расстояния будет отклоняться от истинного не более, чем на 15м.
Решение.
Случайная величина ξ-ошибка измерения,
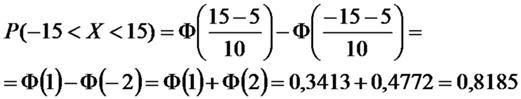
3Пример. На станке изготовляются втулки, длина которых L представляет нормально распределенную случайную величину, причем М [ L ] = 20cм, s = 0,2 см.
Найти:
· Вероятность того, что длина втулки будет отклоняться от ее среднего значения на величину, меньшую 0,3см.
· Длину втулки с вероятностью 0,95.
· Длину втулки с вероятностью 0,9973.
Решение.
• По условию а=20см, s=0,2 см.
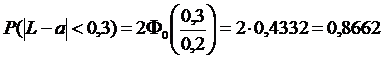
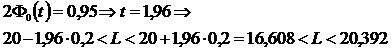
• так как по условию р = 0,9973, то
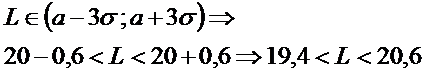
Решение.
Т.к. P(η=1)=P(ξ=1)=0,3;
P(η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то

2. ξ - непрерывная случайная величина, т.е. известна плотность распределения случайной величины fξ(x). Пусть функция y=g(x) - непрерывна, монотонна и дифференцируема на всем интервале возможных значений случайной величины ξ. Тогда существует обратная функция х = g-1(у), также непрерывная, монотонная и дифференцируемая. Тогда плотность вероятности случайной величины η=g(ξ) равна
fη(x) = fξ(g-1(у))×|[g-1(у)]/|.
Замечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f η i(y) для каждого интервала, а затем
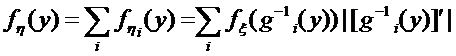
Решение.
Т.к. P(η=1)=P(ξ=1)=0,3;
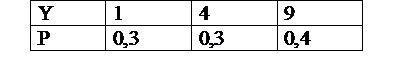 P(η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то
P(η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то
ξ - непрерывная случайная величина, т.е. известна плотность распределения случайной величины fξ(x). Пусть функция y=g(x) - непрерывна, монотонна и дифференцируема на всем интервале возможных значений случайной величины ξ. Тогда существует обратная функция х = g-1(у), также непрерывная, монотонная и дифференцируемая. Тогда плотность вероятности случайной величины η=g(ξ) равна
fη(x) = fξ(g-1(у))×|[g-1(у)]/|.
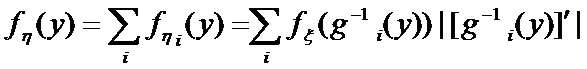 Замечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f η i(y) для каждого интервала, а затем
Замечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f η i(y) для каждого интервала, а затем
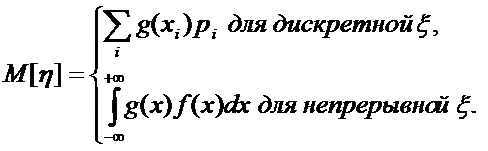 Числовые характеристики функций случайного аргумента
Числовые характеристики функций случайного аргумента
В этом случае
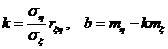
Уравнения регрессии
Т.к. М[ξ | η = y ] меняется с изменением значения у, то можно рассматривать функцию
m ξ(y)=М[ξ | η= y ],
Виды выборок
Повторная выборка – отобранный объект после обследования возвращается в совокупность перед отбором следующего объекта.
Бесповторная выборка – отобранный объект не возвращается в совокупность при обследовании.
(На практике обычно пользуются бесповторными выборками)
Репрезентативная (представительная) – дает правильное представление о совокупности,
(насколько это позволяют имеющиеся деньги и время)
Ошибочно сформированная выборка даст искаженное представление о совокупности.
В силу закона больших чисел можно утверждать, что выборка будет представительной,
· если ее объем достаточно велик, а ее значения независимы;
· если ее осуществлять случайно и если все ее объекты имеют одинаковую вероятность попасть в выборку.
(Если объем совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторными и бесповторными выборками практически исчезает)
Полигон и гистограмма
Полигоном частот выборки называется ломаная, соединяющая точки (х1;n1), (x2; n2),..., (xк;nк).
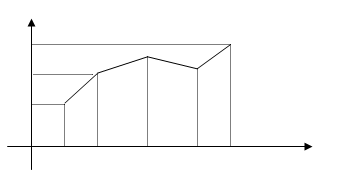
Полигоном относительных частот называется ломаная, соединяющая точки (х1; W1), (х2; W2),..., (хк; Wк).
Гистограмма частот – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длины hi, а высоты равны  (плотность частоты).
(плотность частоты).

Групповая и общая средние
Допустим, что некоторая совокупность разбита на несколько непересекающихся групп, необязательно одинаковых по объему. Группы называются непересекающимися, если каждый член совокупности принадлежит только одной группе. Рассматривая каждую группу как самостоятельную совокупность, можно найти их среднюю арифметическую.
Пример. Вычислить среднее число жителей в поселках городского типа по данным таблицы
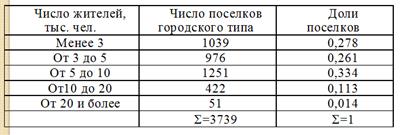
 (2×1039 + 4×976 +7,5×1251 + 15×422 + 25×51)/3739=6,14 (тыс. чел.)3
(2×1039 + 4×976 +7,5×1251 + 15×422 + 25×51)/3739=6,14 (тыс. чел.)3
Пример.Распределение рабочих предприятия по заработной плате и по цехам приведено в таблице. Найти среднюю зарплату.

Решение.1 способ

Оценка дисперсии
В качестве оценки D ξ можно взять распределения выборочную дисперсию

Можно доказать, что выборочная дисперсия является состоятельной и смещенной оценкой генеральной дисперсии D ξ,причем,

т.е. эта оценка занижает в среднем истинное значение дисперсии на D ξ /n. Правда это смещение сходит на нет при n ®¥.
С целью исправления смещения вводят несмещенную оценку Dξ, которой является исправленная выборочная дисперсия

Действительно

Так как  , то оценка s 2 является несмещенной.
, то оценка s 2 является несмещенной.
Итак 
Стандартно вводятся выборочное среднее квадратическое отклонение 
и исправленное среднее квадратическое отклонение 
Замечания:
· На практике пользуются исправленной дисперсией, если n £30.
· Если, xi – варианта выборки, ni – ее частота и n – объем выборки, то


· Для вычисления DВ удобнее применять формулу

· Выборочное sв и исправленное s (средние квадратические отклонения) – смещенные оценки s.
· Пример. Из генеральной совокупности извлечена выборка

Решение.
Объем выборки n = 2 + 5 + 3 = 10,
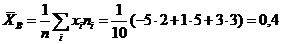
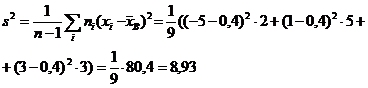
Или
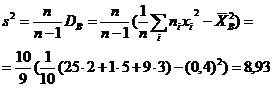
40) Интервальные оценки, доверительный интервал, вывод доверительного интервала для параметра a нормальной случайной величины нормального распределения при известном σ
Метод наименьших квадратов
Пример: Найти оценку МНК для генеральной средней
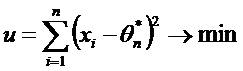
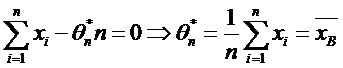
Алгеброй множествS называется такая система подмножеств универсального множества W, что
1) WÎ S, ØÎ S
2) " A, B Î S Þ A+B Î S, AB Î S, A\B Î S.
σ-алгеброй множествS называется такая система подмножеств универсального множества W, что
1) WÎ S, ØÎ S
2) " A, B: A\B Î S.
3) A1, A2, …An, … Î S Þ (A1 +A2+ …+An+ …) Î S,
(A1A2 …An, …) ÎS,
Аксиомы теории вероятностей



 .
.
 ;
;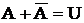 ;
; .
.
 .
.



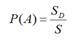




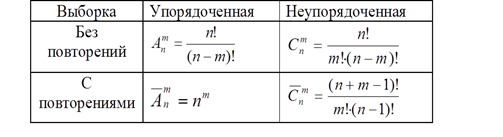
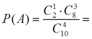
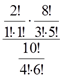 =
= 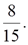
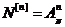
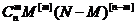
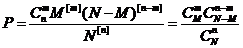
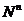
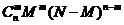
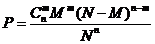
 Найдем Р(А×В).
Найдем Р(А×В).
 называются гипотезами.
называются гипотезами.


 Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А|Нi), где i =, то
Если известны вероятности гипотез Р(Нi) и условные вероятности Р(А|Нi), где i =, то
 Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события
Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события

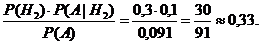
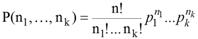


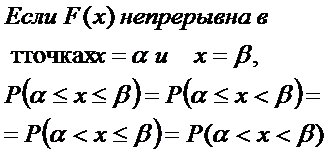





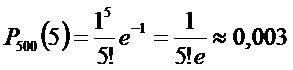
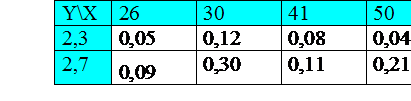
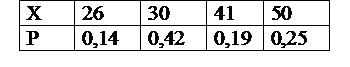
 Аналогично находим
Аналогично находим

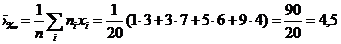
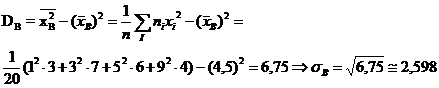
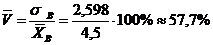
 Из условия нормировки непрерывной случайной величины следует
Из условия нормировки непрерывной случайной величины следует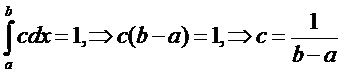 Таким образом
Таким образом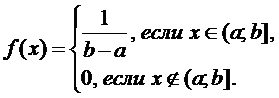



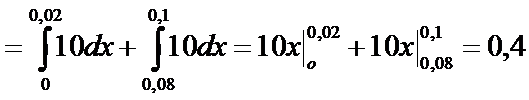
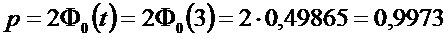
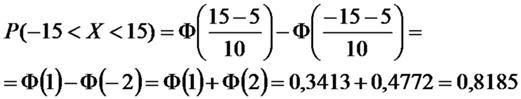
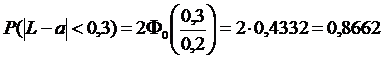
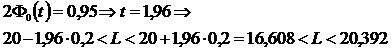
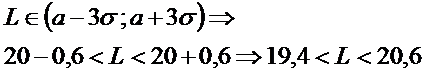

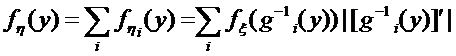
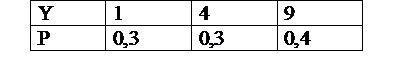 P(η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то
P(η=4)=P(ξ= -2)+P(ξ=2)=0,1+0,2=0,3; P(η=9)=P(ξ=3)=0,4; то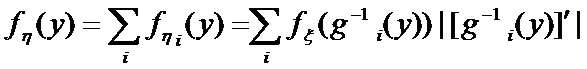 Замечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f η i(y) для каждого интервала, а затем
Замечание: Если y=g(x) - немонотонна, то следует весь интервал возможных значений случайной величины ξ разбить на такие интервалы, в которых функция g (x) монотонна, и найти плотности вероятности f η i(y) для каждого интервала, а затем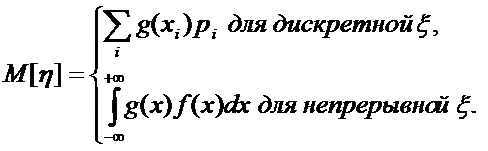 Числовые характеристики функций случайного аргумента
Числовые характеристики функций случайного аргумента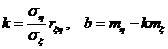

 (плотность частоты).
(плотность частоты).

 (2×1039 + 4×976 +7,5×1251 + 15×422 + 25×51)/3739=6,14 (тыс. чел.)3
(2×1039 + 4×976 +7,5×1251 + 15×422 + 25×51)/3739=6,14 (тыс. чел.)3





 , то оценка s 2 является несмещенной.
, то оценка s 2 является несмещенной.