10. Пусть функция 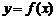 определена и непрерывна в окрестности точки
определена и непрерывна в окрестности точки 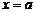 . Если независимой переменной х придать приращение D х в этой точке, то функция получит соответствующее приращение
. Если независимой переменной х придать приращение D х в этой точке, то функция получит соответствующее приращение  . Если D х ®0, то, по определению непрерывной в точке
. Если D х ®0, то, по определению непрерывной в точке 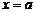 функции, и D у ®0.
функции, и D у ®0.
С целью исследования скорости изменения значений функции вводится понятие производной.
Производной функции 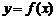 в точке
в точке 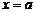 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю.
называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю.
Для обозначения производной используются символы:  . Таким образом, по определению
. Таким образом, по определению
 . (1)
. (1)
Операцию нахождения производной называют дифференцированием.
Если функция 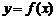 имеет производную
имеет производную 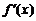 в каждой точке
в каждой точке  , то производную
, то производную 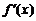 можно рассматривать как функцию переменной х на множестве X.
можно рассматривать как функцию переменной х на множестве X.
Cуществуют односторонние пределы:  и
и  , не равные между собой. Такимобразом, производная функции
, не равные между собой. Такимобразом, производная функции  в точке
в точке 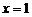 не существует. □
не существует. □
Учитывая, что существуют вышеуказанные односторонние пределы, в этом случае говорят, что у рассматриваемой функции существуют односторонние производные в точке 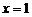 (правая и левая соответственно).
(правая и левая соответственно).
Выясним связь между существованием производной и непрерывностью функции в заданной точке.
Функция может быть непрерывной в точке, но не иметь в ней производной
 20. Геометрический смысл производной. Пусть функция
20. Геометрический смысл производной. Пусть функция 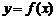 определена на интервале
определена на интервале  . Предположим, что кривая АВ является графиком этой функции (рис. 1). Пусть
. Предположим, что кривая АВ является графиком этой функции (рис. 1). Пусть  – произвольная точка графика. Придадим аргументу
– произвольная точка графика. Придадим аргументу 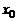 приращение D х. Соответствующую точку на графике обозначим через
приращение D х. Соответствующую точку на графике обозначим через  .
.
Через точки М и Р проведем секущую. Найдем угловой коэффициент секущей, проходящей через точки М и Р. Ясно, что он вычисляется по формуле (см. рис. 1)  Если точку Р устремить по кривой АВ к точке М, то положение секущей будет, вообще говоря, изменяться.
Если точку Р устремить по кривой АВ к точке М, то положение секущей будет, вообще говоря, изменяться.
Если при 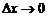 существует предельное положение секущей, то полученная прямая называется касательной к графику
существует предельное положение секущей, то полученная прямая называется касательной к графику 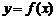 в точке
в точке 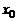 . Понятно, что условием существования предельного положения секущей является существование следующего предела:
. Понятно, что условием существования предельного положения секущей является существование следующего предела:
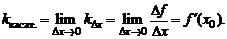
Итак, график функции 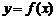 имеет касательную в точке
имеет касательную в точке 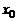 тогда и только тогда, когда функция дифференцируема в точке
тогда и только тогда, когда функция дифференцируема в точке 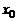 и
и  является угловым коэффициентом касательной.
является угловым коэффициентом касательной.
Составим теперь уравнение касательной в точке 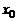 как уравнение прямой, проходящей через точку
как уравнение прямой, проходящей через точку  ,
,  , имеющей угловой коэффициент, равный
, имеющей угловой коэффициент, равный  :
:
 (2)
(2)
Прямая, проходящая через точку  и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Учитывая условие перпендикулярности двух прямых, запишем уравнение нормали:
и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Учитывая условие перпендикулярности двух прямых, запишем уравнение нормали:
 (полагаем, что
(полагаем, что  ).
).
Если 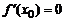 , то нормалью будет прямая
, то нормалью будет прямая 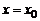 .
.
30. Физический смысл производной. Пусть некоторая материальная точка М движется прямолинейно и задан закон ее движения  ,т.е. известно расстояние s (t) от точки М до некоторой начальной точки отсчета в каждый момент времени t. В момент времени
,т.е. известно расстояние s (t) от точки М до некоторой начальной точки отсчета в каждый момент времени t. В момент времени  точка пройдет расстояние
точка пройдет расстояние  , а в момент времени
, а в момент времени  – расстояние
– расстояние  . За промежуток времени
. За промежуток времени  точка М пройдет расстояние
точка М пройдет расстояние 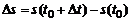 .
.
Отношение  можно рассматривать как среднюю скорость движения на промежутке времени
можно рассматривать как среднюю скорость движения на промежутке времени  . Чем меньше промежуток времени
. Чем меньше промежуток времени  , тем точнее соответствующая средняя скорость будет характеризовать движение точки в момент времени
, тем точнее соответствующая средняя скорость будет характеризовать движение точки в момент времени  . Поэтому предел средней скорости движения при
. Поэтому предел средней скорости движения при  называют скоростью движения (или мгновенной скоростью движения) точки М в момент времени
называют скоростью движения (или мгновенной скоростью движения) точки М в момент времени  и обозначают
и обозначают  , т.е.
, т.е.
 .
.
Но выражение справа есть  . Таким образом,
. Таким образом,  , т.е. скорость движения в момент времени
, т.е. скорость движения в момент времени  есть производная от пройденного пути по времени.
есть производная от пройденного пути по времени.
Понятие скорости, заимствованное из механики, удобно использовать и при изучении произвольной функции. Какую бы зависимость не отражала функция 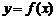 , отношение
, отношение 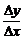 есть средняя скорость изменения зависимой переменной y относительно аргумента x, а
есть средняя скорость изменения зависимой переменной y относительно аргумента x, а  есть скорость изменения y в точке x.
есть скорость изменения y в точке x.
43. Правила дифференцирования, производная сложной и обратной функции. Производные элементарных функций.
431. Правила дифференцирования, производная сложной и обратной функции.
Если функции  и
и  имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что
имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что  ) и справедливы следующие формулы:
) и справедливы следующие формулы:
 ,
, 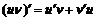 ,
, 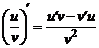 . (1)
. (1)
Производная обратной функции.
Утверждение 1. Если функция 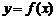 строго монотонна и непрерывна в некоторой окрестности точки
строго монотонна и непрерывна в некоторой окрестности точки 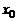 , имеет производную в точке
, имеет производную в точке 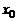 и
и  , то обратная функция
, то обратная функция  имеет производную в соответствующей точке
имеет производную в соответствующей точке  ,
,  , причем
, причем  .
.



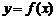 определена и непрерывна в окрестности точки
определена и непрерывна в окрестности точки 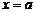 . Если независимой переменной х придать приращение D х в этой точке, то функция получит соответствующее приращение
. Если независимой переменной х придать приращение D х в этой точке, то функция получит соответствующее приращение  . Если D х ®0, то, по определению непрерывной в точке
. Если D х ®0, то, по определению непрерывной в точке  . Таким образом, по определению
. Таким образом, по определению . (1)
. (1)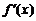 в каждой точке
в каждой точке  , то производную
, то производную  и
и  , не равные между собой. Такимобразом, производная функции
, не равные между собой. Такимобразом, производная функции  в точке
в точке 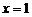 не существует. □
не существует. □ 20. Геометрический смысл производной. Пусть функция
20. Геометрический смысл производной. Пусть функция  . Предположим, что кривая АВ является графиком этой функции (рис. 1). Пусть
. Предположим, что кривая АВ является графиком этой функции (рис. 1). Пусть  – произвольная точка графика. Придадим аргументу
– произвольная точка графика. Придадим аргументу 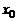 приращение D х. Соответствующую точку на графике обозначим через
приращение D х. Соответствующую точку на графике обозначим через  .
. Если точку Р устремить по кривой АВ к точке М, то положение секущей будет, вообще говоря, изменяться.
Если точку Р устремить по кривой АВ к точке М, то положение секущей будет, вообще говоря, изменяться.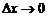 существует предельное положение секущей, то полученная прямая называется касательной к графику
существует предельное положение секущей, то полученная прямая называется касательной к графику 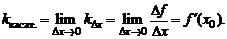
 является угловым коэффициентом касательной.
является угловым коэффициентом касательной. ,
,  , имеющей угловой коэффициент, равный
, имеющей угловой коэффициент, равный  (2)
(2) и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Учитывая условие перпендикулярности двух прямых, запишем уравнение нормали:
и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Учитывая условие перпендикулярности двух прямых, запишем уравнение нормали: (полагаем, что
(полагаем, что  ).
).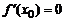 , то нормалью будет прямая
, то нормалью будет прямая 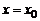 .
.  ,т.е. известно расстояние s (t) от точки М до некоторой начальной точки отсчета в каждый момент времени t. В момент времени
,т.е. известно расстояние s (t) от точки М до некоторой начальной точки отсчета в каждый момент времени t. В момент времени  точка пройдет расстояние
точка пройдет расстояние  , а в момент времени
, а в момент времени  – расстояние
– расстояние  . За промежуток времени
. За промежуток времени  точка М пройдет расстояние
точка М пройдет расстояние 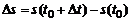 .
. можно рассматривать как среднюю скорость движения на промежутке времени
можно рассматривать как среднюю скорость движения на промежутке времени  . Чем меньше промежуток времени
. Чем меньше промежуток времени  называют скоростью движения (или мгновенной скоростью движения) точки М в момент времени
называют скоростью движения (или мгновенной скоростью движения) точки М в момент времени  , т.е.
, т.е. .
. . Таким образом,
. Таким образом,  , т.е. скорость движения в момент времени
, т.е. скорость движения в момент времени 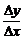 есть средняя скорость изменения зависимой переменной y относительно аргумента x, а
есть средняя скорость изменения зависимой переменной y относительно аргумента x, а  есть скорость изменения y в точке x.
есть скорость изменения y в точке x. и
и  имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что
имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что  ) и справедливы следующие формулы:
) и справедливы следующие формулы: ,
, 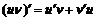 ,
, 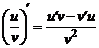 . (1)
. (1) имеет производную в соответствующей точке
имеет производную в соответствующей точке  ,
,  .
.


