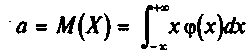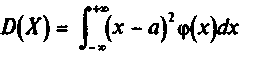1. Дисперсия постоянной величины равна нулю:

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

Это свойство часто используют при вычислении дисперсии. Вычисление по данной формуле дает, например, упрощение расчетов по сравнению с основной формулой, если значения xi случайной величины — целые, а математическое ожидание, а значит и разности (хi-а) — нецелые числа.
4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий:

Обратим внимание на то, что дисперсия как суммы, так и разности независимых случайных величин равна сумме их дисперсий.
Пример. Найти дисперсию случайной величины Z =8X—5Y+7, если известно, что случайные величины Х и Y независимы и D(X) =1,5, D(Y) =1.
Решение. Используя свойства 1, 2, 4 дисперсии, найдем

Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения, называются числовыми характеристиками случайной величины. Обращаем внимание на то, что сама величина X — случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.
№16. Свойства функции распределения и ее плотности.
Общие свойства функции распределения.
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей'.

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
3. На минус бесконечности функция распределения равна нулю, а на плюс бесконечности равна единице, т.е.

4. Вероятность попадания случайной величины в интервал [х1,x2) равна приращению ее функции распределения на этом интервале, т.е.

Пример Функция распределения случайной величины X имеет вид:

Найти вероятность того, что случайная величина примет значение в интервале [1;3).Решение. По формуле

№17. Числовые характеристики непрерывной случайной величины.
Понятие математического ожидания М(Х) и дисперсии D(X), введенные выше для дискретной случайной величины, можно распространить на непрерывные случайные величины.
Для получения соответствующих формул для М(Х) и D(X) достаточно в формулах для дискретной случайной величины Х заменить знак суммирования 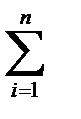 по всем ее значениям знаком интеграла с бесконечными пределами
по всем ее значениям знаком интеграла с бесконечными пределами  , «скачущий» аргумент хi — непрерывно меняющимся х, а вероятность pi — элементом вероятности j(х)dx. Под элементом вероятности понимается вероятность попадания случайной величины X на участок [х, х+dx] (с точностью до бесконечно малых более высоких порядков).
, «скачущий» аргумент хi — непрерывно меняющимся х, а вероятность pi — элементом вероятности j(х)dx. Под элементом вероятности понимается вероятность попадания случайной величины X на участок [х, х+dx] (с точностью до бесконечно малых более высоких порядков).
В результате получим следующие формулы для математического ожидания и дисперсии непрерывной случайной величины X:
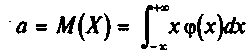
и
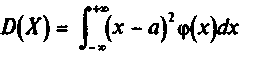
Все свойства математического ожидания и дисперсии, рассмотренные выше для дискретных случайных величин, справедливы и для непрерывных величин.
№18. Функция распределения и плотность распределения вероятностей непрерывной случайной величины.
Задание непрерывной случайной величины с помощью функции распределения не является единственным. Введем понятие плотности вероятности непрерывной случайной величины.
Определение. Плотностью вероятности (плотностью распределения или просто плотностью) j(х) непрерывной случайной величины X называется производная ее функции распределения

Про случайную величину X говорят, что она имеет распределение (распределена) с плотностью j(х) на определенном участке оси абсцисс.
Плотность вероятности j(х), как и функция распределения F(х), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин.
Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения.
График плотности вероятности называется кривой распределения.
Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 3.9).
№19. Начальный и центральный. Асимметрия и эксцесс.
Определение. Начальным моментом k-ro порядка случайной величины X называется математическое ожидание k-й степени этой величины:

Определение. Центральным моментом k-ro порядка случайной величины X называется математическое ожидание k-й степени отклонения случайной величины X от ее математического ожидания:

или

Нетрудно заметить, что при k = 1 первый начальный момент случайной величины X есть ее математическое ожидание, т.е. n1 = М(Х) = а, при k=2 второй центральный момент — дисперсия, т.е. m2 =D(X).
Выше отмечено, что математическое ожидание М(Х), или первый начальный момент, характеризует среднее значение или положение распределения случайной величины X; дисперсия D(X), или второй центральный момент - степень рассеяния распределения X относительно М(Х).
Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент m3 служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на s3, где s — среднее квадратическое отклонение случайной величины X. Полученная величина А называется коэффициентом асимметрии случайной величины:

Если распределение симметрично относительно математического ожидания, то. коэффициент асимметрии А = 0.

Рис.7 Рис.8
На рис. 7 показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию (А>0), а кривая II — отрицательную (левостороннюю) (А < 0).
Четвертый центральный момент m4 служит для характеристики крутости (островершинности или плосковершинности) распределения.,
Эксцессом случайной величины называется число

Число 3 вычитается из отношения потому, что для наиболее часто встречающегося нормального распределения это отношение равно 3. Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные — отрицательным эксцессом (рис. 8).
№20. Законы распределения дискретной случайной величины.













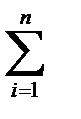 по всем ее значениям знаком интеграла с бесконечными пределами
по всем ее значениям знаком интеграла с бесконечными пределами  , «скачущий» аргумент хi — непрерывно меняющимся х, а вероятность pi — элементом вероятности j(х)dx. Под элементом вероятности понимается вероятность попадания случайной величины X на участок [х, х+dx] (с точностью до бесконечно малых более высоких порядков).
, «скачущий» аргумент хi — непрерывно меняющимся х, а вероятность pi — элементом вероятности j(х)dx. Под элементом вероятности понимается вероятность попадания случайной величины X на участок [х, х+dx] (с точностью до бесконечно малых более высоких порядков).