Методы измерения периода и временных интервалов

Различают два основных метода измерения периода и времен­ных интервалов:

• осциллографический;

• электронно-счетный.

Измерение временных интервалов с помощью осциллографа производится по осциллограмме исследуемого напряжения с ис­пользованием линейной развертки. Из-за значительных погреш­ностей отсчета начала и конца интервала, а также из-за нелиней­ности развертки общая погрешность измерения временных интер­валов составляет единицы процентов. Значительно меньшая по­грешность свойственна специализированным измерителям времен­ных интервалов со спиральной разверткой.

В настоящее время наиболее распространены электронно-счет­ные методы измерения периода и временного интервала. Основными из которых являются:

• цифровой метод измерения интервалов времени;

• метод интерполяции;

• нониусный метод.

Цифровой метод измерения интервалов времени

Принцип измерения периода гармонического сигнала цифровым ме­тодом с помощью цифрового частотомера поясняется рис. 17.1, где приве­дены структурная схема устройства в режиме измерения периода гармо­нического колебания и соответствующие его работе временные диа­граммы.

Измерение интервала времени T_x цифровым методом основано на заполнении его импульсами, следующими с образцовым периодом Т_о, и подсчете числа М_х этих импульсов.

Все элементы устройства и их действие были проанализированы в вопросах, связанных с измерением частоты. Структурный состав генератора опорной частоты при измерении периода рассматривается ниже.

а)

б)

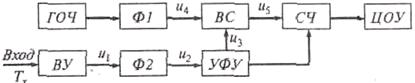
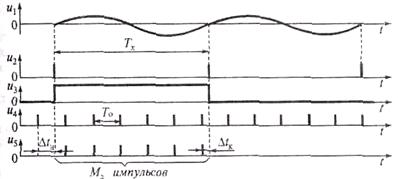
Рис. 3.6. Цифровой метод измерения интервалов времени: а — структурная схема; б — временные диаграммы

 

Гармонический сигнал, период T_x которого требуется измерить, по­сле прохождения входного устройства ВУ (u₁ — выходной сигнал ВУ) и формирователя импульсов Ф2 преобразуется в последовательность ко­ротких импульсов u₂ с аналогичным периодом. В устройстве фор­мирования и управления УФУ из них формируется строб-импульс и_з прямоугольной формы и длительностью T_x, поступающий на один из входов временного селектора ВС. На второй вход этого селектора по­даются короткие импульсы u₄ с образцовым периодом следования Т_о, созданные формирователем Ф1 из колебаний генератора опорной частоты ГОЧ.

Временной селектор ВС пропускает на счетчик СЧ М_х счетных импуль­сов u₄ в течение времени T_x, равном длительности строб-импульса и_з. Измеряемый период T_x, как следует из рис. 17.1, б,

T_x = М_х Т_о + Δt_д,(3.6)

где Δt_д = Δt_к – Δt_н — общая погрешность дискретизации; Δt_н и Δt_к — погрешности дискретизации начала и конца периода Т_х.

Без учета в формуле (17.1) погрешности Δt_д число импульсов, поступившее на счетчик М_х = T_x / Т_о, а измеряемый период пропорционален М_х

T_x = М_х Т_о. (3.7)

Выходной код счетчика СЧ, выдаваемый на цифровое отсчетное уст­ройство ЦОУ, соответствует числу подсчитанных им счетных импульсов М_х, а показания ЦОУ— периоду T_x, поскольку период следования счет­ных импульсов и₅ выбирается из соотношения Т_о = 1^{- n}, где п — целое число. Так, например, при п = 6 ЦОУ отображает число М_х, соот­ветствующее периоду T_x, выраженному в мкс.

Погрешность измерения периода T_x, как и при измерении частоты, имеет систематическую и случайную составляющие.

Систематическая составляющая зависит от стабильности δ_кв образ­цовой частоты ГОЧ (его кварцевого генератора), а случайная опреде­ляется в основном погрешностью дискретизации Δt_д, рассмотренной выше. Максимальное значение этой погрешности удобно учиты­вать через эквивалентное изменение числа счетных импульсов М_х на ±1.

При этом максимальная абсолютная погрешность дискретизации может быть определена разностью двух значений периода T_x, получаемых по формуле (17.2) при М_х ± 1 и М_х и равна Δ T_x = ± Т_о.

Соответствующая мак­симальная относительная погрешность

δ = ± Δ T_x /T_x = ± 1/ М_х = ±1/(T_x f_о),

где f_о = 1/ Т_о — значение образцовой частоты генератора ГОЧ.

На погрешность измерения влияют также шумы в каналах форми­рования строб-импульса и₃ и счетных импульсов и₄ (рис. 17.1, а), вно­сящие в их положение временную модуляцию по случайному закону. Однако в реальных приборах с большим отношением сигнал/шум по­грешность измерения за счет влияния шума пренебрежимо мала по срав­нению с погрешностью дискретизации.

Суммарная относительная погрешность измерения периода опре­деляется в процентах по формуле

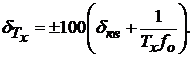(3.8)

Из выражения (17.3) следует, что из-за погрешности дискретизации по­грешность измерения периода T_x резко увеличивается при его уменьшении.

Повышения точности измерений можно добиться за счет увеличения частоты f_о генератора ГОЧ (путем умножения частоты его кварцевого генератора в Ку раз), т.е. за счет увеличения числа счетных импульсов М_х. С этой же целью в схему после входного устройства вводят делитель частоты исследуемого сигнала с коэффициентом деления К (на рис. 17.1, а не показан). При этом выполняется измерение К периодов Т_х и в К раз уменьшается относительная погрешность дискретизации.

Погрешность дискретизации можно уменьшить и способом из­мерений с многократными наблюдениями. Однако при этом зна­чительно увеличивается время измерений. В связи с этим разработаны методы, уменьшающие погрешность дискретизации с существенно меньшим увеличением времени измерения. К их числу относится: метод интерполяции, нониусный метод.

Метод интерполяции

Метод интерполяции состоит в том, что помимо целого числа периодов счетных импульсов, заполняющих измеряемый интервал времени, учитываются и дробные части периода, заключенные между опорным и первым счетным импульсами, а также между последним счетным импульсом и интервальным.

Измерение временных интервалов методом интерполяции поясняет рис. 17.2.

 

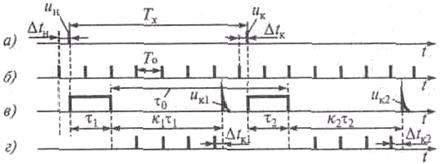
Рис. 3.7. Измерение временного интервала методом интерполяции а — измеряемый интервал, б — счетные импульсы, в — выходные импульсы расширителей, г — группы счетных импульсов отражающих расширенные интервалы

 

Пусть измеряется интервал времени Т_х, начало и конец которого заданы двумя импульсами и_н и и_к, соответственно (рис. 17.2, а). Предпола­гается, что начало измеряемого интервала не связано синхронно со счетными импульсами, приведенными на рис. 17.2, а, б.

Для уменьшения составляющих погрешности дискретизации (Δt_н и Δt_к) в начале и конце интервала Т_х, соответствующие данным погрешно­стям, интервалы расширяют в К раз и каждый измеряют, заполняя счетными импульсами. Учитывая погрешности расширителей, на прак­тике расширяют интервалы большей длительности, например интервалы τ₁ = 2 Т_о - Δt_н и τ₂ = 2 Т_о – Δt_к (рис. 17.2, в). Расширители строят, используя обычно способ заряда и разряда конденсатора с разной скоростью.

На рис. 17.2, в приведены выходные импульсы расширителей и_к1 и и_к2, определяющие конец расширенных интервалов, а собственно расширен­ные интервалы обозначены через к₁τ₁ и к₂τ₂.

Расширенные интервалы, а также интервал τ_о между концами им­пульсов τ₁ и τ₂ измеряют цифровым методом, используя каналы, содер­жащие временной селектор и счетчик. Счетные импульсы, поступившие на вход каждого счетчика при измерении расширенных интервалов, по­казаны на рис. 17.2, г. Измеряемые интервалы, как следует из рис. 17.2, можно представить в виде

к₁τ₁ = N₁Т_о+ Δt_к1; к₂τ₂ = N₂Т_о+ Δt_к2; τ_о = N_oТ_о, (3.9)

где к₁ и к₂ — коэффициенты расширения; N_o, N₁ и N₂ — числа счетных импульсов, заполнивших отмеченные интервалы, а Δt_к1 и Δt_к2 — по­грешности дискретизации измерения расширенных интервалов.

Из рис. 17.2 также видно, что искомый интервал

Т_х = τ_о + τ₁ - τ₂.

Под­ставляя в это выражение параметры τ_о, τ₁ и τ₂, вычисляемые по (17.4), находим, что

Т_х = N_oТ_о + (N₁Т_о+ Δt_к1)/ к₁ – (N₂Т_о+ Δt_к2)/ к₂. (17.5)

При идентичности коэффициентов расширения (к₁ = к₂ = к), получим

Т_х = Т_о [ N_o +(N₁ – N₂)/ к +(Δt_к1 – Δt_к2)/ к ]. (3.10)

Погрешности дискретизации Δt_к1 и Δt_к2 имеют равномерное распре­деление с пределами 0… Т_о, а их разность Δt_к1 – Δt_к2 распределена по тре­угольному закону с пределами ± Т_о. Поэтому максимальная погрешность дискретизации при измерении интервала Т_х равна Т_о / к и уменьшается по мере роста коэффициента расширения k. Однако на практике данный коэф­фициент выбирают равным 128 или 256, так как при его дальнейшем уве­личении существенно возрастает погрешность расширителей интервалов.

Нониусный метод

Одной из разновидностей метода интерполяции является нониусный метод, часто используемый в технике измерения линей­ных размеров. Нониусные измерители временных интервалов в прин­ципе позволяют уменьшить погрешности начала и конца счета. Однако в большинстве приборов счетные импульсы синхронизиро­ваны с началом временного интервала и уменьшается лишь погреш­ность конца.

Структурная схема измерителя временного интервала с нониусным счетом показана на рис. 17.3, а.

Импульс и_н начала времен­ного интервала запускает генератор счетных импульсов с удар­ным возбуждением и воздействует на триггер 1. Выходной импульс триггера отпирает селектор 1 и начинается счет импульсов с пе­риодом Т_о. Под действием импульса и_к конца интервала триггер 1 переходит в исходное положение и счет прекращается. Счетчик фик­сирует число N, кратное целому числу периодов счетных импуль­сов. В момент окончания временного интервала происходит запуск генератора нониусных импульсов, одновременно импульсом с триггера 2 открывается селектор 2. Нониусные импульсы с периодом

Т_н = (п — 1)Т_о/п,

где п — некоторое целое число, поступают на счетчик нониусных импульсов и на схему совпадений.

 

 

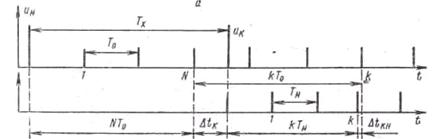
Рис. 3.7. Нониусный метод измерения временных интервалов: а – структурная схема; б – временные диаграммы

 

С течением времени интервал между соседними импульсами счетной и нониусной последовательностей уменьшается, и при его минимальном зна­чении импульсы начинают перекрываться. Срабатывает схема сов­падений, импульс которой воздействует на селектор 2 и приводит к прекращению счета по нониусному каналу. Счетчик нониусных импульсов фиксирует число нониусных импульсов k.

Как видно из рис. 17.3, б, измеряемый временной интервал можно представить в виде суммы

Т_х = NТ_о + Δt_к, (3.11)

где

Δt_к = kТ_о – kТ_н – Δt_кн = kТ_о /п – Δt_кн, (3.12)

Δt_кн — погрешность из-за неточного совпадения фронтов счетных и нониусных импульсов.

Подставив (17.8) в (17.7), получим

Т_х = NТ_о + kТ_о /п – Δt_кн, (3.13)

Число k характеризует длительность интервала Δt_к, выраженную в долях периода Т_о. Величина Т_о /п называется шагом нониуса.

Отсчетное устройство прибора связано с обоими счетчиками та­ким образом, что число N фиксируется в его старших разрядах, а k — в младших. Обычно п = 10^m, где m == 1 или 2, тогда с младших разрядов отсчетного устройства отсчитывается значение Δt_к в де­сятых или сотых долях Т_о.

Пусть, например Т_о = 100 нc, Т_н = 99 нc, a Т_х = 1813 нc. Отсчет старших разрядов отсчетного устройства будет равным 18, а интервал Δt_к составит 13 не. Совпа­дение импульсов произойдет при выполнении равенства 13 = k 100 – k 99 откуда отсчет младших разрядов k == 13. Общий отсчет равен 1813, что соответствует длительности измеряемого интервала в наносекундах.

Нониусные и счетные импульсы обычно формируются из сину­соидальных напряжений, вырабатываемых генераторами с кварце­вой стабилизацией. Из-за нестабильности уровней формирования периоды счетных и нониусных импульсов флуктуируют вокруг сред­них значений Т_о и Т_н. При большом числе п это может привести к ложным совпадениям. Такое же влияние оказывает нестабиль­ность начальной фазы генератора нониусных импульсов. Перечис­ленные факторы ограничивают точность измерений.

 

Вопрос №3

3.1