Лекция №7
Тема: Измерение частоты, интервалов времени и фазового сдвига
Цель:
Рассмотреть методы измерения частоты, интервалов времени и разности фаз сигналов
Вопросы:
1. Измерение частоты.
2. Измерение интервалов времени.
3. Измерение фазового сдвига.
Литература по дисциплине:
Основная: 1. Метрология и радиоизмерения: Учебник для вузов./.И. Нефедов, В.И. Хахин, В.К. Битюков и др./ Под ред. проф. Нефедова. – М.: Высш. шк., 2006. – 526с.
Литература по теме лекции: [1], с. 273-289
Вопрос №1
Общие сведения
Напряжение гармонического колебания, как известно, имеет вид:
u = UcosФ = Ucos(ωt + φ0), (3.1)
где U — амплитуда, Ф — фаза колебания, ω = 2π — круговая частота и φ0 — начальная фаза колебания.
Частота в момент времени t является производной фазы по времени

и называется мгновенной частотой.
Измерение выполняется в течение некоторого интервала времени τи, на протяжении которого измеряемая частота усредняется. Следовательно, значение частоты, полученное в результате измерения, всегда является усредненной величиной.
Частотой колебаний называется число колебаний в единицу времени:
f = n/t,
где t — интервал времени существования n колебаний.
Единица частоты «герц» (Гц) определяется как одно колебание в одну секунду. Частота и время неразрывно связаны между собой, поэтому измерение величины одной из них можно заменять измерением другой.
В Международной системе единиц СИ время принято за одну из шести основных физических величин. Секунда – 9 192 631 770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Частота электромагнитных колебаний связана с периодом колебания и длиной однородной плоской волны в свободном пространстве следующими соотношениями:
 , fT = 1 и fλ = с,
, fT = 1 и fλ = с,
где с — скорость света.
Скорость света в свободном пространстве с = 3 105 км/с, однако в воздухе по данным измерений на многих частотах скорость распространения электромагнитных колебаний меньше. Рекомендуется принимать значение свозд = 299 792,5 ± 0,3 км/с.
Спектр частот электрических колебаний, используемых в радиотехнике, простирается от долей герца до тысяч гигагерц. Этот спектр разделяют на два диапазона — низких и высоких частот.
К низким частотам относят инфразвуковые (ниже 20 Гц) и звуковые (от 20 до 20000 Гц). Высокочастотный диапазон, в свою очередь, разделяют на высокие частоты (от 20 кГц до 30 МГц), ультравысокие (от 30 до 300 МГц) и сверхвысокие (выше 300 МГц).
Такое разделение объясняется различными физическими свойствами электрических колебаний в указанных участках спектра, разными способами их получения и особенностями передачи на расстояние. Однако четкой границы между отдельными участками спектра провести невозможно, поэтому такое деление является условным.
Международный консультативный комитет по радио (МККР) в 1959 г. принял решение об упорядочении наименований в спектре частот, применяемом для радиосвязи, радиовещания и телевидения. Этот спектр разбит на девять полос, которые обозначаются цифрами от 4 до 12, качественными и метрическими наименованиями частот и длин волн и соответствующими буквенными сокращениями.
В радиотехнической практике чаще всего измеряется частота, иногда период колебания и реже длина волны. Измерение частоты и времени выполняется с наибольшей точностью по сравнению с другими видами радиоизмерений, поэтому многие физические величины, подлежащие измерению, преобразуются во временные или частотные функции для последующего точного измерения.
Погрешность измерения частоты задается в абсолютных (Δf = fx - fоб) или, чаще, в относительных (δ = Δf/fоб) величинах, где fоб — значение образцовой частоты.
Методы измерения частоты
В зависимости от участка спектра применяют различные методы измерения.
Наиболее распространенными являются:
• метод перезаряда конденсатора,
• методы сравнения:
• осциллографический,
• резонансный метод,
• гетеродинный метод,
• метод дискретного счета.
На основе методов перезаряда конденсатора и дискретного счета созданы прямопоказывающие приборы частотомеры. Метод сравнения являются трудоемкими, требуют обработки полученных данных и используются в основном для градуировки генераторов различных измерительных приборов. Для их реализации необходим образцовый генератор более высокой точности и устройство сравнения (сличения) частот.
Допустимая погрешность определяется применяемым методом и заключается в пределах:
от 1 до 2 % при измерении методом перезаряда конденсатора;
от 10-4 до 10-8 — при измерении методами сравнения;
10-8 и меньше — при измерении методом дискретного счета.
Рассмотрим более подробно перечисленные выше методы.
Вопрос №2
Общие сведения
Раздел метрологии, занимающийся изучением методов и средств измерения времени и интервалов времени, называют хронометрией.
Свойства времени как объекта измерений определяются его физической сущностью. Главными из них являются:
• одномерность,
• однонаправленность,
• бесконечность,
• цикличность.
Одномерность времени означает, что моменты времени следуют вдоль одной координаты. Это позволяет характеризовать время одним числом.
Однонаправленность времени подчеркивает упорядоченный характер временного развития, его необратимость, когда причина не может опережать следствие и никаким образом нельзя возвратиться в прошлое. Одномерность и однонаправленность времени позволяют при измерении пользоваться одним
Бесконечность времени определяется свойствами материи, находящейся в непрерывном изменении и развитии. Время никогда не начиналось и никогда не кончится. То, что мы отсчитываем даты от какого-либо исторического события, отражает лишь условность шкалы времени, а не ее начало.
Цикличность времени отражает периодичность процессов, происходящих в природе, когда мы наблюдаем смену времен года, суток, периодичность процессов, происходящих в живых организмах.
Единица времени является одной из семи основных единиц Международной системы СИ. Способы измерения времени постоянно развиваются, так как этого требовали в первую очередь астрономия, навигация и геодезия. В настоящее время достигнута относительная погрешность измерения времени 10-15. Таким образом, время представляет собой основную физическую величину, которая может быть измерена с наивысшей точностью.
В промышленности требуемая точность измерения времени редко превышает 10-6 (примерно 0,1 с/сут). Однако в связи с необходимостью измерения других физических величин, например в радио- и оптической локации космических объектов, в радионавигации, в аналого-цифровых преобразователях напряжений, работающих по принципу двойного интегрирования, возникает потребность использования еще больших точностей измерения времени. Среди ряда технических задач можно назвать такие, в которых измерение интервалов времени и непосредственно связанное с этим определение частоты определяют основные характеристики и принципы построения аппаратуры для исследования различных процессов в устройствах вычислительной техники, связи, телевидения, электроники, ядерной физики, медицины и др.
Основной единицей времени во всех системах единиц является секунда (с). Ее определение изменялось в соответствии с потребностями науки и техники приборостроения. До 1956 г. в качестве единицы времени была принята 1/89400 средних солнечных суток. С 1967 г. размер единицы времени равен секундеСИ, которая определяется как интервал времени, в течение которого совершается 9192631770 периодов излучения, соответствующих переходу между двумя уровнями структуры основного состояния атома цезия-133 при отсутствии возмущения внешними полями.
Интервалом времени Δt в общем случае называется время, прошедшее между моментами двух последовательных событий. К числу таких интервалов относятся, например, период колебаний, длительность импульса или длительность интервала, определяемая разносом по времени двух импульсов.
Периодом Т любого периодического детерминированного сигнала u(t) называется наименьший интервал времени, через который регулярно и последовательно повторяется произвольно выбранное мгновенное значение этого сигнала. Отсюда следует, что u(t) = u(t + пТ), где п = 1, 2, 3 и т.д. Для гармонического сигнала, например для u(t) = Umsin(2nt/T) = Umsin(φ(t)), период колебания Т можно также определить, как интервал времени, в течение которого фаза сигнала φ(t), выраженная в радианах, изменяется на 2π.
Метод интерполяции
Метод интерполяции состоит в том, что помимо целого числа периодов счетных импульсов, заполняющих измеряемый интервал времени, учитываются и дробные части периода, заключенные между опорным и первым счетным импульсами, а также между последним счетным импульсом и интервальным.
Измерение временных интервалов методом интерполяции поясняет рис. 17.2.
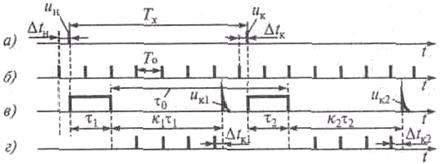
Рис. 3.7. Измерение временного интервала методом интерполяции а — измеряемый интервал, б — счетные импульсы, в — выходные импульсы расширителей, г — группы счетных импульсов отражающих расширенные интервалы
Пусть измеряется интервал времени Тх, начало и конец которого заданы двумя импульсами ин и ик, соответственно (рис. 17.2, а). Предполагается, что начало измеряемого интервала не связано синхронно со счетными импульсами, приведенными на рис. 17.2, а, б.
Для уменьшения составляющих погрешности дискретизации (Δtн и Δtк) в начале и конце интервала Тх, соответствующие данным погрешностям, интервалы расширяют в К раз и каждый измеряют, заполняя счетными импульсами. Учитывая погрешности расширителей, на практике расширяют интервалы большей длительности, например интервалы τ1 = 2 То - Δtн и τ2 = 2 То – Δtк (рис. 17.2, в). Расширители строят, используя обычно способ заряда и разряда конденсатора с разной скоростью.
На рис. 17.2, в приведены выходные импульсы расширителей ик1 и ик2, определяющие конец расширенных интервалов, а собственно расширенные интервалы обозначены через к1τ1 и к2τ2.
Расширенные интервалы, а также интервал τо между концами импульсов τ1 и τ2 измеряют цифровым методом, используя каналы, содержащие временной селектор и счетчик. Счетные импульсы, поступившие на вход каждого счетчика при измерении расширенных интервалов, показаны на рис. 17.2, г. Измеряемые интервалы, как следует из рис. 17.2, можно представить в виде
к1τ1 = N1То+ Δtк1; к2τ2 = N2То+ Δtк2; τо = NoТо, (3.9)
где к1 и к2 — коэффициенты расширения; No, N1 и N2 — числа счетных импульсов, заполнивших отмеченные интервалы, а Δtк1 и Δtк2 — погрешности дискретизации измерения расширенных интервалов.
Из рис. 17.2 также видно, что искомый интервал
Тх = τо + τ1 - τ2.
Подставляя в это выражение параметры τо, τ1 и τ2, вычисляемые по (17.4), находим, что
Тх = NoТо + (N1То+ Δtк1)/ к1 – (N2То+ Δtк2)/ к2. (17.5)
При идентичности коэффициентов расширения (к1 = к2 = к), получим
Тх = То [ No +(N1 – N2)/ к +(Δtк1 – Δtк2)/ к ]. (3.10)
Погрешности дискретизации Δtк1 и Δtк2 имеют равномерное распределение с пределами 0… То, а их разность Δtк1 – Δtк2 распределена по треугольному закону с пределами ± То. Поэтому максимальная погрешность дискретизации при измерении интервала Тх равна То / к и уменьшается по мере роста коэффициента расширения k. Однако на практике данный коэффициент выбирают равным 128 или 256, так как при его дальнейшем увеличении существенно возрастает погрешность расширителей интервалов.
Нониусный метод
Одной из разновидностей метода интерполяции является нониусный метод, часто используемый в технике измерения линейных размеров. Нониусные измерители временных интервалов в принципе позволяют уменьшить погрешности начала и конца счета. Однако в большинстве приборов счетные импульсы синхронизированы с началом временного интервала и уменьшается лишь погрешность конца.
Структурная схема измерителя временного интервала с нониусным счетом показана на рис. 17.3, а.
Импульс ин начала временного интервала запускает генератор счетных импульсов с ударным возбуждением и воздействует на триггер 1. Выходной импульс триггера отпирает селектор 1 и начинается счет импульсов с периодом То. Под действием импульса ик конца интервала триггер 1 переходит в исходное положение и счет прекращается. Счетчик фиксирует число N, кратное целому числу периодов счетных импульсов. В момент окончания временного интервала происходит запуск генератора нониусных импульсов, одновременно импульсом с триггера 2 открывается селектор 2. Нониусные импульсы с периодом
Тн = (п — 1)То/п,
где п — некоторое целое число, поступают на счетчик нониусных импульсов и на схему совпадений.

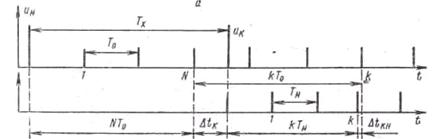
Рис. 3.7. Нониусный метод измерения временных интервалов: а – структурная схема; б – временные диаграммы
С течением времени интервал между соседними импульсами счетной и нониусной последовательностей уменьшается, и при его минимальном значении импульсы начинают перекрываться. Срабатывает схема совпадений, импульс которой воздействует на селектор 2 и приводит к прекращению счета по нониусному каналу. Счетчик нониусных импульсов фиксирует число нониусных импульсов k.
Как видно из рис. 17.3, б, измеряемый временной интервал можно представить в виде суммы
Тх = NТо + Δtк, (3.11)
где
Δtк = kТо – kТн – Δtкн = kТо /п – Δtкн, (3.12)
Δtкн — погрешность из-за неточного совпадения фронтов счетных и нониусных импульсов.
Подставив (17.8) в (17.7), получим
Тх = NТо + kТо /п – Δtкн, (3.13)
Число k характеризует длительность интервала Δtк, выраженную в долях периода То. Величина То /п называется шагом нониуса.
Отсчетное устройство прибора связано с обоими счетчиками таким образом, что число N фиксируется в его старших разрядах, а k — в младших. Обычно п = 10m, где m == 1 или 2, тогда с младших разрядов отсчетного устройства отсчитывается значение Δtк в десятых или сотых долях То.
Пусть, например То = 100 нc, Тн = 99 нc, a Тх = 1813 нc. Отсчет старших разрядов отсчетного устройства будет равным 18, а интервал Δtк составит 13 не. Совпадение импульсов произойдет при выполнении равенства 13 = k 100 – k 99 откуда отсчет младших разрядов k == 13. Общий отсчет равен 1813, что соответствует длительности измеряемого интервала в наносекундах.
Нониусные и счетные импульсы обычно формируются из синусоидальных напряжений, вырабатываемых генераторами с кварцевой стабилизацией. Из-за нестабильности уровней формирования периоды счетных и нониусных импульсов флуктуируют вокруг средних значений То и Тн. При большом числе п это может привести к ложным совпадениям. Такое же влияние оказывает нестабильность начальной фазы генератора нониусных импульсов. Перечисленные факторы ограничивают точность измерений.
Вопрос №3
3.1
3.2
Методы измерения фазового сдвига
К основным методам измерения фазового сдвига относятся:
- осциллографический,
- компенсационный,
- преобразования фазового сдвига в импульсы тока,
- дискретного или цифрового счета,
- с преобразованием частоты.
Осциллографический метод
Для измерения фазового сдвига с помощью осциллографа применяются следующие методы:
- линейной развертки,
- синусоидальной развертки,
- круговой развертки,
- метод полуокружности.
Метод линейной развертки реализуется при наблюдении на экране одновременно двух сигналов (см. рис. 12.1). Для этого можно использовать двухлучевой осциллограф, подавая сигналы на входы вертикального отклонения лучей (входы Y). Можно также применить однолучевой осциллограф, если на его вход Y подавать исследуемые сигналы поочередно через электронный коммутатор. В том и другом вариантах горизонтальные развертки осциллографов должны быть синхронизированы одним из сигналов. Измерив временные отрезки Dt и Т, вычисляют фазовый сдвиг сигналов в радианах по формуле (12.2) или в градусах по следующему выражению:
Dj = 360 ° Dt/T. (3.16)
При данном методе погрешность измерения фазового сдвига Dj близка к ±(5...7)° и вызвана нелинейностью развертки, неточностью замера интервалов Dt и Т, а также ошибками определения положения оси времени.
Метод синусоидальной развертки или эллипса
Реализуется с помощью однолучевого осциллографа при подаче одного сигнала на вход Y, а второго — на вход X отклонения луча. При этом генератор развертки осциллографа должен быть выключен.
Пусть на входы X и Y были поданы соответственно сигналы u1(t) = u1= Um1sin(wt) и u2(t) = u2 = Um2sin(wt +j), для которых фазовый сдвиг Dj = j (далее в выражениях для u1(t) и u2(t) аргумент t везде опущен). Мгновенные отклонения луча на экране по горизонтали и вертикали равны:
х = hxUm1sinwt = asinwt,(3.17)
y = hyUy2sin(wt +j) = b sin(wt +j), (3.18)
где коэффициенты hx, hy — чувствительности осциллографа к отклонению луча по горизонтали и вертикали; а = hxUm1, b = hyUy2 — амплитуды отклонения луча.
Для определения формы фигуры, вычерчиваемой лучом на экране осциллографа, найдем ее аналитическую запись. Для этого достаточно исключить из формул (12.4) и (12.5) переменную t и затем представить отклонение у в зависимости от величины х:
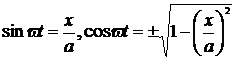 , (3.19)
, (3.19)
y = b sin(wt +j) = b (sinwt cosj +coswt sinj), (3.20)
После подстановки (12.6) в (12.7) получим выражение
 , (3.21)
, (3.21)
представляющее собой известное уравнение эллипса (рис. 12.2).

Рис. 3.7. К измерению разности фаз методом эллипса
Определим величину фазового сдвига двух сегментов. Частям эллипса, представленным непрерывной и штриховой линиями (рис. 12.2), соответствует уравнение (12.8), в котором перед корнем стоят знаки плюс и минус соответственно. Величины отрезков у0 и х0 находятся по уравнению (12.8), если положить для непрерывной линии х = 0, а для штриховой у = 0:
у0 = bsinw,х0 = asinw.
Отсюда искомый фазовый сдвиг:
 , (3.22)
, (3.22)
Перед началом измерения Dj обычно уравнивают на экране амплитуды b и а (рис. 12.2). Для этого поочередно отключают сигналы u1 и u2 от входов X и Y и с помощью регулировок чувствительности hx или hy добиваются равенства b = а, когда у0 = х0. Измерив на экране отрезки 2 у0 и 2 b (или 2 х0 и 2 а), подставляют их отношение в формулу (12.9) и вычисляют Dj.
Метод эллипса не позволяет однозначно определить фазовый сдвиг в диапазоне (0...360)0. Это наглядно видно из осциллограмм, представленных на рис. 12.3, соответствующих различным значениям Dj.
Добиться достаточно точного результата измерений сдвига фаз можно, подав один из сигналов на осциллограф через фазовращатель на 90° и проследив за изменением вида осциллограммы. Положим, что имели осциллограмму, соответствующую сдвигу фаз Dj = 60° или 300°. Если теперь подадим сигнал u2 на вход Y через фазовращатель, то фазовый сдвиг станет равен 150° или 30°. Как видно из рис. 12.3, при Dj = 60° осциллограмма из 1-го и 3-го квадрантов переместится в 3-й и 4-й, а при Dj = 300° останется в 1-м и 3-м квадрантах.
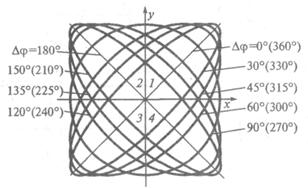
Рис. 3.8. Метод эллипса: осциллограммы при разных фазовых сдвигах
Погрешность измерения фазового сдвига между двумя синусоидальными сигналами методом эллипса зависит от точности измерения длин отрезков, входящих в выражение (12.9), и точности фокусировки луча на экране осциллографа. Эти причины оказывают тем большее влияние, чем ближе измеряемый сдвиг фаз к нулю или к 90°. Возможна также систематическая погрешность измерения из-за наличия различного фазового сдвига, создаваемого усилителями каналов вертикального и горизонтального отклонения лучей. Для ее устранения можно (перед началом измерений) подать один из исследуемых сигналов на вход Y осциллографа непосредственно, а на вход X — через регулируемый фазовращатель. Изменяя настройку фазовращателя, необходимо добиться появления на экране осциллографа наклонной прямой линии. Затем, сохраняя эту настройку, подать на вход фазовращателя второй сигнал (отключив предварительно первый) и провести требуемое измерение фазового сдвига сигналов.
Метод круговой развертки
Обеспечивает измерение фазового сдвига практически в пределах от 0 до 360°. Сущность метода поясняется схемами и эпюрами, приведенными на рис. 12.4, для случая измерения фазового сдвига между сигналами u1= Um1sinwt и u2 = Um2sinw(Dt-t).
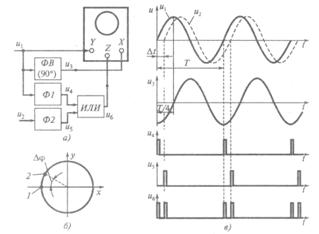
Рис. 3.9. Метод круговой развертки: а — схема измерения; б — осциллограмма;
в — эпюры сигналов
Генератор развертки осциллографа предварительно выключается и на входы Y и X подаются сигнал u1 и сигнал u3 (рис. 12.4, а), задержанный относительно u1 по фазе на 90° (с помощью дополнительного фазовращателя ФВ). При одинаковом отклонении электронного луча по горизонтали и вертикали на экране осциллографа будет наблюдаться осциллограмма, имеющая вид окружности (рис. 12.4, б).
Анализируемые сигналы u1 и u2 также поступают на входы идентичных формирователей Ф1 и Ф2, преобразующих синусоидальные колебания в последовательность коротких однополярных импульсов u4 и u5 (рис. 12.4, в). Передние фронты этих импульсов практически совпадают с моментом перехода синусоид через нулевое значение при их возрастании. Импульсные сигналы u4 и u5 объединяются с помощью логической схемы ИЛИ. Ее выходной импульсный сигнал u6 в виде двухимпульсных последовательностей подается на вход Z управления яркостью луча осциллографа. В результате на окружности (рис. 12.4, б) в точках 1 и 2 появляются отметки повышенной яркости.
Измерение фазового сдвига Dj между сигналами u1 и u2 выполняется так, как показано на рис. 12.4, б. Для измерения используется прозрачный транспортир, центр которого совмещается с центром окружности. Данный метод измерения основан на следующем. Полную окружность, которой соответствует угол 360°, луч описывает за время, равное периоду Т сигналов u1 и u2 , а дугу между точками 1 и 2, которой соответствует некоторый угол a, — за время задержки этих сигналов Dt = DjT / 3600. Отсюда следует, что угол a равен Dj.
На погрешность измерения влияют точности формирования окружности и определения ее центра, а также степень идентичности порога срабатывания формирователей и точность измерения угла Dj с помощью транспортира.
Компенсационный метод
Компенсационный метод основан на сравнении измеряемого фазового сдвига с известной величиной фазового сдвига, которую создает измерительный фазовращатель.
Структурная схема измерительной установки приведена на рис. 12.5. Она содержит измерительный фазовращатель ФВ и индикатор равенства фаз, в качестве которого использован осциллограф с отключенным генератором развертки. Сигнал u1 подается на вход Y осциллографа через ФВ, а сигнал u2 на вход X — непосредственно.
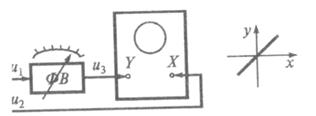
Рис. 3.10. К определению фазового сдвига компенсационным методом
Фазовый сдвиг Dj между двумя сигналами u1 и u2 определяется путем изменения фазы дополнительного сигнала из с помощью ФВ до момента появления на экране наклонной прямой линии (см. рис. 12.5), т.е. до момента равенства фаз сигналов u2 и u3. При этом искомый фазовый сдвиг Dj считывается по шкале ФВ. Для более точных измерений следует проверить и скомпенсировать возможное неравенство фазовых сдвигов, даваемых усилителями вертикального и горизонтального отклонения луча осциллографа. Это выполняется в порядке, изложенном выше, при рассмотрении метода эллипса.
Точность измерения компенсационным методом высокая. Погрешность измерения определяется в основном качеством градуировки шкалы фазовращателя и достигает (0,1...0,2)°.
3.3
Суть методов преобразования фазового сдвига в импульсы тока и дискретного или цифрового счета рассмотрим на примере реализации данных методов в средствах измерения разности фаз, которые согласно ГОСТ 15098-86 относятся к подгруппе Ф (Приборы для измерения разности фаз и группового времени запаздывания) и делятся на следующие виды:
Ф1 Установки или приборы для поверки измерителей разности фаз и группового времени запаздывания;
Ф2 Измерители разности фаз (приборы для измерения разности фаз между двумя сигналами одной частоты);
Ф4 Измерители группового времени запаздывания (приборы для измерения крутизны фазочастотных характеристик радиоустройств);
Ф5 Измерители разности фаз импульсные (приборы для измерения разности фаз между двумя импульсно-модулированными сигналами одной частоты).
Фазометр преобразования фазового сдвига в импульсы тока
Структурная схема устройства, реализующего метод преобразование фазового сдвига в импульсы тока, и поясняющие его эпюры, приведены на рис. 12.6.
В состав устройства входят преобразователь Dj ® Dt искомого фазового сдвига Dj в интервал времени Dt и измерительный прибор. Преобразователь имеет два одинаковых формирователя Ф1 и Ф2 и триггер Т.
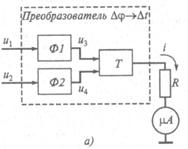

Рис. 3.11. Метод преобразования фазового сдвига в импульсы тока: а — схема устройства; б — эпюры сигналов
Синусоидальные сигналы u1 и u2 , имеющие некоторый фазовый сдвиг Dj, подаются на идентичные формирователи Ф1 и Ф2, преобразующие их в последовательности коротких импульсов u3 и u4 (рис. 12.6, б). Импульсы u3 запускают, а импульсы u4 сбрасывают триггер Т в исходное состояние. В результате на выходе триггера формируется периодическая последовательность импульсов напряжения, период повторения и длительность которых равны периоду Т и сдвигу во времени Dt исследуемых сигналов u1 и u3. Данные импульсы, поступая на резистор R, соединенный с измерительным прибором mА, преобразуются в последовательность импульсов тока i с аналогичными периодом и длительностью и некоторой амплитудой Im (рис. 12.6, б).
В качестве измерительного прибора часто используется микроамперметр магнитоэлектрической системы, реагирующий на среднее значение тока i за период его следования Т. Пусть SI и icp, — чувствительность прибора и среднее значение протекающего через него тока. Тогда показание прибора а определится по несложной формуле
 . (3.23)
. (3.23)
С учетом выражения (12.3) получим
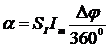 , (3.24)
, (3.24)
где Dj — искомый фазовый сдвиг.
Так как чувствительность SI, и амплитуда Im постоянны, то шкалу микроамперметра можно проградуировать непосредственно в градусах. Измеренное значение фазового сдвига является средним за время измерения.
Рассмотренное устройство является прямопоказывающим фазометром с равномерной шкалой. Диапазон его рабочих частот ограничен снизу инерционностью магнитоэлектрического прибора, а сверху — неидеальностью фронтов импульсов формирователей Ф1 и Ф2, влияющих на четкость работы триггера Т.
В качестве примера отметим параметры одного из фазометров, в основе работы которого используется изложенный метод. Диапазон рабочих частот фазометра от 20 Гц до 1 МГц; измеряемая разность фаз составляет ±180°, т.е. фазовый сдвиг измеряется в диапазоне (0...180)0. Погрешность измерений на частотах до 200 кГц равна (0,5±0,15 Dj)°, а на частотах до 1 МГц — (1 ±0,02 Dj)°.
Цифровой фазометр
Метод дискретного счета (более точное название — цифровой метод измерения фазового сдвига), используемый в цифровых фазометрах, включает две основные операции:
- преобразование фазового сдвига в соответствующий интервал времени;
- измерение интервала времени методом дискретного счета.
Рассмотрим реализацию метода дискретного счета в простейшем цифровом фазометре (рис. 12.7, а), в состав которого входят преобразователь Dj ® Dt искомого фазового сдвига Dj в интервал времени Dt, временной селектор ВС1, генератор счетных импульсов ГИ, счетчик СЧ и цифровое отсчетное устройство ЦОУ.
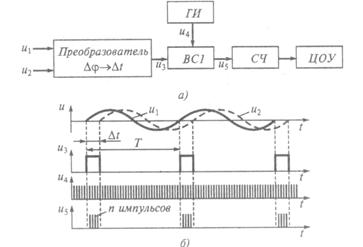
Рис. 3.12 Цифровой метод измерения фазового сдвига.
а — структурная схема; б — временные диаграммы
Устройство и принцип действия преобразователя Dj ® Dt рассмотрены выше. Временной селектор представляет собой ключевую логическую схему. Генератор счетных импульсов состоит из кварцевого генератора гармонических колебаний стабильной частоты и схемы формирования импульсов.
Цифровой фазометр работает следующим образом. Преобразователь Dj ® Dt из подаваемых на его входы синусоидальных сигналов u1 и u2, имеющих фазовый сдвиг Dj, формирует последовательность прямоугольных импульсов u3 (рис. 12.7, б), имеющих длительность Dt и период повторения Т, равные соответственно сдвигу во времени и периоду сигналов u1 и u2.
Импульсы u3, а также счетные импульсы u4 вырабатываемые генератором ГИ, подаются на входы временного селектора ВС1. Данный селектор открывается на время, равное длительности Dt импульсов u3, и в течение этого времени пропускает на выход импульсы генератора u4. При этом на выходе селектора ВС1 формируются пакеты импульсов u5, следующие с периодом Т.
За один период повторения Т сигналов u1 и u2 на счетчик СЧ с выхода селектора поступает количество импульсов, содержащееся в одном пакете и равное
n =Dt/T0, (3.25)
где T0 — период следования счетных импульсов генератора ГИ.
Подставляя в (12.12) соотношение для Dt, из (12.3) находим выражение для измеряемого фазового сдвига сигналов u1 и u2:
Dj = n 3600 T0 / T. (3.26)
Кодовый сигнал со счетчика, пропорциональный фазовому сдвигу Dj, подается на цифровое отсчетное устройство, показания которого выдаются в градусах.
Погрешность данного цифрового фазометра определяется погрешностью дискретности и аппаратурной погрешностью. Погрешность дискретности связана с тем, что интервал времени Dt можно измерить с точностью до одного периода счетных импульсов. Аппаратурная погрешность определяется нестабильностью времени срабатывания триггера преобразователя Dj ® Dt.
Для уменьшения погрешностей используют фазометры среднего значения, результат измерения которых является средним значением измеряемого фазового сдвига за большое число периодов Т.
| | Профессор кафедры
А. Елисеев
|
Лекция №7
Тема: Измерение частоты, интервалов времени и фазового сдвига
Цель:
Рассмотреть методы измерения частоты, интервалов времени и разности фаз сигналов
Вопросы:
1. Измерение частоты.
2. Измерение интервалов времени.
3. Измерение фазового сдвига.
Литература по дисциплине:
Основная: 1. Метрология и радиоизмерения: Учебник для вузов./.И. Нефедов, В.И. Хахин, В.К. Битюков и др./ Под ред. проф. Нефедова. – М.: Высш. шк., 2006. – 526с.
Литература по теме лекции: [1], с. 273-289
Вопрос №1
Общие сведения
Напряжение гармонического колебания, как известно, имеет вид:
u = UcosФ = Ucos(ωt + φ0), (3.1)
где U — амплитуда, Ф — фаза колебания, ω = 2π — круговая частота и φ0 — начальная фаза колебания.
Частота в момент времени t является производной фазы по времени

|
|
|






 , fT = 1 и fλ = с,
, fT = 1 и fλ = с,


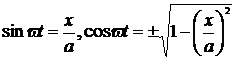 , (3.19)
, (3.19) , (3.21)
, (3.21)
 , (3.22)
, (3.22)




 . (3.23)
. (3.23)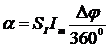 , (3.24)
, (3.24)



