Начнем с точечных оценок и рассмотрим оценку произвольного параметра (среднего, дисперсии или какого-то другого) генеральной совокупности, который обозначим a. Оценивая параметр a по выборке, находим такую величину  , которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований:
, которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований:
1. Состоятельность. Точечная оценка  называется состоятельной, если при неограниченном увеличении объема выборки (
называется состоятельной, если при неограниченном увеличении объема выборки ( ) она стремится к истинному значению параметра a.
) она стремится к истинному значению параметра a.
В математической статистике показывается, что состоятельной оценкой генерального среднего значения, является выборочное среднее арифметическое, а состоятельной оценкой генеральной дисперсии — выборочная дисперсия. 2.Несмещенность. Оценка  называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра a.
называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра a.
Выборочное среднее арифметическое является несмещенной оценкой генерального среднего.
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия, вычисляемая по формуле:
для несгруппированных данных 
для сгруппированных данных 
Доверительный интервал для оценки математического ожидания нормального распределения при известном среднем квадратическом отклонении.
Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего  оценить ее математическое ожидание а. Будем рассматривать выборочное среднее
оценить ее математическое ожидание а. Будем рассматривать выборочное среднее  как случайную величину
как случайную величину  а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М(
а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М( ) = а,
) = а,  . Оценим вероятность выполнения неравенства
. Оценим вероятность выполнения неравенства  . Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
р (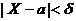 ) = 2F
) = 2F  . Тогда, с учетом того, что
. Тогда, с учетом того, что  , р (
, р ( ) = 2F
) = 2F  =
=
=2F(t), где  . Отсюда
. Отсюда  , и предыдущее равенство можно переписать так:
, и предыдущее равенство можно переписать так:
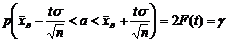 . (18.1)
. (18.1)
Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал  , где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2F(t) = γ.
, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2F(t) = γ.
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном среднем квадратическом отклонении.
Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания построим новую случайную величину
 , (18.2)
, (18.2)
где  - выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента (см. лекцию 12) с k = n – 1 степенями свободы.
- выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента (см. лекцию 12) с k = n – 1 степенями свободы.
Поскольку плотность распределения Стьюдента  , где
, где  , явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ, tγ), учитывая четность плотности распределения, следующим образом:
, явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ, tγ), учитывая четность плотности распределения, следующим образом:  . Отсюда получаем:
. Отсюда получаем:
 (18.3)
(18.3)
Таким образом, получен доверительный интервал для а, где tγ можно найти по соответствую-щей таблице при заданных п и γ.



 , которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований:
, которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований: ) она стремится к истинному значению параметра a.
) она стремится к истинному значению параметра a.

 оценить ее математическое ожидание а. Будем рассматривать выборочное среднее
оценить ее математическое ожидание а. Будем рассматривать выборочное среднее  а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М(
а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М( ) = а,
) = а,  . Оценим вероятность выполнения неравенства
. Оценим вероятность выполнения неравенства  . Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал: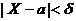 ) = 2F
) = 2F  . Тогда, с учетом того, что
. Тогда, с учетом того, что  ) = 2F
) = 2F  =
= . Отсюда
. Отсюда  , и предыдущее равенство можно переписать так:
, и предыдущее равенство можно переписать так: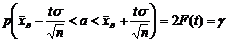 . (18.1)
. (18.1) , где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2F(t) = γ.
, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2F(t) = γ. , (18.2)
, (18.2) , где
, где  , явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ, tγ), учитывая четность плотности распределения, следующим образом:
, явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ, tγ), учитывая четность плотности распределения, следующим образом:  . Отсюда получаем:
. Отсюда получаем: (18.3)
(18.3)


