

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Билет 56)
Любое комплексное число (кроме нуля) 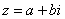 можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
 , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа.
Если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую, на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме  , то при его возведении в натуральную степень
, то при его возведении в натуральную степень  справедлива формула:
справедлива формула:
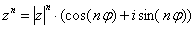
Теорема. (Формула корней из комплексного числа.)
Для любого ненулевого комплексного числа
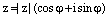 , где
, где  , существует ровно n корней n-й степени из комплексного числа z и все они могут быть найдены по формуле
, существует ровно n корней n-й степени из комплексного числа z и все они могут быть найдены по формуле
 ,
,
где  ,
,  – арифметический корень n-й степени из положительного числа
– арифметический корень n-й степени из положительного числа 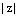 .
.
Билет 55)
Тригонометрической формой записи комплексного числа называют z = a + bi = r (cos φ + i sin φ).
Любое комплексное число состоит из двух частей: вещественной и мнимой:

Сложение.

1.2 Вычитание, аналогично, производится по следующему правилу:
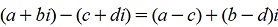 .
.
Умножение.

Деление.
Определяется просто как обратная операция к умножению.

Формула Муавра для комплексных чисел  утверждает, что
утверждает, что

для любого 
Билет 54)
Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:
| z 1 + z 2 = z 2 + z 1 |


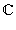 .
.| (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3) |

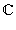 .
.| z + 0 = z |

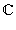 .
.| z 1 z 2 = z 2 z 1 |


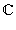 .
.| (z 1 z 2) z 3 = z 1(z 2 z 3) |


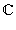 .
.| z 1(z 2 + z 3) = z 1 z 2 + z 1 z 3 |


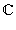 .
.| z · 1 = z. |
 и
и  существует такое число z, что
существует такое число z, что  Такое число z называется частным двух комплексных чисел и обозначается
Такое число z называется частным двух комплексных чисел и обозначается 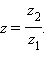 Деление на 0 невозможно.
Деление на 0 невозможно.Ко́мпле́ксные — расширение поля вещественных чисел, обычно обозначается. Любое комплексное число может быть представлено как формальная сумма, где и — вещественные числа, — мнимая единица.
|
|
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени с комплексными коэффициентами имеет ровно комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
Билет 52
Формулой Маклорена называется формула Тейлора при а = 0:



Билет 51)
РядТе́йлора — разложение функции в бесконечную сумму степенных функций.
Пусть функция  бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд
. Формальный ряд

называется рядом Тейлора функции  в точке
в точке  .
.
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
· Пусть функция  имеет имеет  производную в некоторой окрестности точки производную в некоторой окрестности точки  , , 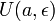 · Пусть
· Пусть  · Пусть
· Пусть  — произвольное положительное число,
тогда: — произвольное положительное число,
тогда:  точка точка  при при  или или  при при  : :

|
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
|
|
Билет 50)
Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).
Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий
 , , 
|
Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если 
Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если 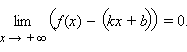 Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.
Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.
Билет 49)
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Пусть функция f(x) определена на интервале (a, b). Она
называется выпуклой вниз на интервале (a, b), если для любых точек x1 и x2,
a<x1 <x2 <b, и любых чисел α1 > 0 и α2 > 0 таких, что α1+α2 = 1, выполняется
неравенство
f(α1x1 + α2x2) 6 α1f(x1) + α2f(x2). (2.12.1)
Если для функции f справедливо обратное неравенство, то функция f называется
выпуклой вверх.
Всякий интервал, на котором функция выпукла вниз или
вверх, называется интервалом выпуклости функции.
Пусть функция f (x) непрерывна в точке 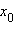 и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 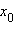 называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.
называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.
Необходимое условие наличия точки перегиба. Если 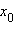 – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
– точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то

|
Билет 48)
Если производная некоторой непрерывной функции f(x) на некотором промежутке положительна (f'(x)>0), то на этом промежутке функция возрастает.
Если производная некоторой непрерывной функции f(x) на некотором промежутке отрицательна (f'(x)<0), то на этом промежутке функция убывает.
Эти условия являются достаточными условиями возрастания (убывания функции).
Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности  ,
,  , некоторой точки
, некоторой точки  своей области определения. Точка
своей области определения. Точка  называется точкой локального максимума, если в некоторой такой окрестности
называется точкой локального максимума, если в некоторой такой окрестности  выполняется неравенство
выполняется неравенство  (
( ), и точкой локального минимума, если
), и точкой локального минимума, если 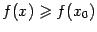
 .
.
|
|
Билет 47)
Правило Бернулли-Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида  и
и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1.  или
или  ;
;
2.  и
и  дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности  ;
;
3.  в проколотой окрестности
в проколотой окрестности  ;
;
4. существует  ,
,
тогда существует 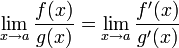 .
.
Пределы также могут быть односторонними

Билет 46)
Пусть 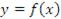 – некоторая дифференцируемая функция, производная от которой
– некоторая дифференцируемая функция, производная от которой  также является дифференцируемой функцией. Производная функции
также является дифференцируемой функцией. Производная функции  обозначается символическим выражением
обозначается символическим выражением  и называется второй производной (или производной второго порядка) функции
и называется второй производной (или производной второго порядка) функции  :
:
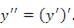
Запись вида

позволяет указать в явной форме переменную, по которой выполняется дифференцирование функции. Однако такое обозначение является достаточно громоздким и поэтому обычно используется его сокращенная форма:

Во многих задачах функция y (x) задана неявным образом. Например, для приведенных ниже функций

невозможно получить зависимость y (x) в явном виде.
Алгоритм вычисления производной y' (x) от неявной функции выглядит следующим образом:
Производную функции  , заданной параметрически, можно выразить через производные функций
, заданной параметрически, можно выразить через производные функций  и
и  : поскольку
: поскольку  и, по формуле производной обратной функции,
и, по формуле производной обратной функции,  , то
, то

где  -- значение параметра, при котором получается интересующее нас при вычислении производной значение
-- значение параметра, при котором получается интересующее нас при вычислении производной значение  .
.
Билет 45)
Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если
f(a) = f(b)
то внутри интервала [а, b] найдется хотя бы одно такое значение x0 (a < x0 < b), что
f ' (x0) = 0.
Доказательство.
Функция f(x) постоянна на интервале [ а, b ]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически.
|
|
Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [ а, b ] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x0 (a < x0 < b), что
f(b) - f(a) = (b - a)f '(x).
Теорема Коши о среднем значении является обобщением теоремы Лагранжа о конечных приращениях.
Пусть даны две функции  и
и 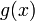 такие, что:
такие, что:
1.  и
и 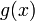 определены и непрерывны на отрезке
определены и непрерывны на отрезке  ;
;
2. производные  и
и  конечны на интервале
конечны на интервале 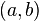 ;
;
3. производные  и
и  не обращаются в нуль одновременно на интервале
не обращаются в нуль одновременно на интервале 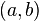
4.  ;
;
тогда существует  , для которой верно:
, для которой верно:
 .
.
(Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале  .)
.)
Доказательство
Для доказательства введём функцию

|
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны  . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции  равна нулю, а
равна нулю, а  равна как раз необходимому числу.
равна как раз необходимому числу.
Если х - независимая переменная и y = f(x) - дифференцируемая функция, то dx = f'(x)dx, т. е. дифференциал функции есть функция, зависящая от двух аргументов х и dx. Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом).
Считая dx постоянной, получаем, что df(x) - функция одной переменной. Предположим, что функция у = f(x) имеет не только первую производную, но и n последовательных производных y" = f"(x), y’” = f”’(x).
Дифференциал от дифференциала функции у = f{x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y = d(dy), причем

Дифференциалом n-го порядка

Смотрите пример вычисления дифференциалов первого и второго порядков
Инвариантность формы дифференциала
Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда 
Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала (7), когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.
Билет 43
Если у есть неявная функция от х, т.е. задана уравнением F(x,y)=0, не разрешенным относительно у, то для нахождения производной нужно продифференцировать по х обе части равенства, помня, что у есть функция от х, и затем разрешить полученное равенство относительно у'.
Пример. Найти производную неявной функции х2+у2-4х-10у+4=0.
Дифференцируя по х, получаем 2х+2у *у' -4-10у'=0. Выражаем у', имеем:

Функция задана параметрически, если зависимость функции y от аргумента x задана посредством параметра t:

Производная параметрической функции равна частному производных y и x, взятых по переменной t:
|
|

или в других обозначениях
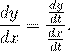
Билет 42
Билет 41)
Пусть функция f(x) определена на промежутке (a; b),  и
и  - точки этого промежутка. Производной функции f(x) в точке
- точки этого промежутка. Производной функции f(x) в точке  называется предел отношения приращения функции к приращению аргумента при
называется предел отношения приращения функции к приращению аргумента при  . Обозначается
. Обозначается  .
.
Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке  , то есть, мы имеем возможность определить новую функцию
, то есть, мы имеем возможность определить новую функцию  , которую называют производной функции f(x) на интервале (a; b).
, которую называют производной функции f(x) на интервале (a; b).
Билет 56)
Любое комплексное число (кроме нуля) 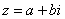 можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
 , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа.
Если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую, на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме  , то при его возведении в натуральную степень
, то при его возведении в натуральную степень  справедлива формула:
справедлива формула:
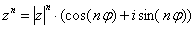
Теорема. (Формула корней из комплексного числа.)
Для любого ненулевого комплексного числа
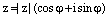 , где
, где  , существует ровно n корней n-й степени из комплексного числа z и все они могут быть найдены по формуле
, существует ровно n корней n-й степени из комплексного числа z и все они могут быть найдены по формуле
 ,
,
где  ,
,  – арифметический корень n-й степени из положительного числа
– арифметический корень n-й степени из положительного числа 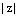 .
.
Билет 55)
Тригонометрической формой записи комплексного числа называют z = a + bi = r (cos φ + i sin φ).
Любое комплексное число состоит из двух частей: вещественной и мнимой:

Сложение.

1.2 Вычитание, аналогично, производится по следующему правилу:
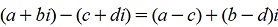 .
.
Умножение.

Деление.
Определяется просто как обратная операция к умножению.

Формула Муавра для комплексных чисел  утверждает, что
утверждает, что

для любого 
Билет 54)
Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:
| z 1 + z 2 = z 2 + z 1 |


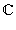 .
.| (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3) |

 .
.| z + 0 = z |

 .
.| z 1 z 2 = z 2 z 1 |


 .
.| (z 1 z 2) z 3 = z 1(z 2 z 3) |


 .
.| z 1(z 2 + z 3) = z 1 z 2 + z 1 z 3 |


 .
.| z · 1 = z. |
 и
и  существует такое число z, что
существует такое число z, что  Такое число z называется частным двух комплексных чисел и обозначается
Такое число z называется частным двух комплексных чисел и обозначается 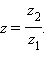 Деление на 0 невозможно.
Деление на 0 невозможно.Ко́мпле́ксные — расширение поля вещественных чисел, обычно обозначается. Любое комплексное число может быть представлено как формальная сумма, где и — вещественные числа, — мнимая единица.
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени с комплексными коэффициентами имеет ровно комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
Напр.: комплексные числа используются в электротехнике для расчёта цепей переменного тока.
Форма записи z= x+iy комплексных чисел называется декартовой. Она равносильна представлению комплексных чисел, как точек плоскости в декартовой системе координат, где числу z= x+iy соответствует точка М с координатами (x; y).
Такое представление комплексных чисел называется геометрической интерпретацией комплексных чисел, а плоскость, точкам которой сопоставлены комплексные числа – комплексной плоскостью.
Всякое комплексное число z=x+ i y можно изобразить точкой М(х;у) плоскости ОXY такой, что х=Rez, у=Imz. И, наоборот, каждую точку М(х;у) координатной плоскости можно рассматривать как образ комплексного числа z=х+ i y (см. рис. 161).
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=х+0 i =х. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+ i y.

Комплексное число z=х+ i y можно задавать с помощью радиус-вектора r=ОМ=(х;у). Длина вектора r, изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r. Величина угла между положительным направлением действительной оси и вектором r, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Argz или φ.
Аргумент комплексного числа z=0 не определен. Аргумент комплексного числа z≠0 — величина многозначная и определяется с точностью до слагаемого 2πk (k=0,-1,1,-2,2...): Argz = argz + 2πk, где argz — главное значение аргумента, заключенное в промежутке (—π;π], т. е. —π<argz≤π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2π)).
http://mathematics.uni-dubna.ru/matherials/arbuzova/ma/Lecture2-1.pdf
Билет 52
Формулой Маклорена называется формула Тейлора при а = 0:



Билет 51)
РядТе́йлора — разложение функции в бесконечную сумму степенных функций.
Пусть функция  бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд
. Формальный ряд

называется рядом Тейлора функции  в точке
в точке  .
.
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
· Пусть функция  имеет имеет  производную в некоторой окрестности точки производную в некоторой окрестности точки  , , 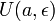 · Пусть
· Пусть  · Пусть
· Пусть  — произвольное положительное число,
тогда: — произвольное положительное число,
тогда:  точка точка  при при  или или  при при  : :

|
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!