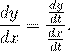Из леммы Ферма вытекает следующее:
Пусть точка  является точкой экстремума функции
является точкой экстремума функции 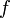 , определенной в некоторой окрестности точки
, определенной в некоторой окрестности точки  .
.
Тогда либо производная  не существует, либо
не существует, либо 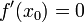 .
.
Достаточные условия существования локальных экстремумов
· Пусть функция 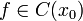 непрерывна в
непрерывна в 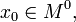 и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные 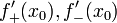 . Тогда при условии
. Тогда при условии

 является точкой строгого локального максимума. А если
является точкой строгого локального максимума. А если
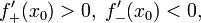
то  является точкой строгого локального минимума.
является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке 
· Пусть функция  непрерывна и дважды дифференцируема в точке
непрерывна и дважды дифференцируема в точке  . Тогда при условии
. Тогда при условии
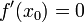 и
и 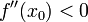
 является точкой локального максимума. А если
является точкой локального максимума. А если
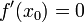 и
и 
то  является точкой локального минимума.
является точкой локального минимума.
· Пусть функция  дифференцируема
дифференцируема 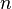 раз в точке
раз в точке  и
и 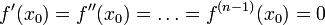 , а
, а 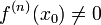 .
.
Если 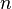 чётно и
чётно и 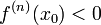 , то
, то  - точка локального максимума. Если
- точка локального максимума. Если 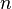 чётно и
чётно и 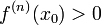 , то
, то  - точка локального минимума. Если
- точка локального минимума. Если 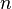 нечётно, то экстремума нет.
нечётно, то экстремума нет.
Билет 47)
Правило Бернулли-Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида  и
и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1.  или
или  ;
;
2.  и
и  дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности  ;
;
3.  в проколотой окрестности
в проколотой окрестности  ;
;
4. существует  ,
,
тогда существует 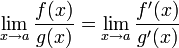 .
.
Пределы также могут быть односторонними

Билет 46)
Пусть 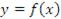 – некоторая дифференцируемая функция, производная от которой
– некоторая дифференцируемая функция, производная от которой  также является дифференцируемой функцией. Производная функции
также является дифференцируемой функцией. Производная функции  обозначается символическим выражением
обозначается символическим выражением  и называется второй производной (или производной второго порядка) функции
и называется второй производной (или производной второго порядка) функции  :
:
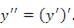
Запись вида

позволяет указать в явной форме переменную, по которой выполняется дифференцирование функции. Однако такое обозначение является достаточно громоздким и поэтому обычно используется его сокращенная форма:

Во многих задачах функция y (x) задана неявным образом. Например, для приведенных ниже функций

невозможно получить зависимость y (x) в явном виде.
Алгоритм вычисления производной y' (x) от неявной функции выглядит следующим образом:
- Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая,
что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции; - Решить полученное уравнение относительно производной y' (x).
Производную функции  , заданной параметрически, можно выразить через производные функций
, заданной параметрически, можно выразить через производные функций  и
и  : поскольку
: поскольку  и, по формуле производной обратной функции,
и, по формуле производной обратной функции,  , то
, то

где  -- значение параметра, при котором получается интересующее нас при вычислении производной значение
-- значение параметра, при котором получается интересующее нас при вычислении производной значение  .
.
Билет 45)
Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если
f(a) = f(b)
то внутри интервала [а, b] найдется хотя бы одно такое значение x0 (a < x0 < b), что
f ' (x0) = 0.
Доказательство.
Функция f(x) постоянна на интервале [ а, b ]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически.
Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [ а, b ] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x0 (a < x0 < b), что
f(b) - f(a) = (b - a)f '(x).
Теорема Коши о среднем значении является обобщением теоремы Лагранжа о конечных приращениях.
Пусть даны две функции  и
и 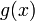 такие, что:
такие, что:
1.  и
и 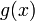 определены и непрерывны на отрезке
определены и непрерывны на отрезке  ;
;
2. производные  и
и  конечны на интервале
конечны на интервале 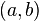 ;
;
3. производные  и
и  не обращаются в нуль одновременно на интервале
не обращаются в нуль одновременно на интервале 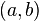
4.  ;
;
тогда существует  , для которой верно:
, для которой верно:
 .
.
(Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале  .)
.)
Доказательство
Для доказательства введём функцию
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны  . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции  равна нулю, а
равна нулю, а  равна как раз необходимому числу.
равна как раз необходимому числу.
Если х - независимая переменная и y = f(x) - дифференцируемая функция, то dx = f'(x)dx, т. е. дифференциал функции есть функция, зависящая от двух аргументов х и dx. Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом).
Считая dx постоянной, получаем, что df(x) - функция одной переменной. Предположим, что функция у = f(x) имеет не только первую производную, но и n последовательных производных y" = f"(x), y’” = f”’(x).
Дифференциал от дифференциала функции у = f{x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y = d(dy), причем

Дифференциалом n-го порядка

Смотрите пример вычисления дифференциалов первого и второго порядков
Инвариантность формы дифференциала
Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда 
Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала (7), когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.
Билет 43
Если у есть неявная функция от х, т.е. задана уравнением F(x,y)=0, не разрешенным относительно у, то для нахождения производной нужно продифференцировать по х обе части равенства, помня, что у есть функция от х, и затем разрешить полученное равенство относительно у'.
Пример. Найти производную неявной функции х2+у2-4х-10у+4=0.
Дифференцируя по х, получаем 2х+2у *у' -4-10у'=0. Выражаем у', имеем:

Функция задана параметрически, если зависимость функции y от аргумента x задана посредством параметра t:

Производная параметрической функции равна частному производных y и x, взятых по переменной t:

или в других обозначениях
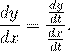
Билет 42



 является точкой экстремума функции
является точкой экстремума функции 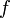 , определенной в некоторой окрестности точки
, определенной в некоторой окрестности точки  не существует, либо
не существует, либо 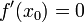 .
.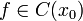 непрерывна в
непрерывна в 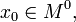 и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные 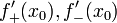 . Тогда при условии
. Тогда при условии
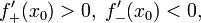
 непрерывна и дважды дифференцируема в точке
непрерывна и дважды дифференцируема в точке 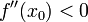

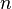 раз в точке
раз в точке 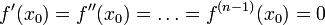 , а
, а 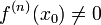 .
.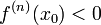 , то
, то 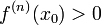 , то
, то  и
и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных. или
или  ;
; и
и  дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности  ;
; в проколотой окрестности
в проколотой окрестности  ,
,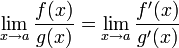 .
.
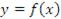 – некоторая дифференцируемая функция, производная от которой
– некоторая дифференцируемая функция, производная от которой  также является дифференцируемой функцией. Производная функции
также является дифференцируемой функцией. Производная функции  обозначается символическим выражением
обозначается символическим выражением  и называется второй производной (или производной второго порядка) функции
и называется второй производной (или производной второго порядка) функции  :
: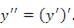



 , заданной параметрически, можно выразить через производные функций
, заданной параметрически, можно выразить через производные функций  и
и  : поскольку
: поскольку  и, по формуле производной обратной функции,
и, по формуле производной обратной функции,  , то
, то
 -- значение параметра, при котором получается интересующее нас при вычислении производной значение
-- значение параметра, при котором получается интересующее нас при вычислении производной значение  .
. такие, что:
такие, что: ;
; и
и  конечны на интервале
конечны на интервале  ;
; ;
; , для которой верно:
, для которой верно: .
. .)
.)
 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции  равна нулю, а
равна нулю, а  равна как раз необходимому числу.
равна как раз необходимому числу.