Большинство итерационных алгоритмов определения максимума или минимума функции, как одной, так и нескольких переменных, применяются для определения локального максимума (минимума). «Локальный максимум (минимум)» означает, что в рассматриваемой области должен быть только один максимум или минимум. «Найти максимум или минимум» означает вычислить максимальное или минимальное значаение функции и значение аргумента.
Математическим условием максимума или минимума функции f(х) в точке х0 является равенство нулю первой производной данной функции в точке х0.
Численно посчитать значение первой производной некоторой функции можно по следующим разностным формулам:
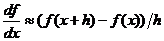 (1)
(1)
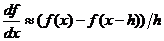 (2)
(2)
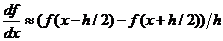 . (3)
. (3)
Формула (1) – разностаная формула для производной «разность вперед», (2) – разностная формула для производной «разность назад», (3) – разностная формула для производной «центральная разность».
В точке максимума или минимума функции ее производная равна нулю. Более того, знак производной функции определяет характер поведения функции в любой данной точке: если производная положительна – функция возрастает, если производная отрицательна – функция убывает.
Чтобы определить примерное расположение интересующего нас максимума (минимума) можно использовать табулирование функции или основанные на табулировании методы прямого перебора значений функции на некоторой сетке аргумента (или аргументов, в случае многомерной функции).
Простейшие методы определения максимума или минимума основываются на построении таблицы значений разностной производной исследуемой функции и определении координат нуля производной. Чаще всего используется формула (1). Точность определения максимума или минимума функции определяется величиной шага при определении разностной производной, чем меньше шаг – тем точнее локализован максимум или минимум.
На практике при табулировании функции точный ноль производной получить практически невозможно. Поэтому ноль производной вычисляют с некоторой допустимой погрешностью как разницу между ближайшими близкими к нулю положительным и отрицательным значениями производной в данной точке. При этом погрешность может быть учтена как для значений производной функции (по оси Y), так и для значения координаты точки (по оси Х).
Рассмотрим функцию одной переменной f(x). Пусть эта функция имеет максимум fm=f(xm) в точке xm на отрезке a<x<b.
Описание алгоритма определения максимального (минимального) значения функции одной переменной методом последовательного перебора:
Задаем начальные значения рабочего шага h0, точность определения максимума (минимума) d, начального значения аргумента функции x0.
Вычисляем значение функции в начальной точке f0=f(x0).
В цикле вычисляем:
новое приближение х: x 1= x0 + d;
новое значение функции f 1 в точке x1;
производную функции df =(f 1 -f0)/(x 1 -x0);
в соответствии со знаком производной определяем рабочий шаг h =знак(df)× h0;
если производная меньше нуля, то рабочий шаг h будет равен:– h0;
если значение функции в начальной точке f0 меньше значения функции в следующей f 1точке и если h0 меньше шага d, то максимум найден,
иначе делим h0 пополам и продолжаем вычисления в цикле.
Если цикл завершен, то печатать сообщение, что максимум (минимум) не найден.
Алгоритм определения максимального (минимального) значения функции одной переменной методом последовательного перебора на естественном языке:
d=0.01
x0=0.5
h0=1
max_k=10000
f0=функция(x0)
Цикл по k от 1 до max_k
x1=x0+d
f1=функция(x1)
df=(f1-f0)/(x1-x0)
h=знак(df)*h0
x0=x0+h
f0=функция(x0)
Если f0<f1 то
Если h0<d то
Печать "Максимум x0=", x0
Печать " f0= ", f0," x1=",x1, " f1=", f1
Выход Из Программы
Конец Если
h0=h0/5
Конец Если
Конец Цикла
Печать "Максимум не найден"
ОПРЕДЕЛЕНИЕ ФУНКЦИИ функция
Параметр x
Возврат -10*(x-20)*(x-400)
Обозначяение знак(df) в данном алгоритме – стандартная функция, возвращающая знак своего аргумента.
Пример решения на языке VFP:
_screen.FontSize = 10
clear
d=0.01
x0=0.5
h0=1
f0=функция(x0)
FOR k=1 TO 10000
x1=x0+d
f1=функция(x1)
df=(f1-f0)/(x1-x0)
h=SIGN(df)*h0
x0=x0+h
f0=функция(x0)
IF f0<f1
IF h0<d
? "Максимум x0=", x0, " f0= ", f0," x1=",x1, " f1=", f1
RETURN
endif
h0=h0/5
ENDIF
endfor
? "Максимум не найден"
FUNCTION функция
LPARAMETERS x
RETURN -10*(x-20)*(x-40)
Пример решения на языке VBA:
Sub maxf()
d = 0.01
x0 = 0.5
h0 = 1
f0 = функция(x0)
For k = 1 To 10000
x1 = x0 + d
f1 = функция (x1)
df = (f1 - f0) / (x1 - x0)
h = Sgn(df) * h0
x0 = x0 + h
f0 = функция (x0)
If f0 < f1 Then
If h0 < d Then
Debug.Print "Максимум найден за " & k & " итераций!"
Debug.Print "x0= " & x0 & ": f0= " & f0 & ": x1= " & x1 & ": f1= " & f1
Exit Sub
End If
h0 = h0 / 5
End If
Next
Debug.Print "Максимум не найден"
End Sub
Function функция (x)
функция = -10 * (x - 20) * (x - 40)
End Function
Результат работы программы на VBA:
Максимум найден за 42 итераций!
x0= 29,988: f0= 999,99856: x1= 30,006: f1= 999,99964
Определение максимального и минимального значения функции двух переменных методом градиентного спуска (подъема)
В случае многомерных функций поиск максимального или минимального значений функции ведется на координатной сетке, заданной количеством измерений координат функции. Для двумерной функции f(x,y) координатной сеткой будет плоскость (x,y), для функции трех переменных f(x,y,z) сеткой будет пространство (x,y,z) и т.д.
Для многомерного случая в качастве аналога производной используется понятие «градиента».
Градиентом функции называется вектор, компоненты которого являются частными производными функции по соответствующим координатам. Так, например, для функции двух переменных f(x,y) градиент определяется как вектор с компонентами: 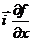 и
и 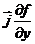 . Обозначается градиент функции
. Обозначается градиент функции  либо без значка вектора.
либо без значка вектора.
Градиент функции f(x1, x2,..., xn) в каждой точке направлен в сторону наискорейшего локального возрастания этой функции. Для поиска минимума необходимо двигаться в направлении противоположном градиенту функции.
При численных расчетах градиент функции можно определить приближенно 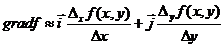 , где
, где 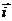 ,
, 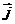 – единичные вектора по направлениям осей X и Y,
– единичные вектора по направлениям осей X и Y, 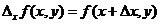 ,
, 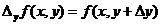 ,
, 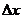 – приращение x,
– приращение x, 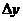 – приращение y.
– приращение y.
Вектор градиента 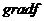 указывает, подобно производной одномерной функции, направление на ближайший локальный максимум функции в данной точке, вектор
указывает, подобно производной одномерной функции, направление на ближайший локальный максимум функции в данной точке, вектор 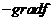 – направление на ближайший локальный минимум.
– направление на ближайший локальный минимум.
Метод определения максимума (минимума) функции, основанный на вычислении градиента функции называется методом наискорейшего подъема (спуска). В данном итерационном методе вектор шага определяется направлением вектора градиента:
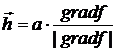 . (4)
. (4)
Параметр а, определяет длину шага в направлении подъема, а также этот параметр определяет погрешность нахождения максимума (минимума) на сетке. Чем меньше значения параметра а, тем точнее вычисляются значения максимума (минимума). С другой стороны, при малых значениях параметра а итерационный процесс будет продолжаться достаточно долго. Поэтому можно использовать следующий прием: на первом этапе находим максимум (минимум) при относительно больших значениях параметра а, далее, из ближайшей точки повторяем итерации и при уменьшении значения модуля градиента (т.е. мы двигаемся в нужном направлении) дробим значения параметра а до достижения необходимой точности вычислений. Условие останова данного итерацеонного метода заключается в том, что модуль градиента в формуле (4) будет точно равен нулю в точке максимума (минимума). Поэтому достаточно вычислить значение модуля градиента близкое к нулю с некоторой погрешностью.
Рассмотрим многомерную функцию, имеющую вид колокола:
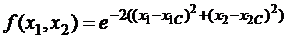 , (5)
, (5)
где точка 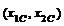 – точка максимума функции.
– точка максимума функции.
В области изменений 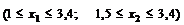 функция имеет вид:
функция имеет вид:
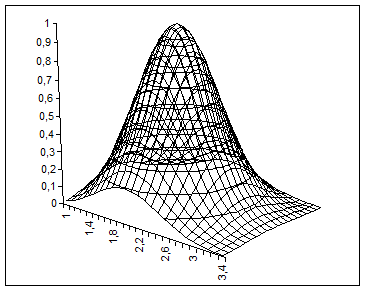
Аналогичные функции можно построить в многомерном пространстве. Например, если размерность пространства n, то функция «n-мерный колокол» будет иметь вид:
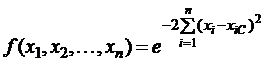 . (6)
. (6)
Точка максимума этой функции - 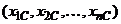 . Функция «n-мерного колокола» (6) при n=2 превращается в (5).
. Функция «n-мерного колокола» (6) при n=2 превращается в (5).
Описание алгоритма нахождения максимального (минимального) значения функции двух переменных методом градиентного спуска (подъема):
Задаем размерность n массива аргументов минимизируемой (максимизируемой) многомерной функции, погрешность вычислений ε , начальные значения шага d по X и Y, координаты начальной точки поиска x0, y0, определяем вспомогательный массив для запоминания значений аргументов при дроблении шага х1, y1, массив для составляющих градиента функции df.
Вычисляем значение функции в точке с координатами (x0, y0).
Вычисляем х и y компоненты вектора градиента функции по формулам:
gx=(f(x0+dx, y0)-f(x0,y0))/dx;
gy=(f(x0, y0+dy)-f(x0,y0))/dy.
Вычисляем модуль градиента функции.
Вычисляем новое значение функции и сравниваем с предыдущим. Если максимум (минимум) не найден, продолжаем итерации.
Если второе условие не выполнилось, уменьшаем шаг.
Алгоритм на естественном языке приведем для функции «n-мерного колокола».
Строки «комментарии» будем начинать с символа «*».
Для функции с координатами точки максимума: (2, 3, 4, …, n+1) для пространства размерности n.
Определить n как целое, где n – количество аргументов функции.
n=2
Определить массивы x0(n), x1(n), x2(n), df(n), h(n)
* массивы x0, x1, х2 – рабочие массивы координат точек (0), (1),
* (2). Массивы df – компоненты вектора градиента функции,
* h – компоненты векторов шага
Определить глобальный массив xс(n)
* массив xс-массив координат точки максимума функции
eps=0.01
d=0.01
* в данном цикле задаются координаты точки максимума
Цикл по i от 1 до n
xc(i)=1+i
Конец Цикла
* здесь задаются координаты начальной точки для определения
* максимума
Цикл по i от 1 до n
x0(i)=0.1+i
Конец Цикла
h0=0.5
f0=колокол(@x0,n)
Цикл по k от 1 до 10000
Печать "k=",x0(1),x0(2),f0,h0
Цикл по j от 1 до n
Цикл по i от 1 до n
x1(i)=x0(i)
Конец Цикла
x1(j)=x0(j)+d
f1=колокол(@x1,n)
df(j)=(f1-f0)/d
Конец Цикла
* нормирование градиента
lendf=0
Цикл по i от 1 до n
lendf = lendf + df(i)^2
Конец Цикла
lendf = Корень(lendf)
Цикл по i от 1 до n
df(i)=df(i)/lendf
Конец Цикла
Цикл по i от 1 до n
x0(i)=x0(i)+df(i)*h0
Конец Цикла
f0_1=колокол(@x0,n)
Если f0_1=<f0
Печать " нашли max"
Если h0<eps
Печать "найден max x0=(",
Цикл по i от 1 до n
Печать x0(i)
Конец Цикла
Печать ")"
Печать " f0= ", f0
Печать "за ",k," итераций"
Выход Из Программы
Конец Если
h0=h0/2
Конец Если
f0=f0_1
Конец Цикла
Печать "максимум не найден x="
Цикл по i от 1 до n
Печать x0(i)
Конец Цикла
ОПРЕДЕЛИТЬ ФУНКЦИЮ колокол
Параметры x, n
определить массив x(n)
определить локальную переменную r2
r2=0
Цикл по i от 1 до n
r2=r2+(x(i)-xc(i))^2
Конец Цикла
Если r2>10
r2=10
Конец Если
Вернуть 5*(EXP(-0.1*r2))
Пример решения на языке VFP:
CLEAR
SET DECIMALS TO 15
n=10
DIMENSION x0(n), x1(n), df(n), h(n), x2(n)
PUBLIC ARRAY xc(n)
FOR i=1 TO n
xc(i)=1+i
ENDFOR
eps=0.01
d=0.01
FOR i=1 TO n
x0(i)=1.1+i
ENDFOR
h0=0.5
f0=функция(@x0,n)
FOR k=1 TO 10000
? "k=",STR(x0(1),5,2),STR(x0(2),5,2),f0,h0
FOR j=1 TO n
FOR i=1 TO n
x1(i)=x0(i)
ENDFOR
x1(j)=x0(j)+d
f1=функция(@x1,n)
df(j)=(f1-f0)/d
ENDFOR
* нормирование градиента
lendf=0
FOR i=1 TO n
lendf = lendf + df(i)^2
ENDFOR
lendf = SQRT(lendf)
FOR i=1 TO n
df(i)=df(i)/lendf
ENDFOR
FOR i=1 TO n
x0(i)=x0(i)+df(i)*h0
ENDFOR
f0_1=функция(@x0,n)
IF f0_1=<f0
? " нашли max"
IF h0<eps
? "найден max x0=(",
FOR i=1 TO n
??x0(i)
ENDFOR
??")"
?" f0= ", f0
? "за ",k," итераций"
RETURN
endif
h0=h0/2
ENDIF
f0=f0_1
endfor
? "максимум не найден x="
FOR i=1 TO n
??x0(i)
ENDFOR
FUNCTION функция
LPARAMETERS x, n
DIMENSION x(n)
LOCAL r2
r2=0
FOR i=1 TO n
r2=r2+(x(i)-xc(i))^2
ENDFOR
IF r2>10
r2=10
ENDIF
RETURN 5*(EXP(-0.1*r2))
Пример решения на языке VBA:
'объявление глобального массива xc() неопределенной длины
Public xc()
Sub grd()
Dim x0(), x1(), df(), h(), x2()
n = 10
ReDim x0(n), x1(n), df(n), h(n), x2(n)
ReDim xc(n)
For i = 1 To n
xc(i) = 1 + i
Next
eps = 0.01
d = 0.01
For i = 1 To n
x0(i) = 1.1 + i
Next
h0 = 0.5
f0 = f2(x0, n)
For k = 1 To 10000
Debug.Print "k= " & k & ": " & x0(1) & ": " & x0(2) & ": " & f0 & ": " & h0
For j = 1 To n
For i = 1 To n
x1(i) = x0(i)
Next
x1(j) = x0(j) + d
f1 = f2(x1, n)
df(j) = (f1 - f0) / d
Next
' нормирование градиента
lendf = 0
For i = 1 To n
lendf = lendf + df(i) ^ 2
Next
lendf = Sqr(lendf)
For i = 1 To n
df(i) = df(i) / lendf
Next
For i = 1 To n
x0(i) = x0(i) + df(i) * h0
Next i
f0_1 = f2(x0, n)
If f0_1 <= f0 Then
If h0 < eps Then
s = ""
For i = 1 To n - 1
s = s & x0(i) & ","
Next i
s = s & x0(n)
Debug.Print "Максимум найден за " & k & " итераций!"
Debug.Print "x0=(" & s & ")"
Debug.Print "f0= " & f0
Exit Sub
End If
h0 = h0 / 2
End If
f0 = f0_1
Next k
Debug.Print "максимум не найден!"
End Sub
Function f2(ByRef x, n)
Dim r2
r2 = 0
For i = 1 To n
r2 = r2 + (x(i) - xc(i)) ^ 2
Next
If r2 > 10 Then
r2 = 10
End If
f2 = 5 * (Exp(-0.1 * r2))
End Function
Результат работы программы на VBA:
k= 1: 2,1: 3,1: 4,95024916874584: 0,5
k= 2: 1,94188611699158: 2,94188611699158: 4,98314236503072: 0,5
k= 3: 2,1: 3,1: 4,95024916874584: 0,25
k= 4: 2,02094305849579: 3,02094305849579: 4,99780742238446: 0,25
k= 5: 1,94188611699158: 2,94188611699158: 4,98314236503072: 0,125
k= 6: 1,98141458774369: 2,98141458774369: 4,99827321050518: 0,125
k= 7: 2,02094305849579: 3,02094305849579: 4,99780742238446: 0,0625
k= 8: 2,00117882311974: 3,00117882311974: 4,99999305188509: 0,0625
k= 9: 1,98141458774369: 2,98141458774369: 4,99827321050518: 0,03125
k= 10: 1,99129670543171: 2,99129670543171: 4,99962127766207: 0,03125
k= 11: 2,00117882311974: 3,00117882311974: 4,99999305188509: 0,03125
k= 12: 1,99129670543171: 2,99129670543171: 4,99962127766207: 0,015625
k= 13: 1,99623776427573: 2,99623776427573: 4,99992922841264: 0,015625
k= 14: 1,99129670543171: 2,99129670543171: 4,99962127766207: 0,0078125
k= 15: 1,99376723485372: 2,99376723485372: 4,9998057669659: 0,0078125
k= 16: 1,99623776427565: 2,99623776427565: 4,99992922841264: 0,0078125
Максимум найден за 16 итераций!
x0=(1,99376723485379; 2,99376723485379; 3,99376723485379; 4,99376723485379; 5,99376723485379; 6,99376723485379; 7,99376723485361; 8,99376723485361; 9,99376723485361; 10,9937672348536)
f0= 4,99992922841264
Контрольные вопросы
1. Дать определение функции одной переменной. Привести примеры функции одной переменной.
2. Дать определение функции двух переменных. Привести примеры функции двух переменных.
3. Дать определение экстремума функции.
4. Дать определение максимума, минимума функции.
5. Дать определение локального максимума, минимума функции.
6. Дать определение глобального максимума, минимума функции.
7. Дать определение монотонности функции.
8. Объяснить процедуру определения направления роста функции.
9. Дать определение производной функции.
10. Графический смысл производной функции.
11. Дать понятие разностной производной.
12. Получить формулу определения знака шага процедуры определения максимума/минимума функции методом последовательного перебора.
13. Объяснить алгоритм определения максимума/минимума функции методом последовательного перебора.
14. Дать определение точности нахождения максимума/минимума функции.
15. Объяснить алгоритм определения максимума/минимума функций специального вида («полочка», «ступенька»).
16. Дать определение градиента функции нескольких переменных.
17. Получить разностную формулу градиента функции.
18. Дать численное определение х-компоненты вектора градиента функции.
19. Объяснить, что такое направление градиента вектора функции.
20. Объяснить алгоритм метода градиентного спуска, подъема.
21. Дать определение гладкой и разрывной функции.
22. Что является критерием окончания итерационного процесса метода градиентного спуска (подъема)?
Задания
1. Проанализировать поведение функции, построить график, приближенно определить положение максимума или минимума функции. Найти максимум (минимум) заданной функции одной переменной численным методом. Точность определения экстремума задать самостоятельно:
1. f (x)=(x+ 1)2/ (x –1)
2. f (x)=(x+ 1)3/ (x –1)2
3. f (x)=2 x 2 – x 4
4. f (x)=0,1 x 3 – 2 x 2 + 10 x
5. f (x)=(x 2 + 1) /(x ‑ 1)
6. f (x)=0,4 x 3 – 3 x 2 + 8 x
7. f (x)=0,1 x 3 – 2 +x 2 ‑ 10 x
8. f (x)=(2 x 2 + 1) / (x – 1)
9. f (x)= (x 2 + 3) / (x ‑ 1)
10. f (x)= (2 x 2 + 1) / (x ‑ 2)
11. f (x)=0,3 x 3 – 2 x 2 + 6 x
12. f (x)= x 3 – 6 x 2 + 9 x –4
13. f (x)= x (x –1)2(x– 2)
14. f (x)= x+ 1/ x
15. f (x)=2 x /(1 + x 2)
16. f (x)=(x 2 – 3 x+ 2)/(x 2 + 2 x+ 1)
17. f (x)=(2 x – x 2)1/2
18. f (x)= x (x– 1) 1/3
19. f (x)= xe – x
20. f (x)= x 1/2 ln (x)
21. f (x)= xln 2(x)
22. f (x)=cos(x) + 0.5 cos(2 x)
23. f (x)=10/(1+sin2 x)
24. f (x)= ex sin(x)
25. f (x)= x 2 – 4 x+ 6
26. f (x)=(5 – 4 x)1/2
27. f (x)=3 x – x 3
28. f (x)=(x – 2)(x 2 + 1)1/2
29. f (x)=2 x – tg(x)
30. f (x)=(x + 2) e 1/ x
31. f (x)=sin(x) + 1/3sin3 x
32. f (x)=(x 4 + 8)/(x 3 + 1)
33. f (x)=(x – 3) x 1/2
2. Построить график функции (поверхность), приближенно определить положение максимума или минимума функции. Найти максимум (минимум) заданной функции двух переменных методом градиентного спуска (подъема). Точность определения экстремума задать самостоятельно.
1. z(x,y)= x 2 + (y –1)2
2. z(x,y)= x 2 – (y –1)2
3. z(x,y)=(x – y+ 1)2
4. z(x,y)= x 2 – xy + y 2–2 x + y
5. z(x,y)= x 2 y 3(6– x – y)
6. z(x,y)= x 3 + y 3–3 xy
7. z(x,y)= x 4 + y 4– x 2–2 xy – y 2
8. z(x,y)=2 x 4 + y 4– x 2 –2 y 2
9. z(x,y)= x y +50/ x +50/ y
10. z(x,y)=1–(x 2+ y 2)1/2
11. z(x,y)= (5–2 x + y)exp(x 2– y)
12. z(x,y)=(8 x 2–6 xy +3 y 2) exp(2 x +3 y)
13. z(x,y)=(5 x +7 y –25) exp(–(x 2+ xy + y 2))
14. z(x,y)= x 2+ xy + y 2–4ln x –10ln y
15. z(x,y)=sin x +cos y +cos(x – y)
16. z(x,y)=sin x sin y sin(x + y)
17. z(x,y)= xy ln(x 2+ y 2)
18. z(x,y)= x + y +4 sin x sin y
19. z(x,y)=(x 2+ y 2) exp(– (x 2– y 2))
20. z(x,y)= x 2+2 y 2–ln(x + y 2)



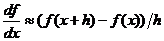 (1)
(1)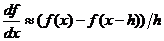 (2)
(2)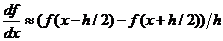 . (3)
. (3)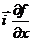 и
и 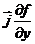 . Обозначается градиент функции
. Обозначается градиент функции  либо без значка вектора.
либо без значка вектора.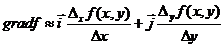 , где
, где 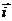 ,
, 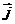 – единичные вектора по направлениям осей X и Y,
– единичные вектора по направлениям осей X и Y, 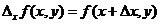 ,
, 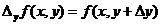 ,
, 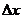 – приращение x,
– приращение x, 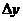 – приращение y.
– приращение y.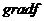 указывает, подобно производной одномерной функции, направление на ближайший локальный максимум функции в данной точке, вектор
указывает, подобно производной одномерной функции, направление на ближайший локальный максимум функции в данной точке, вектор 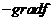 – направление на ближайший локальный минимум.
– направление на ближайший локальный минимум.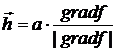 . (4)
. (4)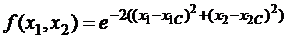 , (5)
, (5)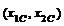 – точка максимума функции.
– точка максимума функции.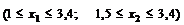 функция имеет вид:
функция имеет вид:
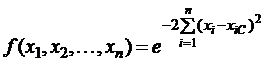 . (6)
. (6)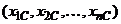 . Функция «n-мерного колокола» (6) при n=2 превращается в (5).
. Функция «n-мерного колокола» (6) при n=2 превращается в (5).


