| Обозначение элемента по схеме и его тип
| Интенс. отказов
 ,
отк / час ,
отк / час
|  , ,
| Коэф-т нагрузки

| Поправ.
коэф-т

| 
 отк / час
отк / час
|
| Микросхемы
А1 К2УС241
...........
Конденсаторы
С1 КМ-5а-Н90-0,068
мкФ
С2 КМ-4а-М750-510 пФ
...........
Резисторы
R1 МЛТ-0,25-6,8 кОм
R2 С1-4-0,25-910 Ом
...........
Диоды
VD1 Д9А
.........
Транзисторы
VT1 КТ315А
............
|
0,5
.....
0,06
0,05
.....
0,043
0,04
.....
02
.....
05
.....
|
50
.....
40
40
.....
40
45
.....
50
.....
50
.....
|
0,3
.....
06
05
.....
0,1
0,2
.....
0,3
.....
0,5
.....
|
0,7
.....
0,45
0,4
.....
0,3
0,5
.....
0,8
.....
0,6
.....
|
0,35
.....
0,027
0,020
.....
0,013
0,020
.....
0,16
.....
0,30
.....
|
| Итого интенсивность отказов устройства
| |
Таблица 2.4
Поправочные коэффициенты  ,
,  и
и  в зависимости от воздействия механических факторов на неамортизированную аппаратуру
в зависимости от воздействия механических факторов на неамортизированную аппаратуру
| Условия эксплуатации
аппаратуры
| Вибрации

| Ударные нагрузки

| Суммарное воздействие  и и 

|
| Лабораторные
Стационарные (полевые)
Корабельные
Автофургонные
Железнодорожные
Самолётные
| 1,00
1,04
1,30
1,35
1,40
1,46
| 1,00
1,03
1,05
1,08
1,10
1,13
| 1,00
1,07
1,37
1,46
1,54
1,65
|
Таблица 2.5
Поправочный коэффициент  на влажность
на влажность
| Влажность, %
| Температура, 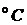
| Коэффициент, 
|
| 60 ÷ 70
90 ÷ 98
90 ÷ 98
| 20 ÷ 40
20 ÷ 25
30 ÷ 40
| 1,0
2,0
2,5
|
Интенсивность отказов элемента  при эксплуатации в реальных условиях равна номинальной интенсивности отказов
при эксплуатации в реальных условиях равна номинальной интенсивности отказов  , умноженной на поправочные коэффициенты
, умноженной на поправочные коэффициенты  .
.
При расчётах бывает полезно знать интервал времени, в пределах которого будет находиться вероятность безотказной работы изделия с выбранной доверительной вероятностью. В этом случае интенсивности отказов следует дополнительно умножать на величину относительного времени работы.
Таблица 2.6
Поправочный коэффициент  на давление
на давление
| Высота, км
| Коэффициент, 
|
| Высота, км
| Коэффициент, 
|
| 0 ÷ 1
1 ÷ 2
2 ÷ 3
3 ÷ 5
5 ÷ 6
6 ÷ 8
| 1,00
1,05
1,10
1,14
1,16
1,20
| 8 ÷ 10
10 ÷ 15
15 ÷ 20
20 ÷ 25
25 ÷ 30
30 ÷ 40
| 1,25
1,30
1,35
1,38
1,40
1,45
|
Лекция 3. «Основные понятия теории случайных процессов»
План лекции:
Основные понятия теории случайных процессов
Связь интенсивности отказов с плотностью распределения вероятностей
Основные понятия теории случайных процессов
Для количественной оценки показателей надёжности необходимо иметь статистический материал, который может быть получен в результате проведения испытаний.
В теории вероятностей испытанием, опытом или экспериментом называют некоторую воспроизводимую совокупность условий, в которых наблюдается то или другое явление, фиксируется тот или иной результат. Если результат может быть различным при повторении опыта, то такой случай называют опытом со случайным исходом.
Так как моменты появления отказов носят случайный характер, то для оценки основных показателей надёжности используют математический аппарат теории вероятностей. Поэтому при оценке надёжности изделий объектами исследований являются случайные величины и случайные события.
Случайной называют такую величину, которая в результате опыта может принимать то или иное, заранее неизвестное (случайное) значение.
Случайные величины могут быть дискретными и непрерывными. Например, время работы изделия до отказа или время ремонта являются непрерывными случайными величинами.
Случайным событием называют всякий факт, который в опыте со случайным исходом может произойти или не произойти. Например, отказы представляют собой случайные события.
Случайные события, происходящие во времени и образующие некоторую последовательность, называют потоком событий.
Процесс – последовательная смена состояний системы.
Случайным называют процесс, состояние которого при любом фиксированном моменте времени, является случайной величиной. Переход изделия из одного состояния в другое (например, из работоспособного в неработоспособное и обратно) является случайным процессом.
Совокупность вероятностей всех значений, которые может принимать случайная величина, называют распределением вероятностей.
Закономерности, наблюдаемые в распределении вероятностей случайных величин, называют законами распределения случайных величин. Таким образом, законом распределения случайной величины называют всякое соотношение, устанавливающее связь между возможными значениями случайной величины 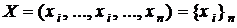 и соответствующими вероятностями
и соответствующими вероятностями  её появления. Закон распределения
её появления. Закон распределения  может быть задан формулой, таблицей, графиком и другими способами.
может быть задан формулой, таблицей, графиком и другими способами.
Непрерывные и дискретные случайные величины  характеризуют вероятностью того, что они меньше некоторого значения текущей переменной величины
характеризуют вероятностью того, что они меньше некоторого значения текущей переменной величины  . Эту характеристику называют интегральным законом распределения или функцией распределения
. Эту характеристику называют интегральным законом распределения или функцией распределения  случайной величины X:
случайной величины X:

Функция распределения 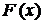 любой случайной величины
любой случайной величины  есть неубывающая функция своего аргумента, то есть
есть неубывающая функция своего аргумента, то есть  , если
, если  .
.
Значения функции распределения  заключены в интервале от 0 до 1:
заключены в интервале от 0 до 1:  , причём
, причём  , а
, а  .
.
Функция распределения непрерывной случайной величины является также непрерывной. Функция распределения дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений.
Производную от функции распределения непрерывной случайной величины

называют плотностью распределения или дифференциальным законом распределения. График плотности распределения 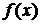 называют кривой распределения. Обратный переход от плотности распределения к функции распределения осуществляют по формуле
называют кривой распределения. Обратный переход от плотности распределения к функции распределения осуществляют по формуле

Плотность распределения 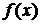 есть неотрицательная функция, т.е. вся кривая распределения лежит не ниже оси абсцисс. Интеграл в бесконечных пределах от плотности распределения
есть неотрицательная функция, т.е. вся кривая распределения лежит не ниже оси абсцисс. Интеграл в бесконечных пределах от плотности распределения 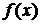 равен единице.
равен единице.
В теории надёжности наибольшее распространение получили:
– биномиальный закон и распределение Пуассона – для дискретных случайных величин и
– экспоненциальный закон, закон Вейбулла, нормальный и логарифмически нормальный законы – для непрерывных случайных величин.
Каждый закон распределения исчерпывающим образом описывает распределение вероятностей и даёт возможность вычислять вероятности любых событий, связанных со случайной величиной. Однако во многих практических случаях бывает достаточно знать только некоторые отдельные количественные параметры, характеризующие основные характеристики распределения. Эти числа, выражающие в сжатой форме наиболее существенные черты распределения, называют числовыми характеристиками случайной величины.
Среди числовых характеристик случайных величин различают характеристики положения, фиксирующие положение случайной величины на числовой оси, и моменты, характеризующие особенности её распределения.
Математическим ожиданием  или средним значением (более точно средним взвешенным значением) случайной величины
или средним значением (более точно средним взвешенным значением) случайной величины  называют:
называют:
a) для дискретной величины – сумму произведений всех возможных её значений на вероятности этих значений:

б) для непрерывной величины – интеграл в бесконечных пределах от произведения значений случайной величины на плотность распределения:

Математическое ожидание характеризует положение центра распределения случайной величины.
Другой характеристикой положения случайной величины является мода  – наиболее вероятное значение случайной величины.
– наиболее вероятное значение случайной величины.
Для описания непрерывной случайной величины иногда применяют ещё одну характеристику положения – медиану  – такое значение
– такое значение  случайной величины X, для которого выполняется условие
случайной величины X, для которого выполняется условие

то есть медиана – абсцисса точки, для которой площади кривой распределения, лежащие слева и справа от неё, одинаковы и равны 0,5.
Начальным моментом  -го порядка
-го порядка  случайной величины X называют математическое ожидание
случайной величины X называют математическое ожидание  -й степени этой величины.
-й степени этой величины.
Отсюда следует, что среднее значение случайной величины есть её первый начальный момент.
Центрированной случайной величиной  называют отклонение случайной величины от её математического ожидания:
называют отклонение случайной величины от её математического ожидания:

Поэтому среднее значение центрированной случайной величины равно нулю.
Моменты центрированной случайной величины называют центральными моментами.
Наиболее часто используют второй центральный момент, называемый дисперсией:

Иногда бывает удобнее вычислять дисперсию по другой формуле, получающейся из (3.8) после раскрытия круглых скобок,


Дисперсия характеризует рассеивание случайной величины и представляет собой среднее значение квадрата отклонения случайной величины от её среднего значения. Дисперсия имеет размерность квадрата случайной величины, что не очень удобно. Поэтому в качестве ещё одной числовой характеристики случайной величины используют среднеквадратическое отклонение.
Среднеквадратическим отклонением  или стандартом случайной величины X называют квадратный корень из дисперсии
или стандартом случайной величины X называют квадратный корень из дисперсии

имеющий размерность случайной величины.
Для неотрицательной случайной величины X иногда применяют коэффициент вариации, равный отношению среднеквадратического отклонения к математическому ожиданию

характеризующий рассеивание случайной величины в относительных единицах и измеряемый обычно в процентах.
Коэффициент вариации показывает, какую долю математического ожидания составляет среднеквадратическое отклонение и характеризует "степень случайности" неотрицательной случайной величины.
Моменты выше второго порядка служат для более подробного описания распределения. Например, третий центральный момент  характеризует асимметрию распределения. Однако удобнее использовать безразмерную величину – коэффициент асимметрии (коэффициент "скошенности" от английского skew – "косой"):
характеризует асимметрию распределения. Однако удобнее использовать безразмерную величину – коэффициент асимметрии (коэффициент "скошенности" от английского skew – "косой"):

Четвёртый центральный момент  характеризует плоскостность распределения случайной величины с помощью коэффициента, называемого эксцессом:
характеризует плоскостность распределения случайной величины с помощью коэффициента, называемого эксцессом:

Четвёртый центральный момент применяют в основном к непрерывным случайным величинам. В качестве опорного используют нормальное распределение случайной величины, для которого  . В этом случае более островершинные распределения будут иметь положительный эксцесс, более плосковершинные – отрицательный.
. В этом случае более островершинные распределения будут иметь положительный эксцесс, более плосковершинные – отрицательный.



 ,
отк / час
,
отк / час
 ,
,



 отк / час
отк / час
 ,
,  и
и  в зависимости от воздействия механических факторов на неамортизированную аппаратуру
в зависимости от воздействия механических факторов на неамортизированную аппаратуру на влажность
на влажность при эксплуатации в реальных условиях равна номинальной интенсивности отказов
при эксплуатации в реальных условиях равна номинальной интенсивности отказов  , умноженной на поправочные коэффициенты
, умноженной на поправочные коэффициенты  .
. на давление
на давление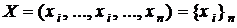 и соответствующими вероятностями
и соответствующими вероятностями  её появления. Закон распределения
её появления. Закон распределения  может быть задан формулой, таблицей, графиком и другими способами.
может быть задан формулой, таблицей, графиком и другими способами. . Эту характеристику называют интегральным законом распределения или функцией распределения
. Эту характеристику называют интегральным законом распределения или функцией распределения  случайной величины X:
случайной величины X:
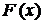 любой случайной величины
любой случайной величины  , если
, если  .
. , причём
, причём  , а
, а  .
.
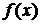 называют кривой распределения. Обратный переход от плотности распределения к функции распределения осуществляют по формуле
называют кривой распределения. Обратный переход от плотности распределения к функции распределения осуществляют по формуле
 или средним значением (более точно средним взвешенным значением) случайной величины
или средним значением (более точно средним взвешенным значением) случайной величины 

 – наиболее вероятное значение случайной величины.
– наиболее вероятное значение случайной величины. – такое значение
– такое значение  случайной величины X, для которого выполняется условие
случайной величины X, для которого выполняется условие
 -го порядка
-го порядка  случайной величины X называют математическое ожидание
случайной величины X называют математическое ожидание 



 или стандартом случайной величины X называют квадратный корень из дисперсии
или стандартом случайной величины X называют квадратный корень из дисперсии

 характеризует асимметрию распределения. Однако удобнее использовать безразмерную величину – коэффициент асимметрии (коэффициент "скошенности" от английского skew – "косой"):
характеризует асимметрию распределения. Однако удобнее использовать безразмерную величину – коэффициент асимметрии (коэффициент "скошенности" от английского skew – "косой"):
 характеризует плоскостность распределения случайной величины с помощью коэффициента, называемого эксцессом:
характеризует плоскостность распределения случайной величины с помощью коэффициента, называемого эксцессом:
 . В этом случае более островершинные распределения будут иметь положительный эксцесс, более плосковершинные – отрицательный.
. В этом случае более островершинные распределения будут иметь положительный эксцесс, более плосковершинные – отрицательный.


