

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
С ростом значения параметра  эта функция сходится к гауссовской плотности вероятности с математическим ожиданием
эта функция сходится к гауссовской плотности вероятности с математическим ожиданием  и дисперсией
и дисперсией  .При
.При  распределение переходит в распределение Релея.
распределение переходит в распределение Релея.
Пример:
pd = makedist(‘rician’, ‘s’, 4, ‘  ’, 2);
’, 2);
y=random(pd, 10000, 1); % Выборкаобъема n=10000;
x=0:0.01:15;
 ;
;
plot(x,w)
2.5. Формирование вещественного массива выборочных значений случайной величины, имеющей распределение Релея
Синтаксис:
pd = makedist(‘Rayleigh’, ‘b’, 2);
y=random(pd, n, 1);
Описание:
Функция MATLAB pd = makedist(‘Rayleigh’, ‘  ’, 2) создает скрипт-файлраспределения Релея с параметром масштаба
’, 2) создает скрипт-файлраспределения Релея с параметром масштаба  .
.
Функция MATLAB y=random(pd, n, 1) генерирует массив y размера  , элементами которого являются выборочные значения случайной величины, имеющей плотность вероятности pd.
, элементами которого являются выборочные значения случайной величины, имеющей плотность вероятности pd.
Аналитическое выражение для соответствующей плотности вероятности имеет вид:
 ,
,  .
.

Рис.6. Плотность вероятности распределения Релея
График этой плотности, представлен на рис.6 для  .
.
График построен с помощью функции MATLAB  , где
, где  – массив значений аргумента плотности вероятности, для которого вычисляются значения
– массив значений аргумента плотности вероятности, для которого вычисляются значения  плотности
плотности  .
.
Пример:
pd = makedist(‘Rayleigh’, ‘  ’, 2);
’, 2);
y=random(pd, 10000, 1); % Выборкаобъемаn=10000;
x=0:0.01:15;
 ;
;
plot(x,w)
2.6. Формирование вещественного массива выборочных значений случайной величины, имеющей логарифмически нормальное распределение
Синтаксис:
pd = makedist(‘Lognormal’, ‘mu’, 2, ‘  , 1); w=
, 1); w=
y=random(pd, n, 1);
Функция y=random(pd, n,1) формирует выборку y размера  , элементами которой являются выборочные значениями случайной величины, имеющей логарифмически нормальное (логнормальное) распределение.
, элементами которой являются выборочные значениями случайной величины, имеющей логарифмически нормальное (логнормальное) распределение.

Рис. 7. Плотность вероятности логарифмически нормального распределения
Функция MATLAB pd = makedist(‘Lognormal’, ‘mu’, 2, ‘  ’, 1) создает скрипт-файл логарифмически нормального распределения с параметром нецентральностиmu
’, 1) создает скрипт-файл логарифмически нормального распределения с параметром нецентральностиmu  и масштаба
и масштаба  .
.
|
|
Аналитическое выражение для соответствующей плотности вероятности имеет вид:
 ,
,  .
.
График этой плотности для mu  и
и  приведен на рис.7.График построен с помощью функции MATLABw
приведен на рис.7.График построен с помощью функции MATLABw  , где
, где  – массив значений аргумента плотности вероятности, для которого вычисляются значения w плотности
– массив значений аргумента плотности вероятности, для которого вычисляются значения w плотности  .
.
Пример:
pd = makedist(‘Lognormal’,’mu’,2, ‘  ’, 2);
’, 2);
y=random(pd, 10000, 1); % Выборкаобъема n=10000;
x=0:0.01:70;
 ;
;
plot(x,w)
2.7. Формирование вещественного массива выборочных значений случайной величины, имеющей полигауссовское распределение
Синтаксис:
 ;
;
 ;
;
Описание:
mu – матрица размера  , определяющая математические ожидания
, определяющая математические ожидания  гауссовских случайных величин, являющихся компонентами смеси;
гауссовских случайных величин, являющихся компонентами смеси;
 – определяет ковариации каждой компонентысмеси; размер матрицы
– определяет ковариации каждой компонентысмеси; размер матрицы  в данной работеравен
в данной работеравен  ;
;
 – вектор размера
– вектор размера  , определяющий вероятности появления выборочных значений гауссовских компонент.
, определяющий вероятности появления выборочных значений гауссовских компонент.
Функция  формирует матрицуразмера
формирует матрицуразмера  выборочных значений случайной величины с плотностьювероятности obj.
выборочных значений случайной величины с плотностьювероятности obj.
Полигауссовская плотность вероятности может быть задана аналитически следующим выражением:
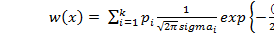 ,
,  .
.
На рис.8 представлен график полигауссовской плотности для следующих численных значений параметров:
 .
.

Рис.8. Плотность полигауссовского распределения
График построен с помощью функции MATLAB  . Здесь
. Здесь  – массив значений плотности вероятности obj для значений [-1:0.01:7]аргумента
– массив значений плотности вероятности obj для значений [-1:0.01:7]аргумента  .
.
Пример:
obj= gmdistribution([2 5]’, 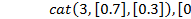 ;
;
y=random(obj, 10000); % Выборкаобъемаn=10000;
x=0:0.01:7;
 ;
;
plot(x,w)
3.8. Приложение 2. Выбор вариантов
Таблица 1
| № вар. | Распределение | Значения параметров плотности вероятности |
| 1. | Хи-квадрат | 1.1:  1.2:
1.2:  1.3:
1.3:  1.4:
1.4: 
|
| 2. | Релея | 2.5:  2.6:
2.6:  2.7:
2.7:  2.8:
2.8: 
|
| 3. | Райса | 3.9: s  ;
3.10: ;
3.10:  ;
3.11: ;
3.11:  ;
3.12: ;
3.12:  ; ;
|
| 4. | Логнормальное | 4.13:  ;
4.14: ;
4.14:  ;
4.15: ;
4.15:  ;
4.16: ;
4.16:  ; ;
|
| Полигауссовское | 5.17:  5.18:
5.18:  5.19:
5.19:  5.20:
5.20:  5.21:
5.21: 
| |
Номер варианта работы, выполняемого студентом, определяется номером его фамилии в журнале группы, который определяет второе число во втором столбце табл. 1.
|
|
3.9. Приложение 3. Пример исследования 1
В данном разделе приведен пример исследования случайной выборки, полученной с помощью датчика случайных чисел с нормальным распределением с нулевым математическим ожиданием ( ) и дисперсией, равной 1 (
) и дисперсией, равной 1 ( ).
).
В соответствии с изложенным в Приложении 1 в системе MATLAB генератор квазислучайных чисел с таким распределением и значениями параметров его плотности вероятности оформлен как m-функция. Обращение к такому генератору в строке командного окна MATLAB должно быть записано следующим образом:
y=randn(n, 1);
n – размер формируемой выборки. В результате выполнения этой команды в массив y (вектор-столбец) рабочего пространства будет помещена выборка, сформированная этим датчиком.
Ниже приведены все команды системы MATLAB, необходимые для вычисления и построения гистограммы выборки и графика теоретической плотности вероятности гауссовской случайной величины.
% Построение и аппроксимация гистограммы выборки %
randn('seed',0); % Устанавливает датчик псевдослучайных чисел в исходное состояние; %
normal=randn(10000,1); % Датчик randn формирует матрицу размера 10000х1, элементами которой являются выборочные значения случайной величины, имеющей нормальное распределение с математическим ожиданием 0 и дисперсией 1; матрица помещена в массив с именем normal рабочего пространства%
m=mean(normal); % Вычисление значения начального выборочного момента первого порядка - среднеарифметического значения выборки (оценка математического ожидания случайной величины;%
sigma=std(normal); % Вычисление значения второго центрального выборочного момента - среднеквадратического отклонения случайной величины от математического ожидания;%
[N,X]=hist(normal,25); % Выборка normal обрабатывается функцией MATLAB hist (вычисление ненормированной гистограммы), для которой выбрано число подинтервалов  . Здесь N - вектор, i -тая компонента которого равна числу элементов выборки, попавших в i -тыйподинтервал; Х - вектор, i -тая компонента которого определяет положение на оси абсцисс центра i -го подинтервала; %
. Здесь N - вектор, i -тая компонента которого равна числу элементов выборки, попавших в i -тыйподинтервал; Х - вектор, i -тая компонента которого определяет положение на оси абсцисс центра i -го подинтервала; %
bar(X, N/(10000*(X(2)-X(1))),’g-‘) % Вычисление значений и построение гистограммы выборки; %
hold; % Данная команда устанавливает режим сохранения текущего графического окна, что позволяет в этом окне построить последовательно несколько графиков;%
|
|
plot(X, exp(-(X-m).^2/(2*sigma^2))/((sqrt(2*pi)*sigma)),'r-') % Вычисление значений и построение графика функции плотности вероятности %;
title(‘Гистограмма выборки из гауссовского распределения’); % Заголовок рисунка %
xlabel(‘Значения случайной величины’);
ylabel(‘Значения плотности вероятности');
grid; % Нанесение координатной сетки; %

Рис. 8. Гистограмма выборки стандартной гауссовской случайной величины
На рис. 8 представлены графики, полученные в результате выполнения приведенных выше команд системы MATLAB.
3.10. Приложение 4. Пример исследования 2
В данном разделе приведен пример статистической обработки случайной выборки, полученной с помощью датчика случайных чисел с нормальным распределением с математическим ожиданием  и среднеквадратическим отклонением sigma.
и среднеквадратическим отклонением sigma.
В системе MATLAB генератор квазислучайных чисел с таким распределением и заданными значениями параметров его плотности вероятности оформлен как m-функция. Обращение к такому генератору в строке командного окна MATLAB должно быть записано следующим образом:
y=normrnd(a, sigma, n, 1);
где n – размер формируемой выборки. В результате выполнения этой команды в массив y (вектор-столбец) рабочего пространства системы MATLAB будет помещена выборка, сформированная этим датчиком.
Ниже приведены все команды системы MATLAB, необходимые для вычисления и построения эмпирической функции распределения и графика теоретической функции распределения рассматриваемой здесь гауссовской случайной величины.
%Построение и аппроксимация эмпирической функции распределения%
norma=normrnd(10, 1, 50,1); % Датчик normrnd формирует матрицу размера 50х1, элементами которой являются выборочные значения случайной величины, имеющей нормальное распределение с математическим ожиданием 10 и среднеквадратическим отклонением 1; матрица помещена в массив с именем norma рабочего пространства MATLAB %
cdfplot(norma) % Вычисление и построение графика эмпирической функции распределения  по выборке norma %
по выборке norma %
hold on
x=2:0.1:20;
F=normcdf(x, 10, 1);
plot(x,F,’r-‘)

Рис. 9. Построение и аппроксимация эмпирической функции распределения
Приложение5. Некоторые функции MATAB, полезные при исследовании распределений случайных величин
|
|
1. Вычисление значений функции распределения при известной плотности вероятности:
pd=makedist(‘Normal’);
x=-3:.1:3;
cdf_normal=cdf(pd, x);
2. Вычисление и построение гистограммы выборки с последующей аппроксимацией теоретической кривой:
y=normrnd(10,2,1000,1);
figure(2)
histfit(y)
3. Вычисление и построение гистограммы выборки с заданным числом столбцов и сглаживание ее заданной плотностью вероятности:
b=betarnd(3,10,1000,1);
figure(3)
histfit(b,15,’beta’)
4. Графический интерфейс для исследования влияния изменения значений параметров на форму плотности вероятности и функции распределения:
disttool

Рис.10.
Можно выбрать вид распределения, тип функции и установить различные значения параметров этого распределения, после ввода которых автоматически строится график плотности или функции распределения.
|
|
|

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!