Теорема. Если функция 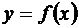 в некоторой точке x = x 0 имеет (конечную) производную
в некоторой точке x = x 0 имеет (конечную) производную 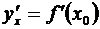 , то
, то
1) приращение функции может быть представлено в виде
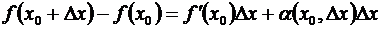 , (3.6)
, (3.6)
или, короче, 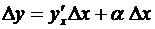 , где a есть величина, зависящая от D x и вместе с ним стремящаяся к нулю, т.е.
, где a есть величина, зависящая от D x и вместе с ним стремящаяся к нулю, т.е. 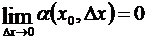 ;
;
2) функция в этой точке необходимо непрерывна.
Доказательство. 1) Согласно определению производной, 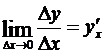 . Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем
. Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем
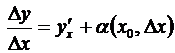 , где
, где 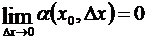 .
.
Определяя отсюда D y, придем к формуле (3.6).
2) Чтобы доказать непрерывность функции, рассмотрим выражение (3.6). При D x ®0 сумма в правой части (3.6) обращается в нуль. Следовательно, 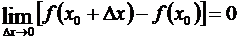 , или
, или 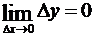 , а это означает, что функция в точке x 0 непрерывна.
, а это означает, что функция в точке x 0 непрерывна.
Из доказанной теоремы следует, что функция, имеющая производную в данной точке, будет непрерывной в этой точке. Однако непрерывная в данной точке функция не всегда имеет производную в этой точке. Так, в точке x 0 = 1 функция y = | x – 1| является непрерывной, но производной в этой точке не имеет. Это означает, что данное условие является лишь необходимым.
Производная сложной функции
Теорема. Пусть 1) функция v = j (x) имеет в некоторой точке x производную 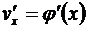 , 2) функция y = f (v) имеет в соответствующей точке v производную
, 2) функция y = f (v) имеет в соответствующей точке v производную 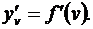 Тогда сложная функция у = f (j (x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f (v) и j (x): [ f (j (x)) ] ' =
Тогда сложная функция у = f (j (x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f (v) и j (x): [ f (j (x)) ] ' = 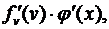 или короче
или короче
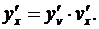 (3.7)
(3.7)
Доказательство. Придадим х произвольное приращение Δ х; пусть Δ v – соответствующее приращение функции v = j (x) и, наконец, Δ у – приращение функции y = f (v), вызванное приращением Δ v. Воспользуемся соотношением (3.6), которое, заменяя x на v, перепишем в виде 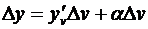 (a зависит от Δ v и вместе с ним стремится к нулю). Разделив его почленно на D x, получим
(a зависит от Δ v и вместе с ним стремится к нулю). Разделив его почленно на D x, получим
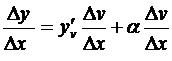 .
.
Если D x устремить к нулю, то, согласно (3.6) (при условии, что у = v), будет стремиться к нулю и Δ v, а тогда, как мы знаем, будет также стремиться к нулю зависящая от Δ v величина a. Следовательно, существует предел
 ,
,
который и представляет собой искомую производную 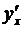 .
.
Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила (3.7). Так, если у = f (u), u = j (v), v = y (x), то
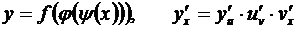 . (3.8)
. (3.8)
Примеры. 1. Пусть y = log a sin x,иначе говоря, y = log a v, где v = sin x. По правилу (3.7)
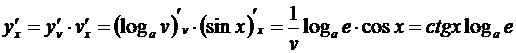 .
.
2.  , т.е. y = eu, u = v 2, v = sin x. По правилу (3.8)
, т.е. y = eu, u = v 2, v = sin x. По правилу (3.8)
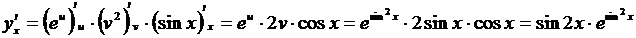 .
.
1.7. Производная показательно – степенной функции
Пусть u = u (x) > 0 и v = v (x) – функции, имеющие производные в фиксированной точке x. Найдем производную функции y = uv. Логарифмируя это равенство, получим: ln y = v ln u.
Продифференцируем обе части данного равенства по x:
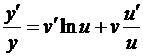 .
.
Отсюда 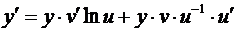 , или
, или
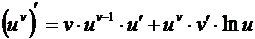 . (3.9)
. (3.9)
Таким образом, производная показательно – степенной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х, а v есть постоянная (т.е. рассматривать uv как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u = const (т.е. рассматривать uv как показательную функцию).
Примеры. 1. Если y = xtg x, то, полагая u = x, v = tg x,согласно (3.9) имеем
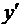 = tg x xtg x – 1 + xtg x ln x sec2 x.
= tg x xtg x – 1 + xtg x ln x sec2 x.
Прием, примененный в данном случае для нахождения производной и состоящий в том, что сначала находят производную логарифма рассматриваемой функции, широко применяется при дифференцировании функций: при отыскании производной функции эти функции сначала логарифмируют, а затем из равенства, полученного после дифференцирования логарифма функции, определяют производную функции. Такая операция называется логарифмическим дифференцированием.
2.Требуется найти производную от функции
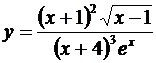 .
.
Логарифмируя, находим:
ln y = 2ln(x + 1) + 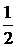 ln(x – 1) – 3 ln(x + 4) – x.
ln(x – 1) – 3 ln(x + 4) – x.
Дифференцируем обе части последнего равенства:
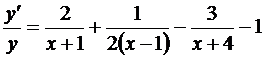 .
.
Умножая на у и подставляя 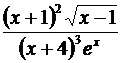 вместо у, получаем:
вместо у, получаем:
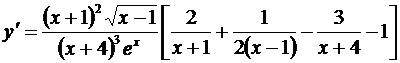 .
.



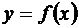 в некоторой точке x = x 0 имеет (конечную) производную
в некоторой точке x = x 0 имеет (конечную) производную 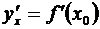 , то
, то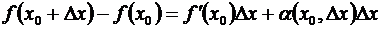 , (3.6)
, (3.6)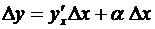 , где a есть величина, зависящая от D x и вместе с ним стремящаяся к нулю, т.е.
, где a есть величина, зависящая от D x и вместе с ним стремящаяся к нулю, т.е. 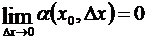 ;
;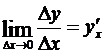 . Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем
. Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем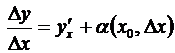 , где
, где 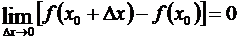 , или
, или 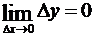 , а это означает, что функция в точке x 0 непрерывна.
, а это означает, что функция в точке x 0 непрерывна.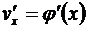 , 2) функция y = f (v) имеет в соответствующей точке v производную
, 2) функция y = f (v) имеет в соответствующей точке v производную 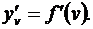 Тогда сложная функция у = f (j (x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f (v) и j (x): [ f (j (x)) ] ' =
Тогда сложная функция у = f (j (x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f (v) и j (x): [ f (j (x)) ] ' = 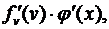 или короче
или короче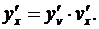 (3.7)
(3.7)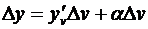 (a зависит от Δ v и вместе с ним стремится к нулю). Разделив его почленно на D x, получим
(a зависит от Δ v и вместе с ним стремится к нулю). Разделив его почленно на D x, получим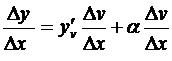 .
. ,
,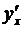 .
.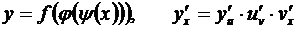 . (3.8)
. (3.8)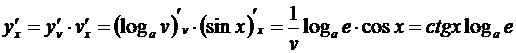 .
. , т.е. y = eu, u = v 2, v = sin x. По правилу (3.8)
, т.е. y = eu, u = v 2, v = sin x. По правилу (3.8)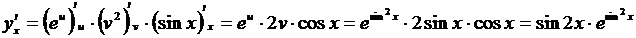 .
.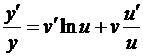 .
.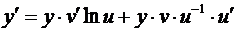 , или
, или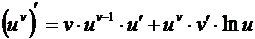 . (3.9)
. (3.9)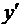 = tg x xtg x – 1 + xtg x ln x sec2 x.
= tg x xtg x – 1 + xtg x ln x sec2 x.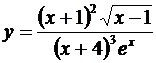 .
.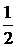 ln(x – 1) – 3 ln(x + 4) – x.
ln(x – 1) – 3 ln(x + 4) – x.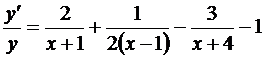 .
.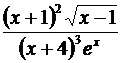 вместо у, получаем:
вместо у, получаем: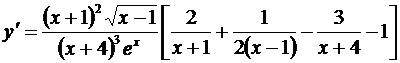 .
.


