

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Перепишем формулу (3.13), заменив в ней главную часть приращения функции дифференциалом
 . (3.21)
. (3.21)
Из полученного выражения следует, что хотя дифференциал dy функции  не равен приращению D y этой функции, но, так как
не равен приращению D y этой функции, но, так как  , то с точностью до бесконечно малой более высокого порядка, чем D х, справедливо приближенное равенство
, то с точностью до бесконечно малой более высокого порядка, чем D х, справедливо приближенное равенство
D y» dy. (3.22)
Относительная погрешность этого равенства становится сколь угодно малой при достаточно малом D х.
Выгода замены приращения функции D у ее дифференциалом dy состоит в том, что dy зависит от D х линейно, в то время как D у представляет собой обыкновенно более сложную функцию от D х.
Если положить D х = х – х 0 и х 0 + D х = х, то равенство (3.22) принимает вид: f (x) – f (x 0) » 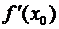 (x – x 0) или
(x – x 0) или
f (x) = f (x 0) + 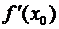 (x – x 0). (3.23)
(x – x 0). (3.23)
Формула (3.23) определяет способ приближенного вычисления функции. По этой формуле для значений х, близких к х 0, функция f (x) приближенно заменяется линейной функцией. Геометрически это соответствует замене участка кривой y = f (x), примыкающего к точке (х 0, f (x 0)), отрезком касательной к кривой в этой точке (см. формулу (3.3)).
В частности, взяв для простоты х 0 = 0 и ограничиваясь малыми значениями х, будем иметь приближенную формулу:
f (x) » f (0) +  x. (3.24)
x. (3.24)
Отсюда, подставляя вместо f (x) различные элементарные функции, легко получить ряд приближенных формул:
(1+ x) m = 1+ mx; sin x» x; tg x» x; ex» 1+ x; ln(1+ x) » x и т.п.
§3. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
ЧИСЛОВОЙ ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
3.1. Определение производной n -го порядка
Как уже отмечалось в §1, п.1.1, производная  функции y = f (x), определенной и дифференцируемой на некотором промежутке Р представляет собой функцию, также определенную на промежутке Р. Может случиться, что эта функция
функции y = f (x), определенной и дифференцируемой на некотором промежутке Р представляет собой функцию, также определенную на промежутке Р. Может случиться, что эта функция  сама является дифференцируемой в некоторой точке х промежутка Р, т.е. имеет в этой точке производную. Тогда указанную производную называют второй производной (или производной второго порядка) функции у = f (x) в упомянутой точке х, и обозначают одним из символов
сама является дифференцируемой в некоторой точке х промежутка Р, т.е. имеет в этой точке производную. Тогда указанную производную называют второй производной (или производной второго порядка) функции у = f (x) в упомянутой точке х, и обозначают одним из символов
|
|

После того как введено понятие второй производной, можно последовательно ввести понятие третьей производной, затем четвертой производной и т.д. Если предположить, что нами уже введено понятие (n – 1)-й производной и что (n – 1)-я производная дифференцируемая в некоторой точке х промежутка Р, т.е. имеет в этой точке производную, то указанную производную называют n - й производной (или производной n-го порядка) функции у = f (x) в точке х и для обозначения ее применяются символы:

Соотношение, определяющее n- ю производную, имеет вид
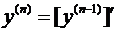 . (3.25)
. (3.25)
Функцию, имеющую на данном промежутке Р конечную производную порядка n, обычно называют n раз дифференцируемой на данном промежутке.
3.2. Вычисление производной n-го порядка
Методика вычисления производных высшего порядка предполагает умение вычислять только производные первого порядка. Поэтому для того чтобы вычислить n- ю производную от какой-либо функции, нужно предварительно вычислить производные всех предшествующих порядков. В качестве примеров вычислим производные n- го порядка некоторых элементарных функций.
1) Рассмотрим сначала степенную функцию  (х > 0, μ Î R). Последовательно дифференцируя, будем иметь
(х > 0, μ Î R). Последовательно дифференцируя, будем иметь
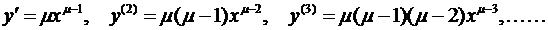
Отсюда легко уяснить общий закон
 .
.
Если, например, взять μ = –1, то получим
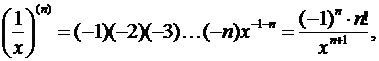
а при 
 и т.п.
и т.п.
2) Пусть теперь  Прежде всего имеем
Прежде всего имеем 
Возьмем отсюда производную (n – 1)-го порядка по соответствующей формуле из 1), заменив в ней n на n – 1; мы и получим тогда
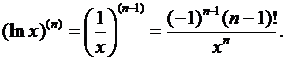
3) Если у = ах (0 < а ¹ 1), то 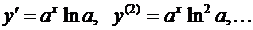 .
.
Общая формула, легко устанавливая по методу индукции, имеет вид

4) Положим 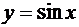 ; тогда
; тогда 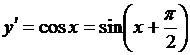 . Таким образом, дифференцирование функции
. Таким образом, дифференцирование функции 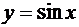 прибавляет к аргументу этой функции величину.
прибавляет к аргументу этой функции величину.  Отсюда получаем формулу
Отсюда получаем формулу 
|
|
5) Аналогично устанавливается и формула 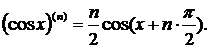
3.3. Формула Лейбница для n -й производной произведения двух функций
В то время как установленное в §1, п.1.4 правило вычисления первой производной от суммы или разности двух функций 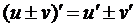 легко переносится (например, последовательным применением этих правил) на случай n -й производной (u ± v)(n) = u (n) ± v (n), возникают большие затруднения при вычислении n -й производной от произведения двух функций
легко переносится (например, последовательным применением этих правил) на случай n -й производной (u ± v)(n) = u (n) ± v (n), возникают большие затруднения при вычислении n -й производной от произведения двух функций  .
.
Соответствующее правило носит название формулы Лейбница, и имеет следующий вид:

 (3.26)
(3.26)
Примеры. Вычислить n -ю производную функций:
1. у = х 2cos x. Воспользуемся формулой Лейбница, положив в ней  В таком случае для любого номера к
В таком случае для любого номера к 
 Следовательно,
Следовательно,

2.  Положим
Положим  Тогда
Тогда 


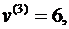
 Таким образом,
Таким образом,

Рассмотренные примеры показывают, что формула Лейбница особенно эффективна в случае, когда одна из двух перемножаемых функций имеет лишь конечное число отличных от нуля производных.
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!