Пусть нам дана конечная, однородная струна, закреплённая на концах (т.е. в точках x= 0 и x=l). Если на неё не действуют внешние силы, то функция u (x,t), дающая закон колебания струны должна удовлетворять уравнению:
 .
.
Граничным условиям:
u (0, t)=0; u (l,t)=0.
И начальным условиям:

 .
.
Здесь сформулирована 1-я краевая задача. Видно, что как само уравнение, так и дополнительные условия (граничные) однородны, поэтому если некоторые функции удовлетворяют уравнению и граничным условиям, то и любая их линейная комбинация также удовлетворяет этому уравнению и граничным условиям. На этом и основан метод Фурье. Суть его заключается в том, что на первом этапе мы находим некоторый запас функций, удовлетворяющих уравнению и граничным условиям; пусть это будут функции u 1(x,t), u 2(x,t), …, un (x,t) … На втором этапе строится линейная комбинация из этих функций:
u (x,t) =c 1 u 1(x,t) + c 2 u 2(x,t) +…+ cnun (x,t) +…
Здесь под линейной комбинацией понимается и сумма бесконечного ряда.
В силу однородности уравнения и однородности граничных условий эта сумма также удовлетворяет и уравнению и граничным условиям при любых значениях коэффициентов ряда ci; остаётся подобрать эти коэффициенты так, чтобы функция u (x,t) удовлетворяла и начальным условиям.
Для того чтобы осуществить этот план, попытаемся найти такие решения, которые представимы в виде произведения двух функций, одна из которых зависит только от x (обозначим её X (x)), другая только от t (обозначим её T (t)):
u (x,t) = X (x)× T (t).
Если эта функция удовлетворяет уравнению колебаний, то в результате её подстановки в уравнение колебаний получим тождество:
 .
.
Проведём дифференцирование:
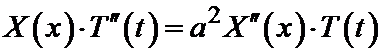 .
.
Разделим переменные в этом тождестве, т.е. всё, что зависит от x переносим в одну сторону, всё что от t – в другую, получим:

Выражения, стоящие в обеих частях не зависят ни от x, ни от t. Действительно, левая часть не зависит от x, значит и правая от x не зависит. Далее, правая часть не зависит от t; следовательно, не зависит от t и левая часть. Значит обе части равенства вообще не зависят ни от x ни от t – следовательно, они константы:

Отсюда получаем два уравнения:

 .
.
Поскольку мы ищем частные решения, удовлетворяющие граничным условиям, то при любом t должны соблюдаться условия:


Если бы обращался в ноль второй множитель, то решение равнялось бы нулю при всех значениях x и t. Поэтому, чтобы отыскать решения, не тождественно равные нулю (а только такие решения нас и интересуют) мы должны считать, что
X (0) = 0; X (l) = 0.
В результате для отыскания функции X (x) мы пришли к следующей задаче. Найти решение линейного дифференциального уравнения второго порядка:

при условиях:
X (0) = X (l) = 0.
Эта задача носит название задачи Штурма-Лиувилля.
Разумеется, эта задача при любом С имеет решение, тождественно равное нулю: X (x) = 0. Оказывается, однако, что при некоторых значениях постоянной С, эта задача имеет и ненулевые решения.
1. Пусть 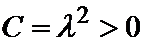 . Тогда общее решение уравнения
. Тогда общее решение уравнения
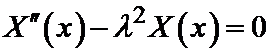
имеет вид:

Удовлетворим это решение граничным условиям:
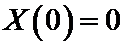
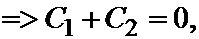
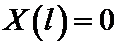

Так как определитель этой системы

не равен нулю, то система имеет единственное решение: C1=C2= 0.
Таким образом, в этом случае решений, отличных от тождественного нуля, не существует.
2. Пусть C= 0. Тогда уравнение становится особенно простым
 .
.
Его решение – это любой полином первой степени 
Подставляя в это решение граничные условия, имеем:
C 1=0; C 1 +C 2 l =0.
То есть, опять таки C1=C2= 0.
3. Пусть, наконец C=–l2< 0. Тогда уравнение будет следующим:
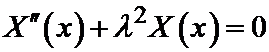 .
.
Его решение имеет вид:
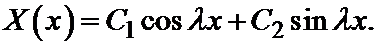
Подставляем граничные условия:
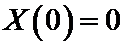 =>
=> 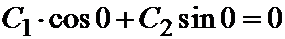 => C 1=0,
=> C 1=0,
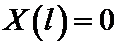 =>
=> 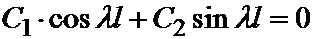 => C 2×sin ll =0.
=> C 2×sin ll =0.
Последнее равенство возможно, когда C 2¹0, оно будет удовлетворяться при sin ll =0.
То есть при 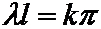 (k= ±1; ±2;….)
(k= ±1; ±2;….)
Итак, если 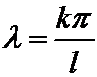 , т.е.
, т.е. 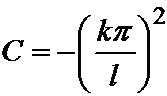 , то существуют решения уравнения колебаний струны, не равные тождественно нулю.
, то существуют решения уравнения колебаний струны, не равные тождественно нулю.
Решение, отвечающее некоторому фиксированному k обозначим через Xk (x). Оно имеет вид:
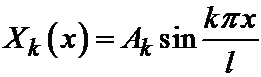 ,
,
где Ak – произвольная постоянная. Мы вправе в дальнейшем рассматривать только положительные значения k= 1,2,…, поскольку при отрицательных k получатся решения того же вида (ведь Ak – произвольные постоянные, которые могут иметь любые знаки).
Как мы видим, каждому значению  соответствует бесчисленное множество решений
соответствует бесчисленное множество решений  , отличающихся друг от друга постоянным множителем.
, отличающихся друг от друга постоянным множителем.
Величины  называются собственными числами, а функции
называются собственными числами, а функции  – собственными функциями дифференциального уравнения
– собственными функциями дифференциального уравнения  с краевыми условиями
с краевыми условиями  Именно с такими краевыми, условиями, поскольку, как мы увидим позднее, при других краевых условиях будут другие собственные функции, а не только
Именно с такими краевыми, условиями, поскольку, как мы увидим позднее, при других краевых условиях будут другие собственные функции, а не только  .
.
Итак, задача отыскания решения уравнения
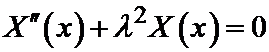
называется задачей Штурма-Лиувилля на собственные значения.
Видно, что найденные собственные функции 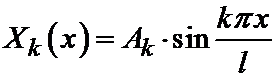 – это система тригонометрических функций (в данном случае система синусов). Эта система функций ортогональна на интервале (0, l), что известно из курса анализа.
– это система тригонометрических функций (в данном случае система синусов). Эта система функций ортогональна на интервале (0, l), что известно из курса анализа.
Теперь обратимся к отысканию функций T (t). Каждому собственному числу lk будет соответствовать своя функция Tk (t), определенная уравнением
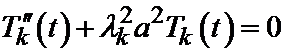 ,
,
или  .
.
Это уравнение имеет точно такое же решение, как и уравнение
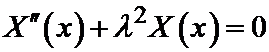 , то есть
, то есть
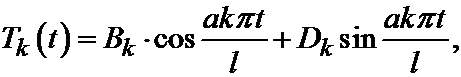
где Bk и Dk произвольные постоянные.
Подставляя найденные Xk (x) и Tk (t) в формулу 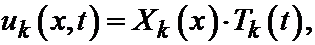 получим решение:
получим решение:
 Внося множитель Ak в скобку и обозначая
Внося множитель Ak в скобку и обозначая 
 запишем:
запишем:

Решения uk (x, t)называются собственными функциями задачи; соответствующие им колебания струны называются собственными колебаниями.
Сейчас осуществим вторую часть нашего плана: при помощи найденных собственных функций построим решение, удовлетворяющее начальным данным задачи.
В силу линейности и однородности уравнения колебаний струны, любая сумма решений uk (x,t) также будет решением:

Теперь будем выбирать произвольные постоянные  и
и  так, чтобы решение u (x,t) удовлетворяло первому начальному условию:
так, чтобы решение u (x,t) удовлетворяло первому начальному условию:  .
.
Дифференцируя этот ряд по t, имеем:

И подставляя t =0, удовлетворим решение второму начальному условию:

Эти формулы показывают, что величины  и
и  являются коэффициентами Фурье разложения функций j (x) и y(x) в ряды Фурье по синусам в интервале от 0 до l (0, l).
являются коэффициентами Фурье разложения функций j (x) и y(x) в ряды Фурье по синусам в интервале от 0 до l (0, l).
Вспоминая формулы для этих коэффициентов, найдём (чёрточки у  и
и  опустим):
опустим):

 .
.
Эти константы называются коэффициентами Фурье начальных данных. То есть мы получаем решение в следующем виде:

где 
 .
.
коэффициенты Фурье начальных данных.



 .
.
 .
. .
.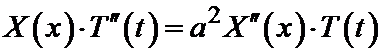 .
.


 .
.


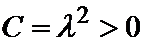 . Тогда общее решение уравнения
. Тогда общее решение уравнения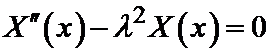

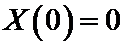
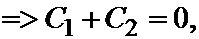
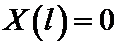


 .
.
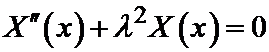 .
.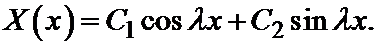
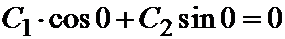 => C 1=0,
=> C 1=0,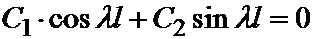 => C 2×sin ll =0.
=> C 2×sin ll =0.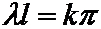 (k= ±1; ±2;….)
(k= ±1; ±2;….)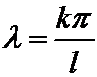 , т.е.
, т.е. 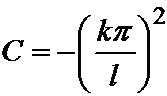 , то существуют решения уравнения колебаний струны, не равные тождественно нулю.
, то существуют решения уравнения колебаний струны, не равные тождественно нулю.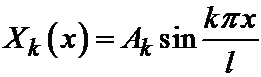 ,
, соответствует бесчисленное множество решений
соответствует бесчисленное множество решений  , отличающихся друг от друга постоянным множителем.
, отличающихся друг от друга постоянным множителем. – собственными функциями дифференциального уравнения
– собственными функциями дифференциального уравнения  с краевыми условиями
с краевыми условиями  Именно с такими краевыми, условиями, поскольку, как мы увидим позднее, при других краевых условиях будут другие собственные функции, а не только
Именно с такими краевыми, условиями, поскольку, как мы увидим позднее, при других краевых условиях будут другие собственные функции, а не только 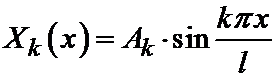 – это система тригонометрических функций (в данном случае система синусов). Эта система функций ортогональна на интервале (0, l), что известно из курса анализа.
– это система тригонометрических функций (в данном случае система синусов). Эта система функций ортогональна на интервале (0, l), что известно из курса анализа.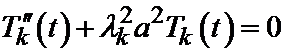 ,
, .
.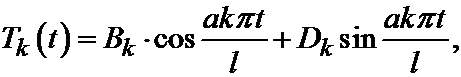
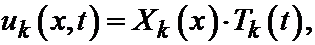 получим решение:
получим решение: Внося множитель Ak в скобку и обозначая
Внося множитель Ak в скобку и обозначая 
 запишем:
запишем:

 и
и  так, чтобы решение u (x,t) удовлетворяло первому начальному условию:
так, чтобы решение u (x,t) удовлетворяло первому начальному условию:  .
.

 являются коэффициентами Фурье разложения функций j (x) и y(x) в ряды Фурье по синусам в интервале от 0 до l (0, l).
являются коэффициентами Фурье разложения функций j (x) и y(x) в ряды Фурье по синусам в интервале от 0 до l (0, l).
 .
.