Приложение комплексных чисел в НАУКЕ
Ахтамов Антон Олегович, ученик 11 класса А
e-mail: [email protected] тел.5-14-62
МОУ «СОШ №9 г. Лесосибирска»
662547, г. Лесосибирск, 5а
Научный руководитель: Колотило Э.И.,
учитель математики высшей категории
В практике решения задач по физике и математике с помощью уравнений важное место занимают задачи, решаемые с помощью квадратных и кубических уравнений. Решая некоторые задачи из разделов динамики и механики, мы сталкиваемся с проблемой неудобства или невозможностью описания криволинейного движения тела, как на плоскости, так и в пространстве на поле действительных чисел. Помимо этого, решение многих задач из динамики и техники приводит к квадратным уравнениям с отрицательным дискриминантом и они имеют вид  . Указанные уравнения не имеют решения на области действительных чисел, однако эти задачи имеют вполне определённый физический смысл. Под термином «комплексная величина» мы будем понимать всякую величину, которая может быть изображена геометрически вектором на плоскости. Учения о комплексных числах находят применение во многих вопросах науки и техники. Например, Н. Е. Жуковский (1847-1921), отец русской авиации, широко использовал комплексные числа при разработке теории крыла, автором которой он является.
. Указанные уравнения не имеют решения на области действительных чисел, однако эти задачи имеют вполне определённый физический смысл. Под термином «комплексная величина» мы будем понимать всякую величину, которая может быть изображена геометрически вектором на плоскости. Учения о комплексных числах находят применение во многих вопросах науки и техники. Например, Н. Е. Жуковский (1847-1921), отец русской авиации, широко использовал комплексные числа при разработке теории крыла, автором которой он является.
В настоящие время комплексные числа широко используются для математического описания и решения многих вопросов физики и техники (в гидроаэродинамике, механике, электротехнике, атомной физике и др.)
Цель: изучить теорию комплексных чисел, свойства этих чисел и научиться применять их в решении прикладных задач по физике.
Объект исследования: комплексные числа.
Предмет исследования: приложение комплексных чисел в науке и технике, решение задач по физике.
Проблема: невозможность описания движения тела на поле действительных чисел
Гипотеза: комплексные числа - математическая модель для описания и изображения материальных точек в решении прикладных задач по физике.
Задачи исследования:
1) познакомиться с историей возникновения комплексного числа;
2) рассмотреть теоретические положения, связанные с понятием комплексного числа и его формой представления;
3) изучить арифметические операции над комплексными числами, а также формулы Муавра и Эйлера;
4) применить свойства комплексных чисел в решении задач динамики.
Методы исследования:
1) библиографический метод;
2) общенаучный метод (обобщение и систематизация научных положений);
3) метод моделирования и обоснования выводов;
4) метод классификации.
Экспериментальная работа
Теория комплексного числа находит широкое применение в области науки и техники. С помощью её можно решать многие физические задачи. В данной работе мы раскроем смысл комплексного числа, ознакомимся с его формами записи и изображения, арифметическими операциями, формулами и приложением комплексных чисел в науке и технике.
1. КОМПЛЕКСНЫЕ ЧИСЛА
Тригонометрическая форма комплексного числа
Абсцисса а и ордината b комплексного числа a+bi выражаются через модуль r и аргумент q. Формулами: a=r cos q; r=a/cos q; b=r sin q; r=b/sin q.
г - длина вектора (а+bi), q - угол, который он образует с положительным направлением оси абсцисс (см. рис. 1).
Поэтому всякое комплексное число можно представить в виде r(cosq+ isinq), где
r> 0, т.е. z=a+ bi или z=rcos q+ rsin q
Это выражение называется нормальной тригонометрической формой или тригонометрической формой комплексного числа.
Действия над комплексными числами
Сложение комплексных чисел
Определение. Суммой комплексных чисел а+ bi и a'+b'i называют комплексное число (а+ а') + (b+ b')i. Это определение подсказывается правилами действий с обычными многочленами.
Пример 1. (-3 + 5i) + (4- 8i)=l - 3i.
Пример 2. (2 + 0i) + (7 + 0i)=9 + 0i. Так как запись 2 + 0i обозначает то же, что и 2 наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
Вычитание комплексных чисел
Определение. Разностью комплексных чисел а+bi и а’+bi называется комплексное число (а- а') + (b- b')i.
Пример 1. (-5 + 2i) -(3- 5i) = -8 + 7i.
Пример 2. (3 + 2i) - (-3 + 2i) = 6 + 0i = 6.
Умножение комплексных чисел
Определение. Произведением комплексных чисел а+bi и a'+b'i называется комплексное число (аа' – bb') + (ab' + ba')i.
Замечание. На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i2= -1
Пример. (1 - 2i)(3 + 2i)=3 - 6i + 2i - 4i2 =3 - 6i + 2i + = 7- 4i.
Деление комплексных чисел
В соответствии с определением деления действительных чисел устанавливается следующее определение.
Определение. Чтобы разделить комплексное число a+bi на комплексное число
а' + b'i необходимо найти такое число x+yi, которое в произведении с a’+b’ даст a+ bi
Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряжённое со знаменателем
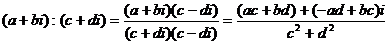
Пример 1. Найти частное (7 - 4i):(3 + 2i).
Записав дробь (7- 4i)/(3 + 2i), расширяем её на число 3 – 2i, сопряженное с 3 + 2i.
Получим: ((7-4i)(3-2i))/((3+2i)(3-2i))=(13-26i)/13=1-2i.
Формулы Эйлера и Муавра
В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а затем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707): (cosj+isinj)n =cos(jn)+isin(nj). Л. Эйлер вывел в 1748 году замечательную формулу: eix=cosx+isinx , которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число е в любую комплексную степень. Любопытно, например, что еip= -1. Таким образом можно находить синус и косинус от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.С помощью формулы Муавра выводится формула извлечения корня из комплексного числа.
Определение. Корнем n-й степени (n - натуральное число) из числа z называется такое число w, что wn=z.
Покажем, что действие извлечения корня во множестве комплексных чисел всегда выполнимо, и найдём значение w= 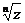 . Положим z=r(cosj+isinj), r>0 w=r(cosy+isiny), r>0. Тогда
. Положим z=r(cosj+isinj), r>0 w=r(cosy+isiny), r>0. Тогда
r n= (cos ny+isin ny) =r (cosj+isinj), rn=r, ny=j+2pk, k- целое, откуда
r= 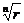 ,
, 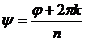 и
и 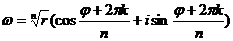 .
.
Приложение комплексных чисел в науке
В качестве приложения рассмотрим формулу Муавра. Она имеет большое практическое значение в тригонометрии, потому что позволяет выражать синусы косинусы углов (nx), где n- любое целое число, через простые функции sin x и cos x
Формула: (cosj+sinji)n= cosnj+ isinnj,
где i-мнимая часть комплексного числа, i2= -1
Пример.
cos3q+ isin3q=(cosq + isinq)3= oos3q + 3i cos2q sinq + 3i2 cosq sin2q +i3sin3q=
= cos3q – 3cosq sin2q + i(3cos2q sinq-sin3q)
Учитывая, что cosq – действительная часть, а sinq - мнимая получаем:
cos3q=cos3q - 3cosq sin2qsin3q=3cos2q sinq-sin3q
Таким же образом можно преобразовать sin4x, cos4x (sin5x, соз5х ит.д.) до выражений, содержащих sinx и соsx.
Применение комплексных функций действительного аргумента позволяет компактно изложить ряд вопросов из области кинематики и динамики.
Пусть точка Z перемещается по плоскости. Выбрав прямоугольную систему координат хОу, можем считать, что движение происходит по комплексной плоскости, а точка Z имеет комплексную координату z = x + iy, причем x =x(t), y = y(t), z = z(t). В каждый момент времени t точка Z будет иметь определенную скорость u(t), причем ее компоненты равны x(t) и y(t). Следовательно, в каждый момент времени t скорость точки Z характеризуется комплексным числом x(t)+iy(t), которое можно записать так: z(t). Аналогично ускорение w точки Z в каждый момент времени t задается комплексным числом
z(t) = x(t) + iy(t).
Числа z(t) и z(t) будем называть комплексной скоростью и комплексным ускорением точки Z.
Заключение
Комплексные числа, несмотря на всю их «лживость» и недействительность, находят себе широкое применение в математике, физике, химии, информатике и других областях науки. В настоящие время они широко используются в электромеханике, современном автомобиле- и судостроении, компьютерной и космической индустрии.
Результатом написания работы является овладение теорией комплексного числа, умение выполнять действия над комплексными числами и применять в решении задач.
Практическое приложение решаемых задач может найти применение для углубления знаний старшеклассников на факультативных занятиях, помимо этого данная работа может служить учебным пособием для вузов.
БИБЛИОГРАФИЯ
1. Балк, М.В. Реальные применения мнимых чисел / М.В. Балк, Г.Д. Балк, А.А. Полухин.- Киев: Радянськая школа, 1988.
2. Морозова, В.Д. Теория функций комплексного переменного / В.Д. Морозова.- М.: Издательство МГТУ им. Н.Э. Баумана, 2002.
3. Привалов, И.И. Введение в теорию функций комплексного переменного / И.И. Привалов.- М.: Гос. из-во техн.-теор. лит., 1954.
4. Туманов, С.И. Элементарная алгебра. Пособие для самообразования / С.И. Туманов.- М.: Просвещение, 1970.
5. Цыркин, М.Я. Краткий курс теории функций комплексного переменного / М.Я. Цыркин.- М.: Просвещение, 1964.
Приложение 1
Древнегреческие математики считали "настоящими" только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.
В III веке Архимед разработал систему обозначения вплоть до такого громадного как (108·10)16. Наряду с натуральными числами применяли дроби числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что
«... элементы чисел являются элементами всех вещей, и весь мир в целом является гармонией и числом». Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.
Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действий над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: нет такого числа х, чтобы х2=-9.
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида х 3+px+q=0 кубические и квадратные корни:
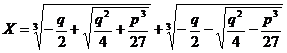
Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень (x3+3x-4=0), а если оно имеет три действительных корня (х3-7х+6=0), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени, Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины а, b, с, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.
Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений не имеющая решений во множестве действительных чисел, имеет решения вида х=5±  , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что  = -а.
= -а.
Кардано называл такие величины "чисто отрицательными" и даже '"софистически отрицательными", считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 год вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название "мнимые числа" ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века- Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа  (мнимой единицы). Этот символ вошёл во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа'' так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д., образующих единое целое.
(мнимой единицы). Этот символ вошёл во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа'' так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д., образующих единое целое.
В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.
Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а затем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707): (cosj+isinj)n =cos(jn)+isin(nj). С помощью этой формулы можно было так же вывести формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу: eix=cosx+isinx , которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число е в любую комплексную степень. Любопытно, например, что еip= -1. Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.
В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов. Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. Поэтому французский ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.
"Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраической формы иероглифы нелепых количеств" Л. Карно.
После создания теории комплексных чисел возник вопрос о существовании "гиперкомплексных" чисел - чисел с несколькими "мнимыми" единицами. Такую систему вида a+bi+cj+dk, где i2=j2=k2= -l, построил в 1843 году ирландский математик У. Гамильтон, который назвал их "кватернионами". Правила действия над кватернионами напоминает правила обычной алгебры, однако их умножение не обладает свойством коммутативности (переместительности): например, ij= k, a ji= -k.
ПРИЛОЖЕНИЕ 2
Сложение комплексных чисел
Пример 1. (-3 + 5i) + (4- 8i)=l - 3i.
Пример2. (2 + 0i) + (7 + 0i)=9 + 0i. Так как запись 2 + 0i обозначает то же, что и 2 наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Пример З. (0 + 2i) + (0 + 5i)=0 + 7i, т. e. 2i + 5i=7i.
Пример 4. (-2 + 3i) + (- 2-3i)= -4.
В примере 4 сумма двух комплексных чисел равна действительному числу. Два комплексных числа а+bi и а-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
Вычитание комплексных чисел
Пример 1. (-5 + 2i) -(3- 5i) = -8 + 7i.
Пример 2. (3 + 2i) - (-3 + 2i) = 6 + 0i = 6.
Умножение комплексных чисел
Пример 1. (1 - 2i)(3 + 2i)=3 - 6i + 2i - 4i2 =3 - 6i + 2i + = 7- 4i..
Пример 2. (a -bi)(a- bi)=a2+ b2 .
Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
Деление комплексных чисел
Пример. Найти частное (7 - 4i):(3 + 2i).
Записав дробь (7- 4i)/(3 + 2i), расширяем её на число 3 – 2i, сопряженное с 3 + 2i.
Получим: ((7-4i)(3-2i))/((3+2i)(3-2i))=(13-26i)/13=1-2i.
Пример1 предыдущего пункта даёт проверку:
(-2+5i)/(-3-4i)=((-2+5i)(-3+5i))/((-3-4i)(-3+4i))= ((-3-4i)(-3+4i))=(-14-23i)/25=
= -0,56-0,92i.
ПРИЛОЖЕНИЕ 3
ПРИЛОЖЕНИЕ 4
Приложение комплексных чисел в НАУКЕ
Ахтамов Антон Олегович, ученик 11 класса А
e-mail: [email protected] тел.5-14-62
МОУ «СОШ №9 г. Лесосибирска»
662547, г. Лесосибирск, 5а
Научный руководитель: Колотило Э.И.,
учитель математики высшей категории
В практике решения задач по физике и математике с помощью уравнений важное место занимают задачи, решаемые с помощью квадратных и кубических уравнений. Решая некоторые задачи из разделов динамики и механики, мы сталкиваемся с проблемой неудобства или невозможностью описания криволинейного движения тела, как на плоскости, так и в пространстве на поле действительных чисел. Помимо этого, решение многих задач из динамики и техники приводит к квадратным уравнениям с отрицательным дискриминантом и они имеют вид  . Указанные уравнения не имеют решения на области действительных чисел, однако эти задачи имеют вполне определённый физический смысл. Под термином «комплексная величина» мы будем понимать всякую величину, которая может быть изображена геометрически вектором на плоскости. Учения о комплексных числах находят применение во многих вопросах науки и техники. Например, Н. Е. Жуковский (1847-1921), отец русской авиации, широко использовал комплексные числа при разработке теории крыла, автором которой он является.
. Указанные уравнения не имеют решения на области действительных чисел, однако эти задачи имеют вполне определённый физический смысл. Под термином «комплексная величина» мы будем понимать всякую величину, которая может быть изображена геометрически вектором на плоскости. Учения о комплексных числах находят применение во многих вопросах науки и техники. Например, Н. Е. Жуковский (1847-1921), отец русской авиации, широко использовал комплексные числа при разработке теории крыла, автором которой он является.
В настоящие время комплексные числа широко используются для математического описания и решения многих вопросов физики и техники (в гидроаэродинамике, механике, электротехнике, атомной физике и др.)
Цель: изучить теорию комплексных чисел, свойства этих чисел и научиться применять их в решении прикладных задач по физике.
Объект исследования: комплексные числа.
Предмет исследования: приложение комплексных чисел в науке и технике, решение задач по физике.
Проблема: невозможность описания движения тела на поле действительных чисел
Гипотеза: комплексные числа - математическая модель для описания и изображения материальных точек в решении прикладных задач по физике.
Задачи исследования:
1) познакомиться с историей возникновения комплексного числа;
2) рассмотреть теоретические положения, связанные с понятием комплексного числа и его формой представления;
3) изучить арифметические операции над комплексными числами, а также формулы Муавра и Эйлера;
4) применить свойства комплексных чисел в решении задач динамики.
Методы исследования:
1) библиографический метод;
2) общенаучный метод (обобщение и систематизация научных положений);
3) метод моделирования и обоснования выводов;
4) метод классификации.
Экспериментальная работа
Теория комплексного числа находит широкое применение в области науки и техники. С помощью её можно решать многие физические задачи. В данной работе мы раскроем смысл комплексного числа, ознакомимся с его формами записи и изображения, арифметическими операциями, формулами и приложением комплексных чисел в науке и технике.
1. КОМПЛЕКСНЫЕ ЧИСЛА
История возникновения комплексного числа
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В частности для решения кубических уравнений вида х 3+px+q=0 используются формулы, содержащие квадратные и кубические корни. Путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа (см. приложение 1).
Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений не имеющая решений на множестве действительных чисел, имеет решения вида х= 5 ±  , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что  = -а.
= -а.
Кардано называл такие величины "чисто отрицательными" и даже "софистически отрицательными". В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название "мнимые числа" ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа  (мнимой единицы). Этот символ вошёл во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа'' так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, совокупность понятий, предметов, явлений и т. д., образующих единое целое (см. приложение 1).
(мнимой единицы). Этот символ вошёл во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа'' так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, совокупность понятий, предметов, явлений и т. д., образующих единое целое (см. приложение 1).



 . Указанные уравнения не имеют решения на области действительных чисел, однако эти задачи имеют вполне определённый физический смысл. Под термином «комплексная величина» мы будем понимать всякую величину, которая может быть изображена геометрически вектором на плоскости. Учения о комплексных числах находят применение во многих вопросах науки и техники. Например, Н. Е. Жуковский (1847-1921), отец русской авиации, широко использовал комплексные числа при разработке теории крыла, автором которой он является.
. Указанные уравнения не имеют решения на области действительных чисел, однако эти задачи имеют вполне определённый физический смысл. Под термином «комплексная величина» мы будем понимать всякую величину, которая может быть изображена геометрически вектором на плоскости. Учения о комплексных числах находят применение во многих вопросах науки и техники. Например, Н. Е. Жуковский (1847-1921), отец русской авиации, широко использовал комплексные числа при разработке теории крыла, автором которой он является.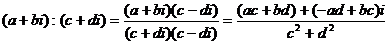
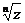 . Положим z=r(cosj+isinj), r>0 w=r(cosy+isiny), r>0. Тогда
. Положим z=r(cosj+isinj), r>0 w=r(cosy+isiny), r>0. Тогда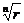 ,
, 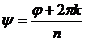 и
и 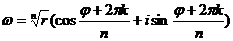 .
.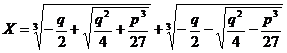
 , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что  = -а.
= -а. (мнимой единицы). Этот символ вошёл во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа'' так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д., образующих единое целое.
(мнимой единицы). Этот символ вошёл во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа'' так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д., образующих единое целое.


