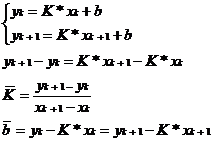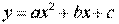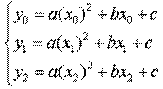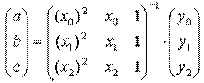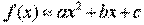Идея аппроксимации эмпирических данных. Невязки. Когда может возникать необходимость в поиске простейших эмпирических зависимостей? Как это сделать? Основные идеи формул расчета. Пример поиска конкретной функции.
Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей
| х
| x1
| х2
| …
| xn
|
| f(x)
| y1
| у2
| …
| yn
|
Необходимо найти функцию заданного вида: y=F(x), которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn.

Идея состоит в том, чтобы максимально приблизить данные из таблицы (на графике это звездочки) к прямой или любой другой функции, которая отобразит распределение этих точек наиболее близко.
Невязки. На графике это разница между точкой на прямой и «звездочкой» (получается опусканием перпендикуляра из звездочки к прямой). Невязка – разница между эмпирическими значениями и значениями аппроксимирующих линий; или разница между наблюденными аппроксимирующих функций. 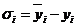 - невязки, где
- невязки, где 
Линейная функция (линейная регрессия).
Предположим, что связь между x и y линейна и искомую приближающую функцию будем искать в виде: 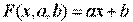
Найдем частные производные по параметрам: 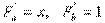
Подставим полученные соотношения в систему вида:
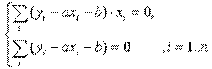
Далее имеем:
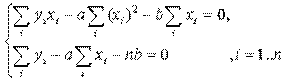
или, деля каждое уравнение на n:
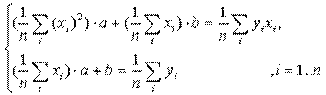
Введем обозначения:
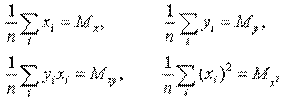
Тогда последняя система будет иметь вид:
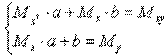
где xi, yi - значения из таблицы. Решив систему, получим значения параметров a и b, а следовательно, и конкретный вид линейной функции.
Поиск простейших эмпирических зависимостей необходим, чтобы упорядочить значения системы, заменить одну систему координат на другую, получив при этом приближённую функцию, которая в точках x1, x2, …, xn примет значения, как можно более близкие к табличным y1, y2, …, yn. Получение такой функции позволяет находить значения ф-ии f для нетабличных значений х, «сглаживая» результаты измерений величины у.
Основные идеи формул расчёта: К примеру, эмпирическая зависимость имеет вид: Y = axm. Прологарифмируем её: lny = lna + m lnx. Сделаем замену: Y = A + BX – получили линейную зависимость, где х = lnx и у = lnу – логарифмич замена. Переходим к билогарифмированию:
 После чего находим А и В и возвращаемся к первоначальным переменным.
После чего находим А и В и возвращаемся к первоначальным переменным.
В естествознании часто используется метод наименьших квадратов - метод оценивания параметров приближающей функции, кот сводит к min сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции.
Почему возникает необходимость аппроксимационного подхода при обработке натуральных данных? Методы аппроксимации табличных данных. Невязки. Метод наименьших квадратов. Графическая визуализация идеи метода наименьших квадратов.
Из курса математики известны 3 способа задания функциональных зависимостей:1) аналитический2) графический3) табличныйТабличный способ обычно возникает в результате эксперемента.Недостаток табличного задания функции заключается в том, что найдутся значения переменных которые неопределены таблицей. Для отыскания таких значений определяют приближающуюся функцию, называемой
аппроксмирующей, а действие замены аппроксимацией.
Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей
| х
| x1
| х2
| …
| xn
|
| f(x)
| y1
| у2
| …
| yn
|
Необходимо найти функцию заданного вида: y=F(x), которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn.
По таблице строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции.
Рассмотрим рисунок:

 У (а) У (b) У (с)
У (а) У (b) У (с)


































На рисунке изображены три ситуации:
1) график а - взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий.
2) график b - реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время, проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами.
3) график с - явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.
Метод наименьших квадратов
Метод наименьших квадратов (МНК) - Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции.
Задача приближения функции f: для функции f, заданной таблицей, найти функцию F определенного вида так, чтобы сумма квадратов Ф была наименьшей.
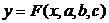
Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:
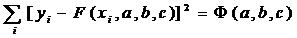
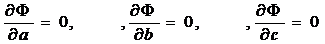 (1)
(1)
(2)
Пусть F(xi, a, b, c) = yi, i=1, 2,..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:
Эта сумма является функцией Ф(а, b, c) трех переменных (параметров a, b и c). Задача сводится к отысканию ее минимума. Используем необходимое условие экстремума:
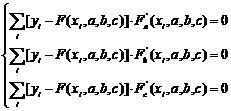 Получаем систему для определения неизвестных параметров a, b, c.
Получаем систему для определения неизвестных параметров a, b, c.
(3)
Решив эту систему получим конкретный вид искомой функции F(x, a, b, c). Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, а выразится лишь в изменении количества уравнений в системе (3).
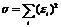 Значения найденной функции F(x, a, b, c) в точках х1, x2,..., xn, будут отличаться от табличных значений y1, y2,..., yn. Значения разностей yi-F(xi,a, b, c)=ei (i=1, 2,..., n) называются отклонениями измеренных значений y от вычисленных по формуле (1). Для найденной эмпирической формулы y=F(x) в соответствии с исходной таблицей можно, следовательно найти сумму квадратов отклонений, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (2) имеет наименьшее значение.
Значения найденной функции F(x, a, b, c) в точках х1, x2,..., xn, будут отличаться от табличных значений y1, y2,..., yn. Значения разностей yi-F(xi,a, b, c)=ei (i=1, 2,..., n) называются отклонениями измеренных значений y от вычисленных по формуле (1). Для найденной эмпирической формулы y=F(x) в соответствии с исходной таблицей можно, следовательно найти сумму квадратов отклонений, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (2) имеет наименьшее значение.
6. Для чего нужен гармонический анализ? Основные расчетные формулы. Интерпретация полученных результатов. Многие природные процессы являются периодическими, т.е. воспроизводятся в прежнем виде через определенный промежуток времени Т (смена времен года, смена дня и ночи, продолжительность светового дня и т.д.). С точки зрения математики, различные величины, связанные с рассматриваемыми периодическими процессами, по истечение периода Т возвращаются к своим прежним значениям и являются периодическими функциями от времени t: 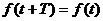
Гармонический анализ – это процесс разложения периодической функции в ряд Фурье (на гармоники). Гармоника (гармонические составляющие функции f(t)) – отдельные синусоидальные величины, входящие в состав тригонометрического ряда. Ибо периодическая функция f(t) периода Т (при этом составляющие синусоидальные величины разных частот) может быть представлена в виде суммы конечного или бесконечного множества синусоид. Интерпретация полученных результатов: с помощью гармонического анализа можно выделить низко-, средне- и высокочастотные колебания, а также оценить вклад отдельных гармоник в исследуемый процесс.
Задача гармонического анализа заключается в построении практически удобных методов для приближенного определения коэффициентов ряда Фурье или для непосредственного вычерчивания гармоник различных порядков для функции, заданной таблично.
Пусть ф-ия f(x) – периодическая с периодом 2π: f(x+2π)=f(x). Основная задача гармонического анализа – представить ф-цию f(x) в виде ряда: 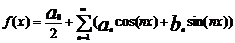 , где коэф. ряда определяется по формулам Эйлера-Фурье:
, где коэф. ряда определяется по формулам Эйлера-Фурье: 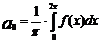 ;
;  ;
; 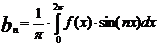
Полагая что 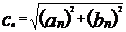 ,
, 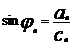 ,
,  ряд можно представить в виде:
ряд можно представить в виде: 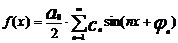 , где
, где 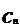 - амплитуда гармоники,
- амплитуда гармоники, 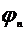 - фаза
- фаза
Для чего необходимо осреднение? Основные расчетные формулы метода скользящего среднего и экспоненциального сглаживания. Интерпретация полученных результатов. Достоинства и недостатки данных двух методов
Осреднение необходимо для исключения влияния на анализ флуктуаций – короткопериодические колебания, медленные постепенные изменения случайной переменной в течение всего анализируемого периода и колебания, хар-ся промежуточным временным масштабом.
Метод скользящей средней заключается в том, что для каждого аргумента берется средняя арифметическая на несколько соседних значениях функции.
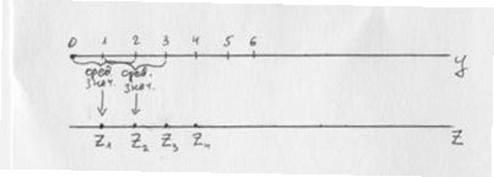
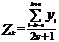 , т.е.
, т.е. 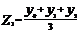 ;
; 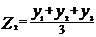
Пропадут первые v-точки и последние v-точки: 2v-точки.
Применяют для длинных рядов, где пропажа двух крайних 2v-точек ничего не решает. Характерно для физ.-географов и не характерно для эконом.географов, которые работают с небольшими рядами. Многоцелевой, легко программируемый метод, однако велика вероятность неточности.
Метод взвешенной скользящей средней является более точным, т.к. не связан с потерей крайних значений. Для этих целей добавляют с обеих концов ряда по два члена, расчет производится по формуле: 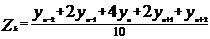
Метод экспоненциального сглаживания. Пусть есть некоторый ряд 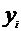 , где i=1,2,..n. Тогда расчетные формулы имеют вид:
, где i=1,2,..n. Тогда расчетные формулы имеют вид:
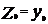 ; ;
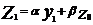
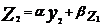 …
…
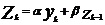
| α и β > 0
α+β=1
α ~ 0,1-0,3 (т.е. берут значение в этом пределе)
Чем меньше α, тем больше степень осреднения
|
Его преимущества заключаются в простоте вычислений, гибкости описаний динамик процессов. Метод экспоненциального сглаживания дает возможность получить оценку параметров тренда, хар-щих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения. Наибольшее применение метод нашел для коротких рядов в геоэкологии и эконом.географии. Для метода экспоненциального сглаживания основным и наиболее трудным моментом является выбор параметра сглаживания α и начальных условий.
Интерпретация полученных результатов: воспользовавшись рассмотренными методами, мы сократили, сжали набор полученных результатов и осреднили их, что избавило нас от ряда процессов обработки не столь важных результатов. (например, для оценки численности населения не так важно знать его каждодневное количество)
Описание динамических природных процессов. Решение диф уравнения как модель динамического процесса. Определение диф уравнения. Общее и частное решение. Смысл начальных условий для общего решения. Задача Коши.
Решение большинства задач естествознания после соответствующих упрощений сводится к решению уравнений, содержащих искомую функцию или несколько функций, зависящих от одного или нескольких аргументов. Дифференциальное уравнение, полученное в результате исследования какого-либо реального процесса или явления, называют дифференциальной моделью этого явления или процесса. Для решения прикладных задач созданы методы приближенного решения дифференциальных уравнений, которые условно можно подразделить на три основные группы:
1. Аналитические методы, применение которых даст решение дифференциальных уравнений в виде аналитической функции (метод Пикара);
2. Графические методы, дающие приближенное решение в виде графика (метод Эйлера);
3. Численные методы, когда искомая функция получается в виде таблицы (метод Рунге-Кутта).
Диф уравнение – уравнение, в кот неизвестная величина стоит под знаком производной. Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
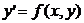 (1)
(1)
Решением дифференциального уравнения является некоторая функция y(x), которая при подстановке в выражение обращает его в тождество. Существует множество решений - частных решений - дифференциального уравнения (1), которые могут быть объединены и записаны в виде общего решения
y=y(x, C), (2)
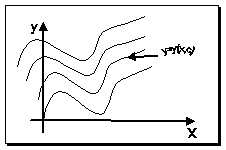 где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).
где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).
Для выбора одной кривой из семейства (частного решения y=y(x,c)) необходимо задать начальные условия, то есть одну точку на искомой кривой решения: y(x0)=y0 (3).
* Общее решение – это совокупность всех частных решений. Частное решение – график. Как правило, практическое значение имеет всегда частное решение дифференциального уравнения.
Мы рассматриваем модели, описываемые обыкновенными дифференциальными уравнениями, то есть уравнениями, в которых неизвестные функции зависят только от одной переменной. Если ф-ция зависит от многих переменных Z = z (x1,x2…xn), то это диф уравнение частных производных. Порядок старшей производной определяет порядок уравнения. Пр: ур-e второго порядка у'' = f(x, y, y').
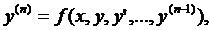 Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.
Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.
Если дифференциальное уравнение n-ого порядка:
тогда задача Коши состоит в нахождении решения y=y(x), удовлетворяющего начальным условиям у (х0) = у0, у' (х0) = у1, у'' (х0) = у2, …, у (n-1) (х0) = уn1.
Задача требует, чтобы мы искали не все решения, а только те, кот удовлетворяют уравнению. Решение уравнения у' = f(x, y) существует и единственно. Для этого достаточно, чтобы функция f(x,y) в правой части уравнения была непрерывна в рассматриваемой области по обоим аргументам и имела ограниченную частную производную.
Как составить дифференциальную модель природного процесса? Пример. Когда возникает необходимость численного решения дифференциального уравнения. Основная идея метода Эйлера. Основные расчетные формулы метода Эйлера. Основной недостаток метода Эйлера.
Построение диф. модели природного процесса: для начала задаём переменные; для построения находим уравнение изменения скорости природного процесса и решаем его. В результате получаем модель.
Пр.: На поверхности Земли нагрелись камни. Как быстро они остынут?
Решение: Пусть Т – температура камня. 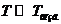
Найдём скорость охлаждения камней: 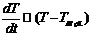 ,
, 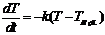 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const.
 => Проинтегрируем:
=> Проинтегрируем: 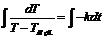 . Решив интегралы, получаем:
. Решив интегралы, получаем: 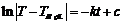 =>
=> 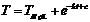 .
.
При t=0, Т=Т0, 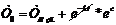 , где
, где 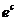 - В. В= Т0-Т возд =>
- В. В= Т0-Т возд => 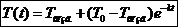 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
В основе метода Эйлера лежит идея графического построения решения диф-ного уравнения. Этот метод одновременно дает и способ нахождения искомой функции в численной (табличной) форме.
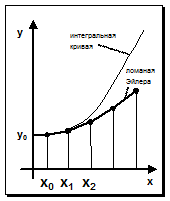 Идея метода заключается в том, что на малом промежутке изменения независимой переменной
Идея метода заключается в том, что на малом промежутке изменения независимой переменной 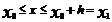 (где h – шаг таблицы) интегральная кривая диф-ного уравнения
(где h – шаг таблицы) интегральная кривая диф-ного уравнения  заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 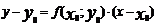 . Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.
Рабочая формула для определения значения y имеет вид: 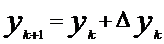 , где
, где 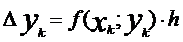 ,
, 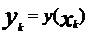 ,
, 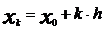
Основной плюс: легко пишется и мало ошибок. Обеспечивает требуемую точность только для аналитического вида части функции. Метод Эйлера обладает малой точностью, к тому же погрешность каждого шага систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета – с шагом h и шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными. Ошибка метода пропорциональна h2. Существуют различные уточнения метода Эйлера, повышающие его точность так, что ошибка метода становится пропорциональной h3.
Как составить дифференциальную модель природного процесса? Пример. Когда возникает необходимость численного решения дифференциального уравнения. Основная идея и недостаток метода Эйлера. Метод Рунге-Кутта. Основная идея метода Рунге-Кутта. Расчётные формулы. Главное достоинство метода Рунге-Кутта.
Построение диф. модели природного процесса: для начала задаём переменные; для построения находим уравнение изменения скорости природного процесса и решаем его. В результате получаем модель.
Пр.: На поверхности Земли нагрелись камни. Как быстро они остынут?
Решение: Пусть Т – температура камня. 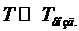
Найдём скорость охлаждения камней: 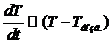 ,
, 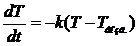 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const.
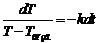 => Проинтегрируем:
=> Проинтегрируем: 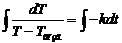 . Решив интегралы, получаем:
. Решив интегралы, получаем: 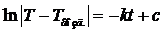 =>
=>  .
.
При t=0, Т=Т0, 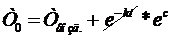 , где
, где 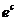 - В. В= Т0-Т возд =>
- В. В= Т0-Т возд => 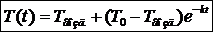 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
Численное решение дифференциального уравнения требуется тогда, когда искомая функция получается в виде таблицы (метод Рунге-Кутта).
В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод даёт одновременно и способ нахождения искомой функции в численной (табличной) форме. Идея метода заключается в том, что на малом промежутке изменения независимой переменной 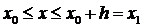 интегральная кривая дифференциального уравнения
интегральная кривая дифференциального уравнения 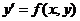 заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 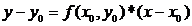 . Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.
+: легко пишется и мало ошибок;
-: малая точность и погрешность каждого нового шага систематически возрастает. Ошибка метода пропорциональна h2. Обеспечивает требуемую точность только для части функций аналитического вида.
Метод Рунге-Кутта. Пусть дано диф. Уравнение первого порядка: 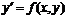 с начальными условиями
с начальными условиями 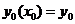 . Выберем шаг h и для кратности введем обозначения
. Выберем шаг h и для кратности введем обозначения  ,
, 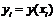 ,
, 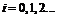 .
.
В вычислительной практике наиболее часто используется метод Рунге-Кутта.
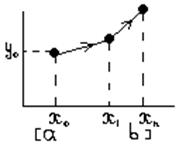
По методу вычисляют 5 вспомогательных коэффициентов 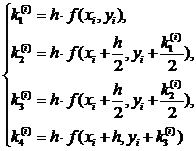
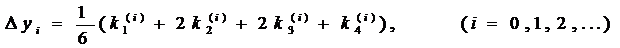 Последовательные приближения yi искомой функции y определяются по формуле:
Последовательные приближения yi искомой функции y определяются по формуле:
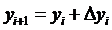 где (5)
где (5)
Смысл метода: при подстановке этих коэффициентов в формулу Тэйлора все члены до 5-го порядка уничтожаются!
+: в этом случае погрешность на шаге пропорциональна h5. Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение, полученное методом Рунге-Кутта, будет близким к точному.
Геометрически смысл использования метода Рунге-Кутта с расчетными формулами состоит в следующем: мы колеблемся вокруг точки, выбранной нами на пути движения из точки (x0,y0) в точку (x1,y1). Эти колебания отвечают рассчитанным выше коэффициентам. Потом четыре полученных направления усредняются в соответствии с последней из формул (5). На этом окончательном направлении и выбирается очередная точка.
Как составить дифференциальную модель периодического природного процесса? Пример. Основная идея численного метода решения дифференциального уравнения второго порядка. Описание метода Рунге-Кутта для системы дифференциальных уравнений. Математический маятник.
Для построения модели периодического характера необходимо выявить основные факторы, которые оказывают влияние на изучаемый процесс, и которые необходимо отразить в модели. Общее уравнение: 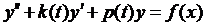 , где
, где 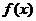 - вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
- вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
af - смертность среди хищников
bf - рождаемость хищников
cyf - воздействия внешней среды
cf - рожденные жертв
df - численность съеденной популяции
ef - рождаемость жертв
Составляем систему уравнений, характеризующих численность и тех и других на определённый период времени и получаем модель:

Решаем систему с помощью метода Рунге-Кутта. В результате строим графики динамики численности хищников и жертв за период времени t.
Математи́ческий ма́ятник — гармонический осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Уравнение математического маятника без затухания (т.к. справа 0): 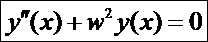 , где w-собственная частота гармонического осциллятора. Уравнение вида
, где w-собственная частота гармонического осциллятора. Уравнение вида 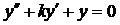 - математический маятник с трением, где k – коэф. трения. Уравнение вида
- математический маятник с трением, где k – коэф. трения. Уравнение вида 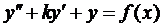 - с вынуждающей функцией.
- с вынуждающей функцией.
Общее решение математического маятника: 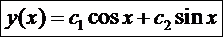 , с1, с2 – постоянные интегрирования. Пр.: При
, с1, с2 – постоянные интегрирования. Пр.: При 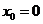 , ->
, ->  и
и  .
.
Приближённое решение математического маятника: Условие:
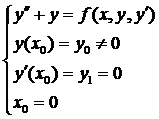
Пусть 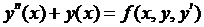 , где
, где 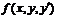 -трение маятника о воздух, или толчок маятника рукой. Пусть
-трение маятника о воздух, или толчок маятника рукой. Пусть  , тогда
, тогда 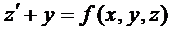 .
.
Получаем систему: 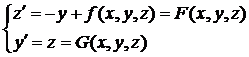
Решение системы диф. уравнений методом Рунге-Кутта – простейшее решение математического маятника:
Для решения надо найти 8 коэффициентов (2 набора k и m):

Для коэффициентов m в левой части k заменяем на m и SY на SZ, а в правой - F на G.
Составляем систему решений:
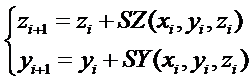
Основная идея численного метода решения дифференциального уравнения второго порядка-переход от див. уравнения n-го порядка к системе уравнений 1-го порядка:
Пр.: пусть 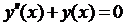 . Обозначим
. Обозначим 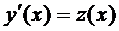 , тогда
, тогда 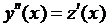 . Подставим:
. Подставим:
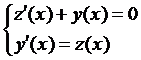
Пр.: 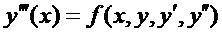 Обозначим:
Обозначим: 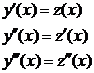
Подставим 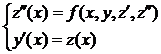
Ещё одна замена: 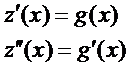 Получаем:
Получаем: 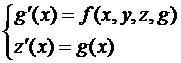
А. Модель радиоактивного распада. Основная идея модели. Основной недостаток модели. Как использовать модель для прогноза?
Пусть на какой-то территории выпало какое-то количество тонн радия. Какое количество радия распадётся за первые 100 лет?
Решение: пусть x – количество выпавшего радия, t – время, x(t) – скорость распада радия. При t=0, х(0)=х0.
Найдём скорость распада радия: 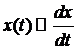 Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).
Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).
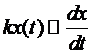 , где k – постоянно.
, где k – постоянно. 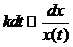 ->
-> 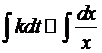 Решив эти интегралы, получаем:
Решив эти интегралы, получаем:
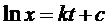 .
.
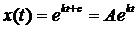 -первоначальная модель решения, но у нас нет А и k.
-первоначальная модель решения, но у нас нет А и k.
Находим их: 1. 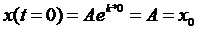 ->
->  .
.
2. 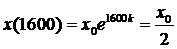 ->
-> 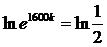 ->
->  ->
-> 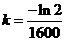 .
.
Итак, модель выглядит так:
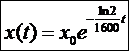 . Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.
. Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.
Идея модели dx/dt = x
Когда может возникнуть необходимость в линейной (квадратичной) интерполяции? И как это сделать? Основные формулы линейной (квадратичной) интерполяции?
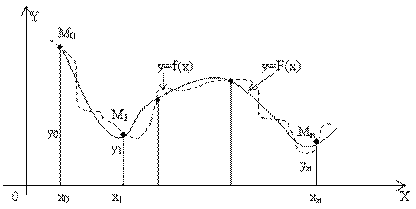
Пусть известные значения некоторой функции f образуют следующую таблицу:
| х
| x0
| x1
| …
| xn
|
| f(x)
| y0
| y1
| …
| yn
|
При этом требуется получить значение функции f для такого значения аргумента х, которое входит в отрезок [x0;xn], но не совпадает ни с одним из значений xi (i=0,1,…,n). Проще говоря, задача интерполяции состоит в том, чтобы понять какое у в точке х, еслт нет такого значения в измеренных данных.
Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках xi(i=0, 1, 2, …, n), т.е.
F(x0)=y0, F(x1)=y1, …, F(xn)=yn
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), а точки x0, x1, …, xn – узлами интерполяции. Геометрически это означает, что нужно найти кривую y=F(x) некоторого определенного типа, проходящую через заданную систему точек Mi(xi,yi) (i=0,1,2,…,n). В случае, если x не принадлежит [x0, xn] нахождение искомой функции называют экстраполяцией. В дальнейшем, под термином интерполяция будем понимать как первую, так и вторую операции.
Наиболее удобной в практическом использовании функцией является алгебраический многочлен степени n:
Pn(x)=a0xn + a1xn-1 + … + an-1x + an
Чтобы задать многочлен n-ой степени достаточно задать его n+1 коэффициент. Значения многочлена просто вычисляются, его легко продифференцировать, проинтегрировать и т.д. Поэтому алгебраические многочлены нашли широкое применение для приближения функций.
1.Линейная интерполяция.
Итак, пусть мы имеем функцию, заданную таблично. Решая задачу интерполяции, найдем в таблице два соседних значения аргумента (обозначим их хk и xk+1), между которыми лежит заданное значение х (хk<x<xk+1), пусть yk=f(xk) и yk+1=f(xk+1) – соответствующие им значения функции. Будем считать, что в промежутке (хk, xk+1) данную функцию с достаточной степенью точности можно заменить линейной функцией, т.е. дугу графика функции можно заменить стягивающей ее хордой. Такая замена называется линейной интерполяцией.
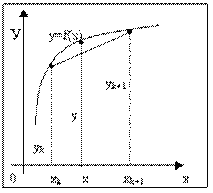
Уравнение прямой – у=K*х +b.
По графику
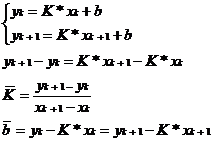
«+» - не даст больших погрешностей
«-» - нельзя применять когда интервалы между измерениями разные.
2.Квадратичная интерполяция.
Пусть снова дана функция f(x), заданная таблично. Считая, что на промежутке (xk, xk+2) данную функцию с достаточной степенью точности можно заменить квадратичной функцией, то есть часть графика функции можно заменить параболой (см. рис. 3), необходимо найти значение функции f(x) в некоторой точке x, принадлежащей интервалу (xk, xk+2).
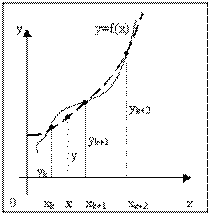
Будем искать квадратичную функцию в следующем виде: 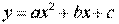
Исходя из условия совпадения значений искомой квадратичной функции с табличными значениями функции в трех заданных точках, составим следующую систему уравнений:
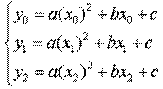
Это система трех линейных уравнений с тремя неизвестными a, b и с. Ее определитель не равен 0 (если только точки не лежат на одной прямой). Решая составленную систему уравнений матричным способом, получим следующую зависимость для коэффициентов а, b и с:
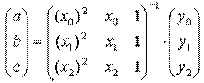
Таким образом значение функции f(х) в точке х можно приближенно считать равным
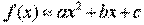
Идея аппроксимации эмпирических данных. Невязки. Когда может возникать необходимость в поиске простейших эмпирических з<




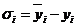 - невязки, где
- невязки, где 
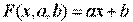
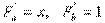
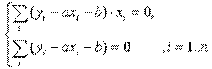
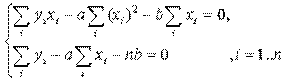
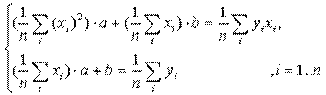
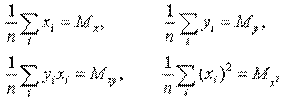
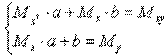
 После чего находим А и В и возвращаемся к первоначальным переменным.
После чего находим А и В и возвращаемся к первоначальным переменным.


 У (а) У (b) У (с)
У (а) У (b) У (с)




















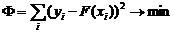
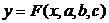 Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:
Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:
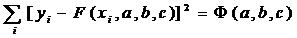
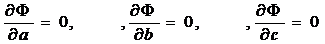 (1)
(1)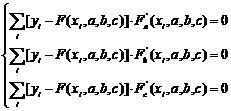 Получаем систему для определения неизвестных параметров a, b, c.
Получаем систему для определения неизвестных параметров a, b, c.
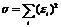 Значения найденной функции F(x, a, b, c) в точках х1, x2,..., xn, будут отличаться от табличных значений y1, y2,..., yn. Значения разностей yi-F(xi,a, b, c)=ei (i=1, 2,..., n) называются отклонениями измеренных значений y от вычисленных по формуле (1). Для найденной эмпирической формулы y=F(x) в соответствии с исходной таблицей можно, следовательно найти сумму квадратов отклонений, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (2) имеет наименьшее значение.
Значения найденной функции F(x, a, b, c) в точках х1, x2,..., xn, будут отличаться от табличных значений y1, y2,..., yn. Значения разностей yi-F(xi,a, b, c)=ei (i=1, 2,..., n) называются отклонениями измеренных значений y от вычисленных по формуле (1). Для найденной эмпирической формулы y=F(x) в соответствии с исходной таблицей можно, следовательно найти сумму квадратов отклонений, которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (2) имеет наименьшее значение.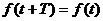
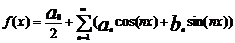 , где коэф. ряда определяется по формулам Эйлера-Фурье:
, где коэф. ряда определяется по формулам Эйлера-Фурье: 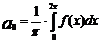 ;
;  ;
; 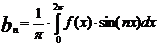
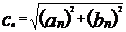 ,
, 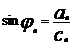 ,
,  ряд можно представить в виде:
ряд можно представить в виде: 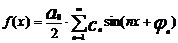 , где
, где 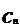 - амплитуда гармоники,
- амплитуда гармоники, 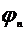 - фаза
- фаза
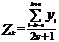 , т.е.
, т.е. 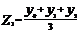 ;
; 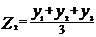
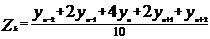
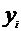 , где i=1,2,..n. Тогда расчетные формулы имеют вид:
, где i=1,2,..n. Тогда расчетные формулы имеют вид: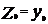 ;
;
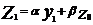
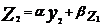 …
…
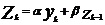
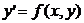 (1)
(1) где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).
где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).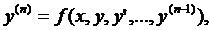 Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.
Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.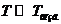
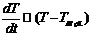 ,
, 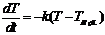 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const. => Проинтегрируем:
=> Проинтегрируем: 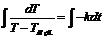 . Решив интегралы, получаем:
. Решив интегралы, получаем: 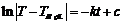 =>
=> 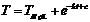 .
.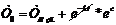 , где
, где 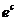 - В. В= Т0-Т возд =>
- В. В= Т0-Т возд => 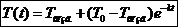 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня. Идея метода заключается в том, что на малом промежутке изменения независимой переменной
Идея метода заключается в том, что на малом промежутке изменения независимой переменной 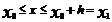 (где h – шаг таблицы) интегральная кривая диф-ного уравнения
(где h – шаг таблицы) интегральная кривая диф-ного уравнения  заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 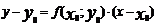 . Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.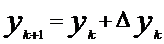 , где
, где 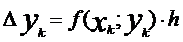 ,
, 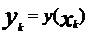 ,
, 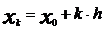
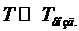
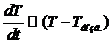 ,
, 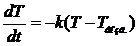 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const.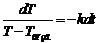 => Проинтегрируем:
=> Проинтегрируем: 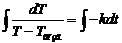 . Решив интегралы, получаем:
. Решив интегралы, получаем: 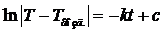 =>
=>  .
.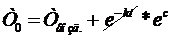 , где
, где 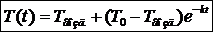 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.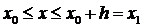 интегральная кривая дифференциального уравнения
интегральная кривая дифференциального уравнения 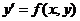 заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 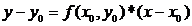 . Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.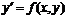 с начальными условиями
с начальными условиями 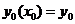 . Выберем шаг h и для кратности введем обозначения
. Выберем шаг h и для кратности введем обозначения  ,
, 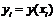 ,
, 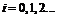 .
.
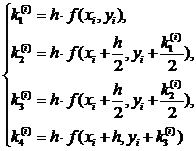
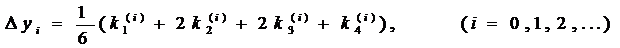 Последовательные приближения yi искомой функции y определяются по формуле:
Последовательные приближения yi искомой функции y определяются по формуле: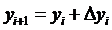 где (5)
где (5)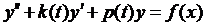 , где
, где 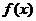 - вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
- вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
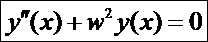 , где w-собственная частота гармонического осциллятора. Уравнение вида
, где w-собственная частота гармонического осциллятора. Уравнение вида 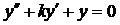 - математический маятник с трением, где k – коэф. трения. Уравнение вида
- математический маятник с трением, где k – коэф. трения. Уравнение вида 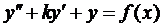 - с вынуждающей функцией.
- с вынуждающей функцией.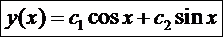 , с1, с2 – постоянные интегрирования. Пр.: При
, с1, с2 – постоянные интегрирования. Пр.: При 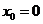 , ->
, ->  и
и  .
.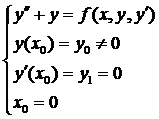
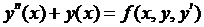 , где
, где 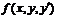 -трение маятника о воздух, или толчок маятника рукой. Пусть
-трение маятника о воздух, или толчок маятника рукой. Пусть  , тогда
, тогда 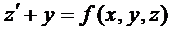 .
.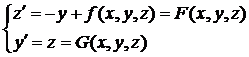

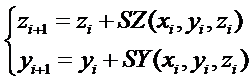
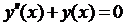 . Обозначим
. Обозначим 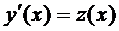 , тогда
, тогда 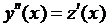 . Подставим:
. Подставим: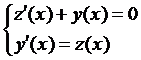
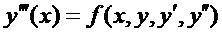 Обозначим:
Обозначим: 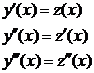
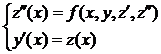
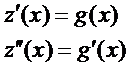 Получаем:
Получаем: 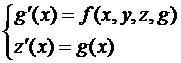
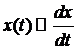 Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).
Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).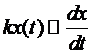 , где k – постоянно.
, где k – постоянно. 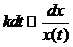 ->
-> 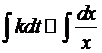 Решив эти интегралы, получаем:
Решив эти интегралы, получаем: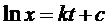 .
.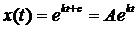 -первоначальная модель решения, но у нас нет А и k.
-первоначальная модель решения, но у нас нет А и k.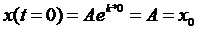 ->
->  .
.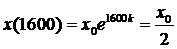 ->
-> 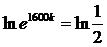 ->
->  ->
-> 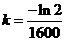 .
.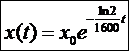 . Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.
. Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.