Тренд – медленный изменяющийся процесс. Пр.: в экономике – инфляция.
Удаление тренда производят в самом начале обработки экспериментальных данных с целью приведения данных в более корректную формулу, и последующего правильного анализа.
Удаление линейного тренда. Этапы:
1. Составление уравнения линейной регрессии: Y=ax+b.
2. Удаление линейного тренда из исходного временного ряда: 
 .
.
3. Гармонический анализ для ряда 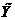 .
.
Интерпретация полученных результатов: удалив тренд, мы тем самым разделяем саму кривую тренда и колебательную кривую вдоль этого тренда. Это позволяет, так сказать, «очистить» необходимую зависимость, функцию от воздействия медленного изменяющегося во времени процесса. После удаления тренда наряду с основными гармониками мы получаем возможность оценить ещё вклад второстепенных гармоник, которые в первоначальных графиках «гасились» трендом.
Описание динамических природных процессов. Решение диф уравнения как модель динамического процесса. Определение диф уравнения. Общее и частное решение. Смысл начальных условий для общего решения. Задача Коши.
Решение большинства задач естествознания после соответствующих упрощений сводится к решению уравнений, содержащих искомую функцию или несколько функций, зависящих от одного или нескольких аргументов. Дифференциальное уравнение, полученное в результате исследования какого-либо реального процесса или явления, называют дифференциальной моделью этого явления или процесса. Для решения прикладных задач созданы методы приближенного решения дифференциальных уравнений, которые условно можно подразделить на три основные группы:
1. Аналитические методы, применение которых даст решение дифференциальных уравнений в виде аналитической функции (метод Пикара);
2. Графические методы, дающие приближенное решение в виде графика (метод Эйлера);
3. Численные методы, когда искомая функция получается в виде таблицы (метод Рунге-Кутта).
Диф уравнение – уравнение, в кот неизвестная величина стоит под знаком производной. Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
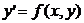 (1)
(1)
Решением дифференциального уравнения является некоторая функция y(x), которая при подстановке в выражение обращает его в тождество. Существует множество решений - частных решений - дифференциального уравнения (1), которые могут быть объединены и записаны в виде общего решения
y=y(x, C), (2)
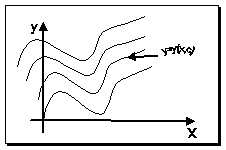 где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).
где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).
Для выбора одной кривой из семейства (частного решения y=y(x,c)) необходимо задать начальные условия, то есть одну точку на искомой кривой решения: y(x0)=y0 (3).
* Общее решение – это совокупность всех частных решений. Частное решение – график. Как правило, практическое значение имеет всегда частное решение дифференциального уравнения.
Мы рассматриваем модели, описываемые обыкновенными дифференциальными уравнениями, то есть уравнениями, в которых неизвестные функции зависят только от одной переменной. Если ф-ция зависит от многих переменных Z = z (x1,x2…xn), то это диф уравнение частных производных. Порядок старшей производной определяет порядок уравнения. Пр: ур-e второго порядка у'' = f(x, y, y').
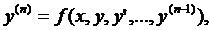 Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.
Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.
Если дифференциальное уравнение n-ого порядка:
тогда задача Коши состоит в нахождении решения y=y(x), удовлетворяющего начальным условиям у (х0) = у0, у' (х0) = у1, у'' (х0) = у2, …, у (n-1) (х0) = уn1.
Задача требует, чтобы мы искали не все решения, а только те, кот удовлетворяют уравнению. Решение уравнения у' = f(x, y) существует и единственно. Для этого достаточно, чтобы функция f(x,y) в правой части уравнения была непрерывна в рассматриваемой области по обоим аргументам и имела ограниченную частную производную.
Как составить дифференциальную модель природного процесса? Пример. Когда возникает необходимость численного решения дифференциального уравнения. Основная идея метода Эйлера. Основные расчетные формулы метода Эйлера. Основной недостаток метода Эйлера.
Построение диф. модели природного процесса: для начала задаём переменные; для построения находим уравнение изменения скорости природного процесса и решаем его. В результате получаем модель.
Пр.: На поверхности Земли нагрелись камни. Как быстро они остынут?
Решение: Пусть Т – температура камня. 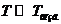
Найдём скорость охлаждения камней: 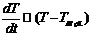 ,
, 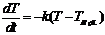 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const.
 => Проинтегрируем:
=> Проинтегрируем: 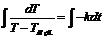 . Решив интегралы, получаем:
. Решив интегралы, получаем: 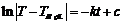 =>
=> 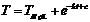 .
.
При t=0, Т=Т0, 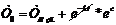 , где
, где 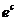 - В. В= Т0-Т возд =>
- В. В= Т0-Т возд => 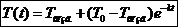 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
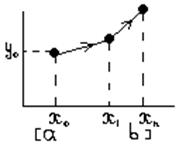
В основе метода Эйлера лежит идея графического построения решения диф-ного уравнения. Этот метод одновременно дает и способ нахождения искомой функции в численной (табличной) форме.
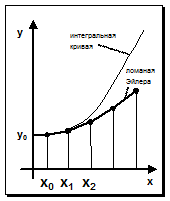 Идея метода заключается в том, что на малом промежутке изменения независимой переменной
Идея метода заключается в том, что на малом промежутке изменения независимой переменной 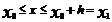 (где h – шаг таблицы) интегральная кривая диф-ного уравнения
(где h – шаг таблицы) интегральная кривая диф-ного уравнения  заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 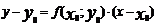 . Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.
Рабочая формула для определения значения y имеет вид: 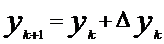 , где
, где 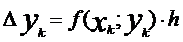 ,
, 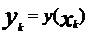 ,
, 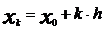
Основной плюс: легко пишется и мало ошибок. Обеспечивает требуемую точность только для аналитического вида части функции. Метод Эйлера обладает малой точностью, к тому же погрешность каждого шага систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета – с шагом h и шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными. Ошибка метода пропорциональна h2. Существуют различные уточнения метода Эйлера, повышающие его точность так, что ошибка метода становится пропорциональной h3.
Как составить дифференциальную модель природного процесса? Пример. Когда возникает необходимость численного решения дифференциального уравнения. Основная идея и недостаток метода Эйлера. Метод Рунге-Кутта. Основная идея метода Рунге-Кутта. Расчётные формулы. Главное достоинство метода Рунге-Кутта.
Построение диф. модели природного процесса: для начала задаём переменные; для построения находим уравнение изменения скорости природного процесса и решаем его. В результате получаем модель.
Пр.: На поверхности Земли нагрелись камни. Как быстро они остынут?
Решение: Пусть Т – температура камня. 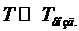
Найдём скорость охлаждения камней: 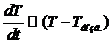 ,
, 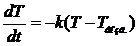 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const.
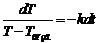 => Проинтегрируем:
=> Проинтегрируем: 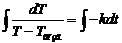 . Решив интегралы, получаем:
. Решив интегралы, получаем: 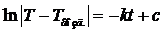 =>
=>  .
.
При t=0, Т=Т0, 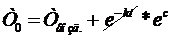 , где
, где 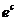 - В. В= Т0-Т возд =>
- В. В= Т0-Т возд => 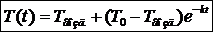 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
Численное решение дифференциального уравнения требуется тогда, когда искомая функция получается в виде таблицы (метод Рунге-Кутта).
В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод даёт одновременно и способ нахождения искомой функции в численной (табличной) форме. Идея метода заключается в том, что на малом промежутке изменения независимой переменной 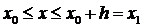 интегральная кривая дифференциального уравнения
интегральная кривая дифференциального уравнения 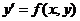 заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 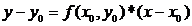 . Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.
+: легко пишется и мало ошибок;
-: малая точность и погрешность каждого нового шага систематически возрастает. Ошибка метода пропорциональна h2. Обеспечивает требуемую точность только для части функций аналитического вида.
Метод Рунге-Кутта. Пусть дано диф. Уравнение первого порядка: 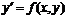 с начальными условиями
с начальными условиями 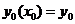 . Выберем шаг h и для кратности введем обозначения
. Выберем шаг h и для кратности введем обозначения  ,
, 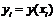 ,
, 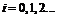 .
.
В вычислительной практике наиболее часто используется метод Рунге-Кутта.
По методу вычисляют 5 вспомогательных коэффициентов 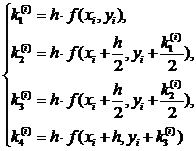
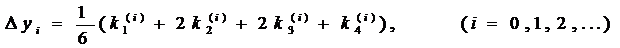 Последовательные приближения yi искомой функции y определяются по формуле:
Последовательные приближения yi искомой функции y определяются по формуле:
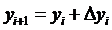 где (5)
где (5)
Смысл метода: при подстановке этих коэффициентов в формулу Тэйлора все члены до 5-го порядка уничтожаются!
+: в этом случае погрешность на шаге пропорциональна h5. Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение, полученное методом Рунге-Кутта, будет близким к точному.
Геометрически смысл использования метода Рунге-Кутта с расчетными формулами состоит в следующем: мы колеблемся вокруг точки, выбранной нами на пути движения из точки (x0,y0) в точку (x1,y1). Эти колебания отвечают рассчитанным выше коэффициентам. Потом четыре полученных направления усредняются в соответствии с последней из формул (5). На этом окончательном направлении и выбирается очередная точка.
Как составить дифференциальную модель периодического природного процесса? Пример. Основная идея численного метода решения дифференциального уравнения второго порядка. Описание метода Рунге-Кутта для системы дифференциальных уравнений. Математический маятник.
Для построения модели периодического характера необходимо выявить основные факторы, которые оказывают влияние на изучаемый процесс, и которые необходимо отразить в модели. Общее уравнение: 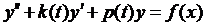 , где
, где 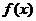 - вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
- вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
af - смертность среди хищников
bf - рождаемость хищников
cyf - воздействия внешней среды
cf - рожденные жертв
df - численность съеденной популяции
ef - рождаемость жертв
Составляем систему уравнений, характеризующих численность и тех и других на определённый период времени и получаем модель:

Решаем систему с помощью метода Рунге-Кутта. В результате строим графики динамики численности хищников и жертв за период времени t.
Математи́ческий ма́ятник — гармонический осциллятор, представляющий собой механическую систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Уравнение математического маятника без затухания (т.к. справа 0): 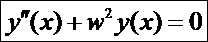 , где w-собственная частота гармонического осциллятора. Уравнение вида
, где w-собственная частота гармонического осциллятора. Уравнение вида 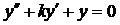 - математический маятник с трением, где k – коэф. трения. Уравнение вида
- математический маятник с трением, где k – коэф. трения. Уравнение вида 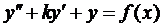 - с вынуждающей функцией.
- с вынуждающей функцией.
Общее решение математического маятника: 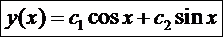 , с1, с2 – постоянные интегрирования. Пр.: При
, с1, с2 – постоянные интегрирования. Пр.: При 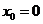 , ->
, ->  и
и  .
.
Приближённое решение математического маятника: Условие:
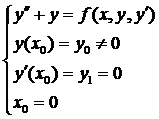
Пусть 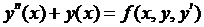 , где
, где 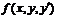 -трение маятника о воздух, или толчок маятника рукой. Пусть
-трение маятника о воздух, или толчок маятника рукой. Пусть  , тогда
, тогда 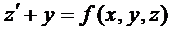 .
.
Получаем систему: 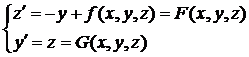
Решение системы диф. уравнений методом Рунге-Кутта – простейшее решение математического маятника:
Для решения надо найти 8 коэффициентов (2 набора k и m):

Для коэффициентов m в левой части k заменяем на m и SY на SZ, а в правой - F на G.
Составляем систему решений:
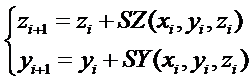
Основная идея численного метода решения дифференциального уравнения второго порядка-переход от див. уравнения n-го порядка к системе уравнений 1-го порядка:
Пр.: пусть 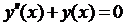 . Обозначим
. Обозначим 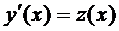 , тогда
, тогда 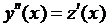 . Подставим:
. Подставим:
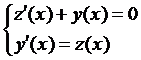
Пр.: 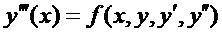 Обозначим:
Обозначим: 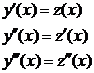
Подставим 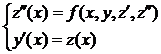
Ещё одна замена: 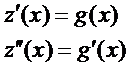 Получаем:
Получаем: 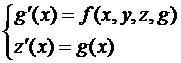
А. Модель радиоактивного распада. Основная идея модели. Основной недостаток модели. Как использовать модель для прогноза?
Пусть на какой-то территории выпало какое-то количество тонн радия. Какое количество радия распадётся за первые 100 лет?
Решение: пусть x – количество выпавшего радия, t – время, x(t) – скорость распада радия. При t=0, х(0)=х0.
Найдём скорость распада радия: 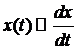 Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).
Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).
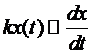 , где k – постоянно.
, где k – постоянно. 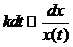 ->
-> 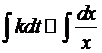 Решив эти интегралы, получаем:
Решив эти интегралы, получаем:
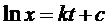 .
.
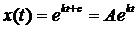 -первоначальная модель решения, но у нас нет А и k.
-первоначальная модель решения, но у нас нет А и k.
Находим их: 1. 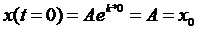 ->
->  .
.
2. 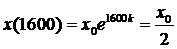 ->
-> 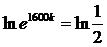 ->
->  ->
-> 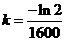 .
.
Итак, модель выглядит так:
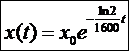 . Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.
. Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.
Идея модели dx/dt = x




 .
.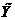 .
.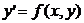 (1)
(1) где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).
где С – произвольная постоянная. Геометрически - это семейство интегральных кривых, каждая из которых является графиком решения (1) (рис.).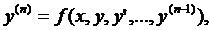 Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.
Задача Коши - задача нахождения частного решения уравнения, соответствующего начальным условиям y(x0)=y0.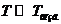
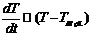 ,
, 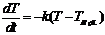 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const. => Проинтегрируем:
=> Проинтегрируем: 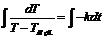 . Решив интегралы, получаем:
. Решив интегралы, получаем: 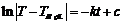 =>
=> 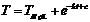 .
.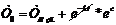 , где
, где 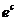 - В. В= Т0-Т возд =>
- В. В= Т0-Т возд => 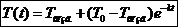 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня. Идея метода заключается в том, что на малом промежутке изменения независимой переменной
Идея метода заключается в том, что на малом промежутке изменения независимой переменной 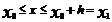 (где h – шаг таблицы) интегральная кривая диф-ного уравнения
(где h – шаг таблицы) интегральная кривая диф-ного уравнения  заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 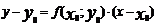 . Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Геометрически интегральная кривая заменяется при этом ломанной, называемой ломанной Эйлера.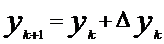 , где
, где 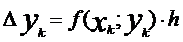 ,
, 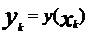 ,
, 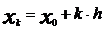
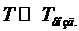
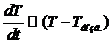 ,
, 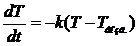 , где Т-Т возд. >0, а k-const.
, где Т-Т возд. >0, а k-const.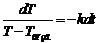 => Проинтегрируем:
=> Проинтегрируем: 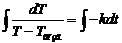 . Решив интегралы, получаем:
. Решив интегралы, получаем: 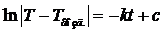 =>
=>  .
.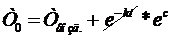 , где
, где 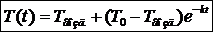 , где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.
, где Т0 – температура камня в начальный момент. Получили модель остывания нагретого камня.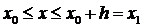 интегральная кривая дифференциального уравнения
интегральная кривая дифференциального уравнения 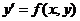 заменяется отрезком прямой (касательной)
заменяется отрезком прямой (касательной) 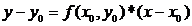 . Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.
. Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера.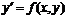 с начальными условиями
с начальными условиями 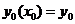 . Выберем шаг h и для кратности введем обозначения
. Выберем шаг h и для кратности введем обозначения  ,
, 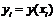 ,
, 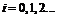 .
.
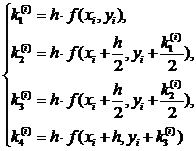
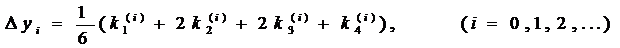 Последовательные приближения yi искомой функции y определяются по формуле:
Последовательные приближения yi искомой функции y определяются по формуле: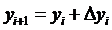 где (5)
где (5)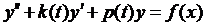 , где
, где 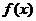 - вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
- вынуждающая функция, k – коэффициент трения, p – коэф. Пр.: Модель «хищник-жертва» Пусть Х – хищники, Y - жертвы. Тогда число хищников будет расти до тех пор, пока у них будет достаточно пищи, т.е. жертв, но в конце концов наступит такая ситуация, когда корма не будет хватать и в результате число хищников начнёт уменьшаться. Это приведёт к тому, что с некоторого момента число жертв начнёт увеличиваться. Это будет способствовать новому росту числа хищников, и цикл снова повторится. Определяем основные факторы, влияющие на воспроизводство хищников и жертв:
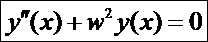 , где w-собственная частота гармонического осциллятора. Уравнение вида
, где w-собственная частота гармонического осциллятора. Уравнение вида 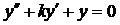 - математический маятник с трением, где k – коэф. трения. Уравнение вида
- математический маятник с трением, где k – коэф. трения. Уравнение вида 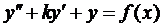 - с вынуждающей функцией.
- с вынуждающей функцией.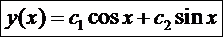 , с1, с2 – постоянные интегрирования. Пр.: При
, с1, с2 – постоянные интегрирования. Пр.: При 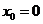 , ->
, ->  и
и  .
.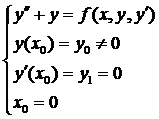
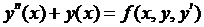 , где
, где 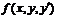 -трение маятника о воздух, или толчок маятника рукой. Пусть
-трение маятника о воздух, или толчок маятника рукой. Пусть  , тогда
, тогда 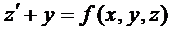 .
.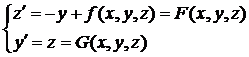

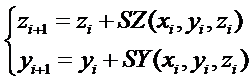
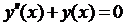 . Обозначим
. Обозначим 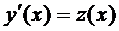 , тогда
, тогда 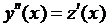 . Подставим:
. Подставим: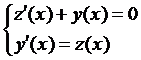
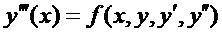 Обозначим:
Обозначим: 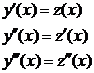
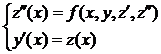
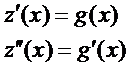 Получаем:
Получаем: 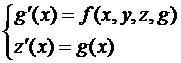
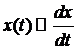 Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).
Скорость полураспада радия = 1600 лет. -> х(1600)=х(0)/2. Найти х(100).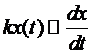 , где k – постоянно.
, где k – постоянно. 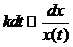 ->
-> 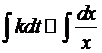 Решив эти интегралы, получаем:
Решив эти интегралы, получаем: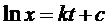 .
.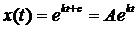 -первоначальная модель решения, но у нас нет А и k.
-первоначальная модель решения, но у нас нет А и k.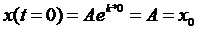 ->
->  .
.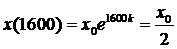 ->
-> 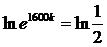 ->
->  ->
-> 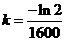 .
.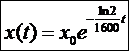 . Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.
. Теперь можем прогнозировать. Через 100 лет распадётся всего лишь 4,2% радиоактивного радия.


