Ядро и образ линейного оператора.
Определение. Множество 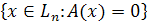 называется ядром линейного оператора и обозначается kerA
называется ядром линейного оператора и обозначается kerA
Определение. Множество векторов 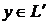 , являющихся значениями этого оператора называется образом линейного оператора и обозначается imA
, являющихся значениями этого оператора называется образом линейного оператора и обозначается imA
Размерность образа линейного оператора называется рангом 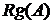 , а размерность ядра- дефектом линейного оператора
, а размерность ядра- дефектом линейного оператора 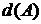 .
.
Теорема. Ядро линейного оператора A переводимого L→ 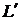 является подпространством в L, а его образ подпространством
является подпространством в L, а его образ подпространством 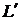 .
.
Теорема: «О размерности ядра и образа».
Если L – конечномерное пространство, то dim ker A+ dim im A= dimLZ
Матрица линейного оператора.
Рассмотрим линейный оператор A из пространства 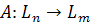 , где
, где 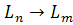 – линейные векторные пространства размерности n и m над общим полем P.
– линейные векторные пространства размерности n и m над общим полем P.
Фиксируем какой-нибудь базис, 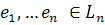 в пространстве
в пространстве 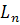 и базис
и базис 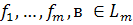
В силу линейности оператора A:
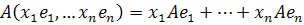 , поэтому A полностью определяется своим действием над базисными векторами
, поэтому A полностью определяется своим действием над базисными векторами  .
.
Разложим образы базисных векторов по базису пространства образа, т.е. базисные векторы пространства 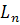 по базису
по базису 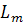
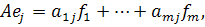 где j=1,
где j=1, 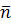 (от 1 до n)
(от 1 до n) 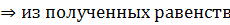
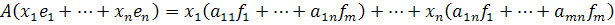
⇒ равенство в матричной форме:
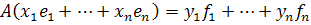
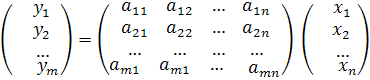
Матрица возникшая справа, называется матрицей линейного оператора А в паре базисов 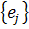 и
и 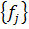
Матрица, составленная из координатных столбцов векторов 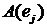 ,называется матрицей линейного оператора.
,называется матрицей линейного оператора.
Пример: Пусть A: L → 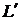 – оператор дифференцирования на пространстве многочленов степени < или =2.
– оператор дифференцирования на пространстве многочленов степени < или =2.
Рассмотрим 2 базиса:
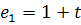 ,
,
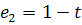 ,
,
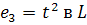
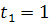
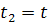
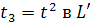
Очевидно: A(1+t) = 1
A(t-1) = -1
A(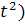 =2t
=2t
Поэтому в паре базисов 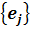 и
и 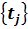 матрица линейного оператора имеет вид:
матрица линейного оператора имеет вид:
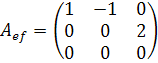
Какой будет матрица того же оператора, если L’=L и выбрать базис 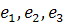
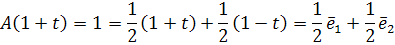
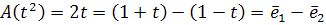
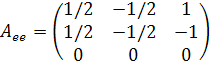
Теорема. Пусть 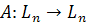 - линейный оператор. Тогда столбец y координат вектора
- линейный оператор. Тогда столбец y координат вектора 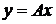 в данном базисе линейного пространства L равен произведению матрицы Аэтого оператора на столбец x координат вектора x в том же базисе.
в данном базисе линейного пространства L равен произведению матрицы Аэтого оператора на столбец x координат вектора x в том же базисе.
Переход к другим базисам.
Пусть 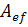 - матрица оператора A. Найдем матрицу
- матрица оператора A. Найдем матрицу 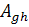 , того же оператора к другой паре базисов. Рассмотрим равенства:
, того же оператора к другой паре базисов. Рассмотрим равенства:
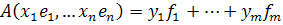
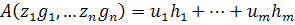
Согласно определению матрицы 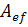 и
и 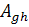 находим:
находим:
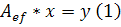
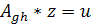
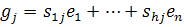
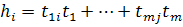
Найдем матрицы перехода:
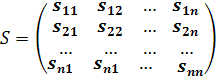
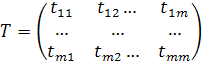
⇒x=Sz
y=Tu (2)
⇒ 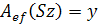
⇒ 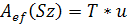
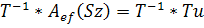
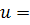 (
(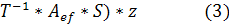
⇒ 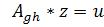
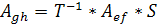
Напомним определение эквивалентных матриц (A и B называются эквивалентными, если B=P*A*Q, для P и Q – какие-то невырожденные матрицы.
Утверждение: - матрицы эквиваленты в том, и только в том случае, когда они являются матрицами одного и того же линейного оператора в каких то парах базиса.
Для того, чтобы матрицы одинаковых размеров были матрицами одного и того же линейного оператора, необходимо и достаточно, чтобы они имели одинаковый ранг.
Обратный оператор.
Оператор A из L→ 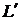 называется обратным, если существует оператор B:
называется обратным, если существует оператор B: 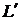 →L, такой что A(B(y))=y, ∀y ∈
→L, такой что A(B(y))=y, ∀y ∈ 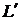 ; B(A(x))=x, ∀x∈L, при этом B называется обратным оператором для A.
; B(A(x))=x, ∀x∈L, при этом B называется обратным оператором для A.
Если линейный оператор обратим, то обратный оператор так же линейный.
Теорема. Пусть A:L→ 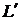 , линейный оператор, а L и
, линейный оператор, а L и 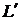 – конечномерные пространства одинаковой размерности, то А является обратимым оператором, тогда и только тогда, когда ядро оператора А состоит из нулевого вектора: kerA ={0}
– конечномерные пространства одинаковой размерности, то А является обратимым оператором, тогда и только тогда, когда ядро оператора А состоит из нулевого вектора: kerA ={0}
Замечание. Если линейный оператор A: L→ 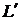 , обратим, то обязательно множество
, обратим, то обязательно множество 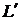 является образом оператора А
является образом оператора А 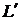 = imA
= imA
Замечание. В тоже время условие 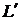 , равное образу А (
, равное образу А (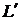 = imA) не всегда говорят о том, что оператор А обратим.
= imA) не всегда говорят о том, что оператор А обратим.
Если не вырожденный линейный оператор А пространства L в некотором базисе задается матрицей А (так же не вырождена), то обратный оператор задается в этом же базисе матрицей 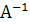 .
.
Ортогональные матрицы.
Пусть имеется евклидово n-мерное пространство 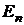 .
.
Определение. Матрица ортонормированной системы векторов 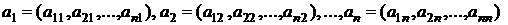 называется ортогональной. Для таких ортонормированных векторов имеем
называется ортогональной. Для таких ортонормированных векторов имеем
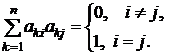
Единичные матрицы ортогональны. Например, ортогональными являются следующие единичные матрицы:
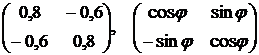 .
.
Теорема. Для того чтобы матрица А была ортогональной, необходимо и достаточно, чтобы выполнялось равенство 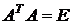 .
.
□ Если обозначить 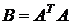 , то элементы этой матрицы будут равны
, то элементы этой матрицы будут равны 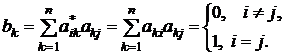
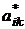 элементы транспонированной матрицы. Но это означает, что
элементы транспонированной матрицы. Но это означает, что 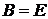 или
или 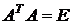 . И обратно, если
. И обратно, если 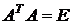 , имеем равенство
, имеем равенство
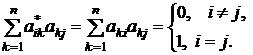
Что означает ортогональность матрицы А. ■
Следствия.
1. Модуль определителя ортогональной матрицы равен1.
2. Ортогональная матрица – невырожденная.
3. Произведение двух ортогональных матриц – ортогональная матрица.
4. Необходимым и достаточным условием ортогональности матрицы А является 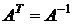 .
.
5. При транспонировании ортогональной матрицы получается ортогональная матрица.
6. Матрица, обратная ортогональной, тоже ортогональна.
Но сумма ортогональных матриц не является ортогональной.
Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.
Определение. Ортогональный оператор – это оператор евклидова пространства, матрица которого ортогональна в некотором ортонормированном базисе.
Теорема. Линейный оператор евклидова пространства является ортогональным тогда и только тогда, когда оно переводит ортонормированный базис в ортонормированный.
□ По предыдущей теореме матрица перехода от одного ортонормированного базиса к другому является ортогональной, следовательно, линейный оператор, соответствующий данной матрицы, ортогонален. И обратно, если имеется линейный оператор в некотором ортонормированном базисе с ортогональной матрицей, то из ортогональности следует, что
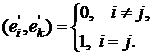
Где каждый из векторов второго базиса 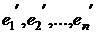 равен
равен 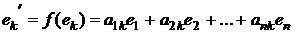 (
(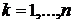 ), коэффициенты этого разложения составляют k-ый столбец ортогональной матрицы перехода. Отсюда следует ортонормированность базиса
), коэффициенты этого разложения составляют k-ый столбец ортогональной матрицы перехода. Отсюда следует ортонормированность базиса 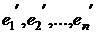 . ■
. ■
Известно, что ортогональный оператор не меняет скалярного произведения векторов (следует из выражения скалярного произведения через координаты векторов в ортонормированном базисе), а следовательно, не меняется норма вектора и угол между двумя векторами.
Ядро и образ линейного оператора.
Определение. Множество 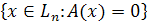 называется ядром линейного оператора и обозначается kerA
называется ядром линейного оператора и обозначается kerA
Определение. Множество векторов 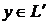 , являющихся значениями этого оператора называется образом линейного оператора и обозначается imA
, являющихся значениями этого оператора называется образом линейного оператора и обозначается imA
Размерность образа линейного оператора называется рангом 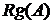 , а размерность ядра- дефектом линейного оператора
, а размерность ядра- дефектом линейного оператора 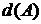 .
.
Теорема. Ядро линейного оператора A переводимого L→ 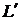 является подпространством в L, а его образ подпространством
является подпространством в L, а его образ подпространством 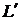 .
.
Теорема: «О размерности ядра и образа».
Если L – конечномерное пространство, то dim ker A+ dim im A= dimLZ



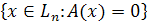 называется ядром линейного оператора и обозначается kerA
называется ядром линейного оператора и обозначается kerA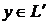 , являющихся значениями этого оператора называется образом линейного оператора и обозначается imA
, являющихся значениями этого оператора называется образом линейного оператора и обозначается imA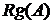 , а размерность ядра- дефектом линейного оператора
, а размерность ядра- дефектом линейного оператора 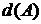 .
.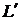 является подпространством в L, а его образ подпространством
является подпространством в L, а его образ подпространством 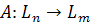 , где
, где 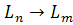 – линейные векторные пространства размерности n и m над общим полем P.
– линейные векторные пространства размерности n и m над общим полем P.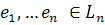 в пространстве
в пространстве 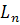 и базис
и базис 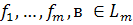
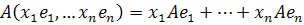 , поэтому A полностью определяется своим действием над базисными векторами
, поэтому A полностью определяется своим действием над базисными векторами  .
.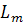
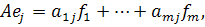 где j=1,
где j=1, 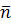 (от 1 до n)
(от 1 до n) 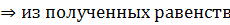
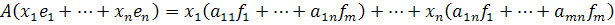
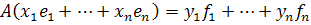
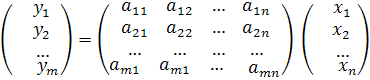
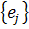 и
и 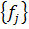
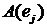 ,называется матрицей линейного оператора.
,называется матрицей линейного оператора.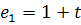 ,
, 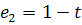 ,
, 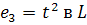
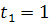
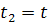
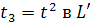
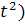 =2t
=2t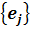 и
и 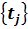 матрица линейного оператора имеет вид:
матрица линейного оператора имеет вид: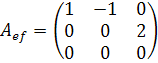
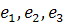
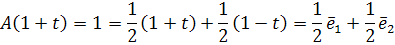
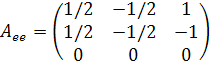
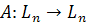 - линейный оператор. Тогда столбец y координат вектора
- линейный оператор. Тогда столбец y координат вектора 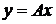 в данном базисе линейного пространства L равен произведению матрицы Аэтого оператора на столбец x координат вектора x в том же базисе.
в данном базисе линейного пространства L равен произведению матрицы Аэтого оператора на столбец x координат вектора x в том же базисе.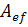 - матрица оператора A. Найдем матрицу
- матрица оператора A. Найдем матрицу 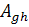 , того же оператора к другой паре базисов. Рассмотрим равенства:
, того же оператора к другой паре базисов. Рассмотрим равенства: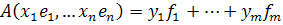
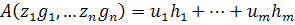
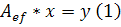
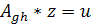
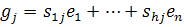
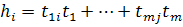
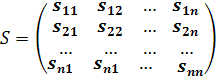
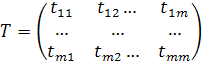
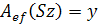
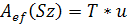
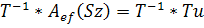
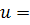 (
(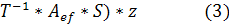
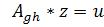
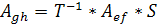
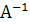 .
.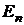 .
.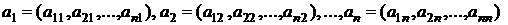 называется ортогональной. Для таких ортонормированных векторов имеем
называется ортогональной. Для таких ортонормированных векторов имеем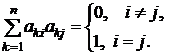
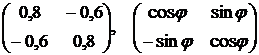 .
.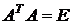 .
.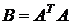 , то элементы этой матрицы будут равны
, то элементы этой матрицы будут равны 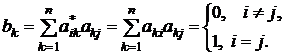
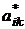 элементы транспонированной матрицы. Но это означает, что
элементы транспонированной матрицы. Но это означает, что 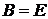 или
или 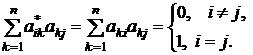
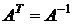 .
.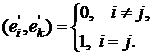
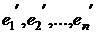 равен
равен 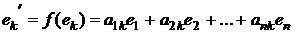 (
(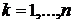 ), коэффициенты этого разложения составляют k-ый столбец ортогональной матрицы перехода. Отсюда следует ортонормированность базиса
), коэффициенты этого разложения составляют k-ый столбец ортогональной матрицы перехода. Отсюда следует ортонормированность базиса 

