Задание 1.
1. Вычислить предел 
 . Наберите:
. Наберите:
> Limit((1-x)*tan(Pi*x/2),x=1)=
limit((1-x)*tan(Pi*x/2),x=1);

2. Найти односторонние пределы 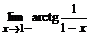 и
и  . Наберите:
. Наберите:
> Limit(arctan(1/(1-x)),x=1,left)=
limit(arctan(1/(1-x)), x=1, left);

> Limit(arctan(1/(1-x)),x=1,right)=
limit(arctan(1/(1-x)),x=1, right);
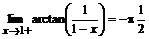
Дифференцирование
Вычисление производных.
Для вычисления производных в Maple имеются две команды:
1) прямого исполнения – diff(f,x), где f – функция, которую следует продифференцировать, x – имя переменной, по которой производится дифференцирование.
2) отложенного исполнения – Diff(f,x), где параметры команды такие же, как и в предыдущей. Действие этой команды сводится к аналитической записи производной в виде  . После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде вам нужен результат.
. После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде вам нужен результат.
Пример:
> Diff(sin(x^2),x)=diff(sin(x^2),x);

Для вычисления производных старших порядков следует указать в параметрах x$n, где n – порядок производной; например:
> Diff(cos(2*x)^2,x$4)=diff(cos(2*x)^2,x$4);

Полученное выражение можно упростить двумя способами:
> simplify(%);

> combine(%);

Дифференциальный оператор.
Для определения дифференциального оператора используется команда D(f) – f -функция. Например:
> D(sin);
cos
Вычисление производной в точке:
> D(sin)(Pi):eval(%);
-1
Оператор дифференцирования применяется к функциональным операторам
> f:=x-> ln(x^2)+exp(3*x):
> D(f);

Задание 2.
1. Вычислить производную 
> Diff(sin(2*x)^3-cos(2*x)^3,x)=
diff(sin(2*x)^3-cos(2*x)^3,x);

2. Вычислить 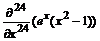 . Наберите:
. Наберите:
> Diff(exp(x)*(x^2-1),x$24)=
diff(exp(x)*(x^2-1),x$24):
> collect(%,exp(x));

3. Вычислить вторую производную функции  в точках x =p/2, x =p.
в точках x =p/2, x =p.
> y:=sin(x)^2/(2+sin(x)): d2:=diff(y,x$2):
> x:=Pi; d2y(x)=d2;
x:=p d2y(p)=1
> x:=Pi/2;d2y(x)=d2;
х:= 
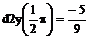
§3. Исследование функции
Исследование функции необходимо начинать с нахождения ее области определения, но, к сожалению, это трудно автоматизируемая операция. Поэтому при рассмотрении этого вопроса приходится решать неравенства (см. тему II). Однако, ответить на вопрос, определена ли функция на всей числовой оси, или нет, можно исследовав ее на непрерывность.
Задание 3.1.
1. Найдите точки разрыва функции 
> readlib(iscont): readlib(discont):
> iscont(exp(1/(x+3)),x=-infinity..+infinity);
false
Это означает, что функция не является непрерывной. Поэтому следует найти точки разрыва с помощью команды:
> discont(exp(1/(x+3)),x);
{-3}
Ответ наберите в текстовом режиме в новой строке:
“Точка разрыва x =-3.”
2. Найти точки разрыва функции 
> readlib(singular):
> iscont(tan(x/(2-x)),x=-infinity..infinity);
false
> singular(tan(x/(2-x)),x);
{ x =2},{ x =2  }
}
Здесь _ N – целые числа. Ответ наберите в текстовом режиме в новой строке:
“Точки разрыва: x =2 и x =2p(2 n +1)/(p(2 n +1)-2).”
Задание 3.2.
1. Найти max и min  .
.
> readlib(extrema):
> y:=(x^2-1/2)*arcsin(x)/2+x*sqrt(1-x^2)/4-
Pi*x^2/12:
> extrema(y,{},x,'s');s;


После выполнения этих команд найдены экстремумы функции и точки экстремумов. Порядок следования x –координат экстремумов во второй строке вывода соответствует порядку следования значений экстремумов в первой строке вывода. Таким образом, найдены экстремумы в точках (0,0) и (1/2, –p/24+  ). Осталось выяснить, какая из них является максимумом, а какая – минимумом. Для этого используйте команды maximize и minimize.
). Осталось выяснить, какая из них является максимумом, а какая – минимумом. Для этого используйте команды maximize и minimize.
> readlib(maximize):readlib(minimize):
> ymax:=maximize(y,{x});

> ymin:=minimize(y,{x});

Ответ наберите в текстовом режиме в новой строке:
“Экстремумы: 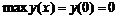 ,
,  .”
.”
 Для набора математических символов и греческих букв в текстовом режиме следует нажать кнопку со значком суммы на Панели инструментов. В появившейся строке ввода формул ниже Панели инструментов следует набирать обычные команды Maple,после чего нажать Enter. Например, для отображения формулы
Для набора математических символов и греческих букв в текстовом режиме следует нажать кнопку со значком суммы на Панели инструментов. В появившейся строке ввода формул ниже Панели инструментов следует набирать обычные команды Maple,после чего нажать Enter. Например, для отображения формулы 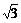 следует набрать в строке ввода формул sqrt(3).
следует набрать в строке ввода формул sqrt(3).
 Для возвращения в текстовый режим снова следует нажать на кнопку с буквой «Т».
Для возвращения в текстовый режим снова следует нажать на кнопку с буквой «Т».
Поэтому порядок набора второй формулы в ответе такой:
§ находясь в текстовом режиме, набрать: miny(x)=y(1/2)=;
§  нажать на кнопку
нажать на кнопку
§ в строке ввода формул набрать: -Pi/24+sqrt(3)/16
§ нажать Enter;

§ вернуться в текстовый режим.
2. Найдите наибольшее и наименьшее значение  на интервале
на интервале  . Наберите:
. Наберите:
> f:=x^2*ln(x):
> maximize(f,{x},{x=1..2});

> minimize(f,{x},{x=1..2}):simplify(%);
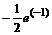
Ответ наберите в текстовом режиме в новой строке:
”Наибольшее значение:  , наименьшее значение
, наименьшее значение  “.
“.
3. Найти экстремумы функции  и установить их характер с помощью второй производной. Наберите:
и установить их характер с помощью второй производной. Наберите:
> restart:y:=x^3/(4-x^2): readlib(extrema):
readlib(maximize): readlib(minimize):
> extrema(y,{},x,'s');s;
{  }
}
{{ x =0},{  },{
},{  }}
}}
Получено два экстремума и три критические точки. Исследование можно продолжить с помощью второй производной:
> d2:=diff(y,x$2): x:=0: d2y(x):=d2;
d2y(0):=0
> x:=2*sqrt(3):d2y(x):=d2;

> x:=-2*sqrt(3):d2y(x):=d2;

Так как  , то в точке x =0 нет экстремума; так как
, то в точке x =0 нет экстремума; так как 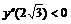 , то в точке
, то в точке  будет max; так как
будет max; так как  , то в точке
, то в точке  будет min. Перейдите в текстовый режим и запишите ответ в виде:
будет min. Перейдите в текстовый режим и запишите ответ в виде:
“Максимум в точке ( ), минимум в точке (
), минимум в точке (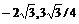 )”.
)”.
Построение графика.
Построение графика функции f (x)– это окончательный этап исследования функции. На рисунке помимо графика исследуемой функции f (x) должны быть нанесены все ее асимптоты пунктирными линиями, подписаны координаты точек max и min. Приемы построения графиков нескольких функций и нанесения надписей были рассмотрены в теме III.
Задание 3.3.
1. Провести полное исследование функции  по общей схеме. Сначала перейдите в текстовый режим и наберите “Исследование функции: “. Затем вернитесь в режим командной строки и наберите команды:
по общей схеме. Сначала перейдите в текстовый режим и наберите “Исследование функции: “. Затем вернитесь в режим командной строки и наберите команды:
> f:=x^4/(1+x)^3:
В текстовом режиме наберите “Непрерывность функции”. В режиме командной строки и наберите:
> readlib(iscont): readlib(discont):
readlib(singular):
> iscont(f, x=-infinity..infinity);
false
Это означает, что функция не является непрерывной. Перейдите в текстовый режим и наберите “Нахождение точек разрыва”. Вернитесь в режим командной строки и наберите:
> discont(f,x);
{-1}
Конвертировать полученное значение точки разрыва типа set в число можно командой convert, добавив вторую опцию, например, `+`. Обратите внимание на обратные кавычки, которые набираются клавишей, расположенной выше клавиши табуляции.
> xr:=convert(%,`+`);
xr:= -1
Перейдите в текстовый режим и наберите: “Получена точка бесконечного разрыва x =-1”. С новой строки наберите: “Нахождение асимптот.”. Перейдите на новую строку и наберите “Уравнение вертикальной асимптоты: x =-1” (это можно сделать, поскольку вертикальные асимптоты возникают в точках бесконечного разрыва). С новой строки наберите: “Коэффициенты наклонной асимптоты:”. Перейдите в режим командной строки и наберите:
> k1:=limit(f/x, x=+infinity);
k1:=1
> b1:=limit(f-k1*x, x=+infinity);
b1:= -3
> k2:=limit(f/x, x=-infinity);
k2:=1
> b2:=limit(f-k2*x, x=-infinity);
b2:= -3
В этом случае коэффициенты наклонных асимптот при  и
и 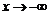 оказались одинаковыми. Поэтому перейдите в текстовый режим и наберите “Уравнение наклонной асимптоты:”. Затем в новой строке прейдите в режим командной строки и наберите:
оказались одинаковыми. Поэтому перейдите в текстовый режим и наберите “Уравнение наклонной асимптоты:”. Затем в новой строке прейдите в режим командной строки и наберите:
> y=k1*x+b1;

В текстовом режиме наберите “Нахождение экстремумов”. В новой строке наберите команды:
> readlib(extrema): readlib(maximize):
readlib(minimize):
> extrema(f,{},x,'s');s;
{  , 0}
, 0}
{{ x = -4},{ x =0}}
Поскольку функция имеет разрыв, то при поиске максимума и минимума следует указать интервал, в который не должна входить точка разрыва.
> fmax:=maximize(f,{x},{x=-infinity..-2});

> fmin:=minimize(f,{x},{x=-1/2..infinity});

В текстовом режиме наберите результат исследования в виде:
“Максимум в точке (-4, -256/27); минимум в точке (0, 0).”
2. Построить график функции 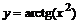 и ее асимптоту, указать координаты точек экстремума. Оформление каждого этапа исследования функции проделать также как и при выполнении предыдущего задания. Самостоятельно загрузите из стандартной библиотеки все необходимые команды.
и ее асимптоту, указать координаты точек экстремума. Оформление каждого этапа исследования функции проделать также как и при выполнении предыдущего задания. Самостоятельно загрузите из стандартной библиотеки все необходимые команды.
> restart: y:=arctan(x^2):
> iscont(y, x=-infinity..infinity);
true
> k1:=limit(y/x, x=-infinity);
k1:=0
> k2:=limit(y/x, x=+infinity);
k2:=0
> b1:=limit(y-k1*x, x=-infinity);

> b2:=limit(y-k1*x, x=+infinity);

> yh:=b1;

> extrema(y,{},x,'s');s;
{0}
{{ x =0}}
> ymax:=maximize(y,{x}); ymin:=minimize(y,{x});
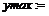
> with(plots): yy:=convert(y,string):
> p1:=plot(y,x=-5..5, linestyle=1, thickness=3,
color=BLACK):
> p2:=plot(yh,x=-5..5, linestyle=1,thickness=1):
> t1:=textplot([0.2,1.7,"Асимптота:"],
font=[TIMES, BOLD, 10], align=RIGHT):
> t2:=textplot([3.1,1.7,"y=Pi/2"],
font=[TIMES, ITALIC, 10], align=RIGHT):
> t3:=textplot([0.1,-0.2,"min:(0,0)"],
align=RIGHT):
> t4:=textplot([2,1,yy], font=[TIMES, ITALIC,
10], align=RIGHT):
> display([p1,p2,t1,t2,t3,t4]);

§4. Интегрирование
Задание 4.
1. Найти неопределенные интегралы: а)  ;
;
б)  .
.
> Int(cos(x)*cos(2*x)*cos(3*x),x)=
int(cos(x)*cos(2*x)*cos(3*x), x);
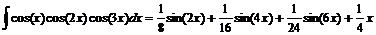
> Int((3*x^4+4)/(x^2*(x^2+1)^3),x)=
int((3*x^4+4)/(x^2*(x^2+1)^3),x);

2. Найти определенный интеграл  , при условии a >0, b >0.
, при условии a >0, b >0.
> assume (a>0); assume (b>0);
> Int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*sin(x)^2),
x=0..Pi/2)=int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*
sin(x)^2),x=0..Pi/2);

3. Найти несобственный интеграл 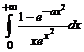 , при a >-1
, при a >-1
> restart; assume(a>-1);
> Int((1-exp(-a*x^2))/(x*exp(x^2)),
x=0..+infinity)=int((1-exp(-a*x^2))/(x*exp(x^2)),
x=0..+infinity);

4. Численно найти интеграл 
> Int(cos(x)/x, x=Pi/6..Pi/4)=evalf(int(cos(x)/x,
x=Pi/6..Pi/4), 15);

5. Полностью проделать все этапы вычисления интеграла  по частям.
по частям.
> restart; with(student): J=Int(x^3*sin(x),x);

> J=intparts(Int(x^3*sin(x),x),x^3);

> intparts(%,x^2);

> intparts(%,x);

> value(%);

6. Вычислить интеграл  с помощью универсальной подстановки
с помощью универсальной подстановки  .
.
> J=Int(1/(1+cos(x)), x=-Pi/2..Pi/2);

> J=changevar(tan(x/2)=t,Int(1/(1+cos(x)),
x=-Pi/2..Pi/2), t);

> value(%);
J =2
Контрольные задания.
1. Вычислите предел  .
.
2. Найти пределы функции  при
при 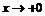 и при
и при 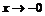 .
.
3. Найти  .
.
4. Найти точки разрыва функции  .
.
5. Найти экстремумы функции  ,
, 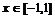 и указать их характер.
и указать их характер.
6. Провести полное исследование функции 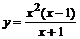 .
.
7. Построить график функции  с указанием координат экстремумов.
с указанием координат экстремумов.
8. Вычислить неопределенный интеграл  .
.
9. Вычислить несобственный интеграл  при a >0 b >0 для случаев a > b, a = b, a < b.
при a >0 b >0 для случаев a > b, a = b, a < b.
10. Численно найти интеграл  .
.
11. Полностью проделать все этапы вычисления интеграла  по частям.
по частям.
12. Вычислить интеграл 
 с помощью универсальной подстановки tg(x /2)= t.
с помощью универсальной подстановки tg(x /2)= t.
Контрольные вопросы.
1. Что такое команды прямого и отложенного исполнения? Опишите их действия.
2. С помощью какой команды вычисляются пределы? Какие у нее параметры?
3. Какие команды позволяют найти производную функции?
4. Опишите команды, позволяющие исследовать функцию на непрерывность.
5. Какая последовательность команд необходима для нахождения max и min функции с указанием их координат (x, y)?
6. Какие недостатки имеют команды maximize, minimize и extrema?
7. Опишите общую схему исследования функции и построение ее графика в Maple.
8. Какие команды производят аналитическое и численное интегрирование? Опишите их параметры.
9. С помощью каких команд вводятся ограничения на параметры для вычисления интегралов, зависящих от параметров?
10. Для чего предназначен пакет student?
11. Опишите команду интегрирования по частям.
12. Опишите команду интегрирования методом замены переменных.
V. Линейная алгебра
1. Векторная алгебра.
2. Действия с матрицами.
3. Спектральный анализ матрицы.
4. Системы линейных уравнений. Матричные уравнения.
§1. Векторная алгебра
Основная часть команд для решения задач линейной алгебры содержится в библиотеке linalg. Поэтому перед решением задач с матрицами и векторами следует загрузить эту библиотеку командой with(linalg).
Способы задания векторов.
Для определения вектора в Maple используется команда vector([x1,x2,…,xn]), где в квадратных скобках через запятую указываются координаты вектора. Например:
> x:=vector([1,0,0]);
x:=[1, 0, 0]
Координату уже определенного вектора x можно получить в строке вывода, если ввести команду x[i], где i - номер координаты. Например, первую координату заданного в предыдущем примере вектора можно вывести так:
> x[1];
Вектор можно преобразовать в список и, наоборот, с помощью команды convert(vector, list) или convert(list, vector).
Сложение векторов.
Сложить два вектора a и b можно с помощью двух команд:
1) evalm(a+b);
2) matadd(a,b).
Команда add позволяет вычислять линейную комбинацию векторов a и b:  , где
, где  - скалярные величины, если использовать формат: matadd(a,b,alpha,beta).
- скалярные величины, если использовать формат: matadd(a,b,alpha,beta).
Норма вектора.
Норму (длину) вектора 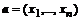 , которая равна
, которая равна  , можно вычислить с помощью команды norm(а,2).
, можно вычислить с помощью команды norm(а,2).
Можно нормировать вектор а с помощью команды normalize(a), в результате выполнения которой будет получен вектор единичной длины  .
.
Задание 1.
1. Даны два вектора:  и
и  . Найти
. Найти  и угол между a и b. Для решения этой задачи наберите:
и угол между a и b. Для решения этой задачи наберите:
> with(linalg):
> a:=([2,1,3,2]); b:=([1,2,-2,1]);
a:=[2,1,3,2]
b:=[1,2,-2,1]
> dotprod(a,b);
> phi=angle(a,b);

2. Найти векторное произведение  , а затем скалярное произведение
, а затем скалярное произведение 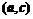 , где
, где  ,
,  .
.
> restart; with(linalg):
> a:=([2,-2,1]); b:=([2,3,6]);
a:=[2,-2,1]
b:=[2,3,6]
> c:=crossprod(a,b);
c:=[-15,-10,10]
> dotprod(a,c);
3. Найти норму вектора  .
.
> restart; with(linalg):
> a:=vector([1,2,3,4,5,6]): norm(a,2);

4. Из системы векторов:  ,
,  ,
,  ,
, 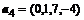 ,
, 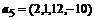 выделить базис и ортогонализовать его по процедуре Грамма-Шмидта:
выделить базис и ортогонализовать его по процедуре Грамма-Шмидта:
> restart; with(linalg):
> a1:=vector([1,2,2,-1]):
a2:=vector([1,1,-5,3]):
a3:=vector([3,2,8,7]): a4:=vector([0,1,7,-4]):
a5:=vector([2,1,12,-10]):
> g:=basis([a1,a2,a3,a4,a5]);
g:= [ a1, a2, a3, a5 ]
> GramSchmidt(g);
[[1,2,2,-1], [2,3,-3,2],  ,
, 
Действия с матрицами
Определение матрицы.
Для определения матрицы в Maple можно использовать команду matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…, [an1,an2,…,anm]]), где n - число строк, m – число столбцов в матрице. Эти числа задавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:
> A:=matrix([[1,2,3],[-3,-2,-1]]);

В Maple матрицы специального вида можно генерировать с помощью дополнительных команд. В частности диагональную матрицу можно получить командой diag. Например:
> J:=diag(1,2,3);

Генерировать матрицу можно с помощью функции f (i, j) от переменных i, j – индексов матрицы: matrix(n, m, f), где где n - число строк, m – число столбцов. Например:
> f:=(i, j)->x^i*y^j;

> A:=matrix(2,3,f);

Число строк в матрице А можно определить с помощью команды rowdim(A), а число столбцов – с помощью команды coldim(A).
Выяснение типа матрицы.
Выяснить положительную или отрицательную определенность матрицы можно при помощи команды definite(A,param), где param может принимать значения: 'positive_def' – положительно определена (A >0), 'positive_semidef' – неотрицательно определенная  , 'negative_def' – отрицательно определенная (A <0), 'negative_semidef' - неположительно определенная
, 'negative_def' – отрицательно определенная (A <0), 'negative_semidef' - неположительно определенная  . Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например:
. Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например:
> A:=matrix([[2,1],[1,3]]);
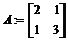
> definite(А,'positive_def');
true
Проверить ортогональность матрицы А можно командой orthog(A).
> В:=matrix([[1/2,1*sqrt(3)/2],
[1*sqrt(3)/2,-1/2]]);

> orthog(В);
true
Функции от матриц.
Возведение матрицы А в степень n производится командой evalm(A^n). Вычисление матричной экспоненты  возможно с помощью команды exponential(A). Например:
возможно с помощью команды exponential(A). Например:
> Т:=matrix([[5*a,2*b],[-2*b,5*a]]);

> exponential(Т);
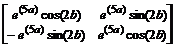
> evalm(Т^2);

Задание 2.
1. Даны матрицы: 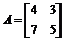 ,
, 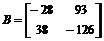 ,
,  . Найти: (AB) C, det A, det B, det C, det[(AB) C ]. Наберите:
. Найти: (AB) C, det A, det B, det C, det[(AB) C ]. Наберите:
> with(linalg):restart;
> A:=matrix([[4,3],[7,5]]):
> B:=matrix([[-28,93],[38,-126]]):
> C:=matrix([[7,3],[2,1]]):
> F:=evalm(A&*B&*C);

> Det(A)=det(A); Det(B)=det(B); Det(C)=det(C);
Det(F)=det(F);
Det(A)=-1
Det(B)=-6
Det(C)=1
Det(F)=6
2. Дана матрица 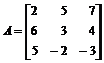 , найти: det A,
, найти: det A,  , A’, det(M 22). Наберите:
, A’, det(M 22). Наберите:
> A:=matrix([[2,5,7],[6,3,4],[5,-2,-3]]);

> Det(A)=det(A);
Det(A)=-1
> transpose(A);

> inverse(A);
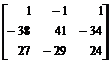
> det(minor(A,2,2));
-41
3. Найти ранг матрицы 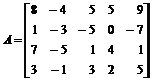 .
.
> A:=matrix([[8,-4,5,5,9], [1,-3,-5,0,-7],
[7,-5,1,4,1], [3,-1,3,2,5]]):
> r(A)=rank(A);
r(A)=3
4. Вычислить  , где
, где  .
.
> exponential([[3,-1],[1,1]]);

5. Дана матрица  . Найти значение многочлена
. Найти значение многочлена  .
.
> A:=matrix([[5,1,4],[3,3,2],[6,2,10]]):
> P(A)=evalm(A^3-18*A^2+64*A);
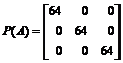
§3. Спектральный анализ матрицы
Задание 3.
1. Дана матрица  . Найти ее собственные векторы и собственные числа.
. Найти ее собственные векторы и собственные числа.
> U:=matrix([[3,2-I],[2+I,7]]):
> eigenvectors(U);
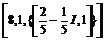 ,
, 
2. Дана матрица  . Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.
. Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.
> A:=matrix([[3,-I,0],[I,3,0],[0,0,4]]):
> eigenvectors(A);
[2, 1, {([1, - I, 0])}], [4, 2, {([0, 0, 1]), ([- I, 1, 0])}]
> P(lambda):=charpoly(A,lambda);

> d(lambda):=minpoly(A,lambda);

> jordan(A);

3. Дана матрица  . Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.
. Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.
> A:=matrix([[1,-3,4],[4,-7,8],[6,-7,7]]):
> j:=jordan(A);

> g:=gausselim(A);

> F(A):=charmat(A,lambda);

Самостоятельно проверьте, чем будет отличаться результат выполнения команды ffgausselim(A) от gausselim(A) на этом примере.
§4. Системы линейных уравнений. Матричные уравнения
Ядро матрицы.
Ядро матрицы А – это множество векторов х таких, произведение матрицы А на которые равно нулевому вектору:  . Поиск ядра матрицы А эквивалентен решению системы линейных однородных уравнений. Найти ядро матрицы А можно командой kernel(A).
. Поиск ядра матрицы А эквивалентен решению системы линейных однородных уравнений. Найти ядро матрицы А можно командой kernel(A).
Задание 4.
1. Найти общее и одно частное решение системы: 
> eq:={2*x-3*y+5*z+7*t=1, 4*x-6*y+2*z+3*t=2,
2*x-3*y-11*z-15*t=1}:
> s:=solve(eq,{x,y,z});
s:={  , y = y,
, y = y,  }
}
Для нахождения частного решения следует выполнить подстановку конкретного значения одной из переменных при помощи команды subs:
> subs({y=1,t=1},s);
{  ,
,  , 1=1}
, 1=1}
2. Решить матричное уравнение: АX = В; где  ,
, 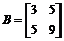
> A:=matrix([[1,2],[3,4]]):
> B:=matrix([[3,5],[5,9]]):
> X:=linsolve(A,B);
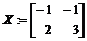
3. Дана матрица  . Найти ее ранг, дефект: d (A)= n – r (A), где n – размерность квадратной матрицы, r – ее ранг. Найти ядро А. Наберите:
. Найти ее ранг, дефект: d (A)= n – r (A), где n – размерность квадратной матрицы, r – ее ранг. Найти ядро А. Наберите:
> A:=matrix([[1,1,0],[0,2,-1],[1,3,-1]]):
> r(A):=rank(A);
r(A):=2
> d(A):=rowdim(A)-r(A);
d(A):=1
> k(A):=kernel(A);
k(A):={[-1,1,2]}
Контрольные задания.
1) Даны 2 вектора:  ,
, 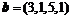 . Найти
. Найти  и угол j между этими векторами.
и угол j между этими векторами.
2) Даны 3 вектора: 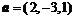 ,
,  и
и  . Найти:
. Найти: 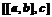 и
и  .
.
3) Даны системы векторов:  ,
,  ,
,  ,
,  . Предварительно выяснив, является ли система
. Предварительно выяснив, является ли система  базисом, применить процедуру ортогонализации Грамма-Шмидта и построить ортогональный базис этого подпространства.
базисом, применить процедуру ортогонализации Грамма-Шмидта и построить ортогональный базис этого подпространства.
4) Даны матрицы  и
и  . Найти: AB, BA, det A, det B.
. Найти: AB, BA, det A, det B.
5) Дана матрица:  . Найти: det A, А -1, M 32, A '.
. Найти: det A, А -1, M 32, A '.
6) Найти ранг матрицы:  . Привести матрицу С к треугольному виду.
. Привести матрицу С к треугольному виду.
7) Дана матрица  . Найти ее спектр, характеристический многочлен и значение матрицы на нем (вместо переменной l в PА (l) подставить А).
. Найти ее спектр, характеристический многочлен и значение матрицы на нем (вместо переменной l в PА (l) подставить А).
8) Дана матрица  . Найти
. Найти  , det(
, det( ), собственные векторы и собственные числа матрицы
), собственные векторы и собственные числа матрицы  , ядро матрицы Т.
, ядро матрицы Т.
9) Дана матрица  . Найти нормальную форму Жордана, собственные векторы и числа, найти характеристический и минимальный многочлены.
. Найти нормальную форму Жордана, собственные векторы и числа, найти характеристический и минимальный многочлены.
10) Решить матричное уравнение: АХ = В, где  ,
,  .
.
Контрольные вопросы.
1. Какой пакет следует загрузить перед решением задач линейной алгебры в Maple?
2. С помощью каких команд можно ввести вектор, матрицу?
3. Какими двумя командами можно сложить два вектора одинаковой размерности (2 матрицы)?
4. Какие виды произведений векторов вычисляются Maple и какие команды для этого используются?
5. Как вычислить норму вектора?
6. Как вычислить угол между двумя векторами?
7. Опишите команды нахождения базиса системы векторов и построение ортогонального базиса системы векторов.
8. Какими двумя командами можно вычислить произведение двух матриц (или матрицы на вектор)?
9. Какие команды используются для нахождения определителя, минора, алгебраического дополнения, следа матрицы?
10. Что такое дефект матрицы? Опишите способ нахождения дефекта квадратной матрицы. Какие команды при этом используются?
11. Какая матрица называется обратной и какими способами она вычисляется в Maple?
12. Что называется собственным вектором и собственным числом матрицы? Что называется спектром матрицы? Какие команды используются для нахождения спектра матрицы и ее собственных векторов? В каком виде в Maple выводятся результаты выполнения этих команд?
13. Перечислите специальные виды матриц и команды, приводящие матрицы к этим формам.
14. Что называется ядром матрицы, и какая команда используется для его нахождения?
15. Какая команда позволяет решать матричные уравнения?
Задание 1.
1. Вычислить предел 
 . Наберите:
. Наберите:
> Limit((1-x)*tan(Pi*x/2),x=1)=
limit((1-x)*tan(Pi*x/2),x=1);

2. Найти односторонние пределы 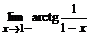 и
и  . Наберите:
. Наберите:
> Limit(arctan(1/(1-x)),x=1,left)=
limit(arctan(1/(1-x)), x=1, left);

> Limit(arctan(1/(1-x)),x=1,right)=
limit(arctan(1/(1-x)),x=1, right);
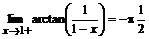
Дифференцирование
Вычисление производных.
Для вычисления производных в Maple имеются две команды:
1) прямого исполнения – diff(f,x), где f – функция, которую следует продифференцировать, x – имя переменной, по которой производится дифференцирование.
2) отложенного исполнения – Diff(f,x), где параметры команды такие же, как и в предыдущей. Действие этой команды сводится к аналитической записи производной в виде  . После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде вам нужен результат.
. После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде вам нужен результат.
Пример:
> Diff(sin(x^2),x)=diff(sin(x^2),x);

Для вычисления производных старших порядков следует указать в параметрах x$n, где n – порядок производной; например:
> Diff(cos(2*x)^2,x$4)=diff(cos(2*x)^2,x$4);

Полученное выражение можно упростить двумя способами:
> simplify(%);

> combine(%);

Дифференциальный оператор.
Для определения дифференциального оператора используется команда D(f) – f -функция. Например:
> D(sin);
cos
Вычисление производной в точке:
> D(sin)(Pi):eval(%);
-1
Оператор дифференцирования применяется к функциональным операторам
> f:=x-> ln(x^2)+exp(3*x):
> D(f);

Задание 2.
1. Вычислить производную 
> Diff(sin(2*x)^3-cos(2*x)^3,x)=
diff(sin(2*x)^3-cos(2*x)^3,x);

2. Вычислить 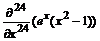 . Наберите:
. Наберите:
> Diff(exp(x)*(x^2-1),x$24)=
diff(exp(x)*(x^2-1),x$24):
> collect(%,exp(x));

3. Вычислить вторую производную функции 
|
|
|




 . Наберите:
. Наберите:
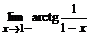 и
и  . Наберите:
. Наберите:
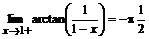
 . После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде вам нужен результат.
. После выполнения дифференцирования, полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде вам нужен результат.






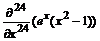 . Наберите:
. Наберите:
 в точках x =p/2, x =p.
в точках x =p/2, x =p.
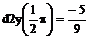


 }
} .
.

 ). Осталось выяснить, какая из них является максимумом, а какая – минимумом. Для этого используйте команды maximize и minimize.
). Осталось выяснить, какая из них является максимумом, а какая – минимумом. Для этого используйте команды maximize и minimize.

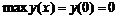 ,
,  .”
.” Для набора математических символов и греческих букв в текстовом режиме следует нажать кнопку со значком суммы на Панели инструментов. В появившейся строке ввода формул ниже Панели инструментов следует набирать обычные команды Maple,после чего нажать Enter. Например, для отображения формулы
Для набора математических символов и греческих букв в текстовом режиме следует нажать кнопку со значком суммы на Панели инструментов. В появившейся строке ввода формул ниже Панели инструментов следует набирать обычные команды Maple,после чего нажать Enter. Например, для отображения формулы 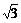 следует набрать в строке ввода формул sqrt(3).
следует набрать в строке ввода формул sqrt(3). Для возвращения в текстовый режим снова следует нажать на кнопку с буквой «Т».
Для возвращения в текстовый режим снова следует нажать на кнопку с буквой «Т». нажать на кнопку
нажать на кнопку
 на интервале
на интервале  . Наберите:
. Наберите:
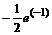
 , наименьшее значение
, наименьшее значение  “.
“. и установить их характер с помощью второй производной. Наберите:
и установить их характер с помощью второй производной. Наберите: }
} },{
},{  }}
}}

 , то в точке x =0 нет экстремума; так как
, то в точке x =0 нет экстремума; так как 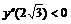 , то в точке
, то в точке  , то в точке
, то в точке  ), минимум в точке (
), минимум в точке (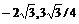 )”.
)”. по общей схеме. Сначала перейдите в текстовый режим и наберите “Исследование функции: “. Затем вернитесь в режим командной строки и наберите команды:
по общей схеме. Сначала перейдите в текстовый режим и наберите “Исследование функции: “. Затем вернитесь в режим командной строки и наберите команды: и
и 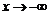 оказались одинаковыми. Поэтому перейдите в текстовый режим и наберите “Уравнение наклонной асимптоты:”. Затем в новой строке прейдите в режим командной строки и наберите:
оказались одинаковыми. Поэтому перейдите в текстовый режим и наберите “Уравнение наклонной асимптоты:”. Затем в новой строке прейдите в режим командной строки и наберите:
 , 0}
, 0}

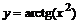 и ее асимптоту, указать координаты точек экстремума. Оформление каждого этапа исследования функции проделать также как и при выполнении предыдущего задания. Самостоятельно загрузите из стандартной библиотеки все необходимые команды.
и ее асимптоту, указать координаты точек экстремума. Оформление каждого этапа исследования функции проделать также как и при выполнении предыдущего задания. Самостоятельно загрузите из стандартной библиотеки все необходимые команды.


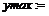
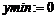

 ;
; .
.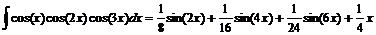

 , при условии a >0, b >0.
, при условии a >0, b >0.
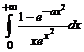 , при a >-1
, при a >-1


 по частям.
по частям.




 с помощью универсальной подстановки
с помощью универсальной подстановки  .
.

 .
. при
при 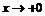 и при
и при 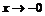 .
. .
. .
. ,
, 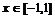 и указать их характер.
и указать их характер.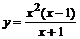 .
. с указанием координат экстремумов.
с указанием координат экстремумов. .
. при a >0 b >0 для случаев a > b, a = b, a < b.
при a >0 b >0 для случаев a > b, a = b, a < b. .
. по частям.
по частям.
 , где
, где  - скалярные величины, если использовать формат: matadd(a,b,alpha,beta).
- скалярные величины, если использовать формат: matadd(a,b,alpha,beta).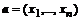 , которая равна
, которая равна  , можно вычислить с помощью команды norm(а,2).
, можно вычислить с помощью команды norm(а,2). .
. и
и  . Найти
. Найти  и угол между a и b. Для решения этой задачи наберите:
и угол между a и b. Для решения этой задачи наберите:
 , а затем скалярное произведение
, а затем скалярное произведение 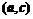 , где
, где  ,
,  .
.
 ,
,  ,
,  ,
, 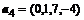 ,
, 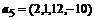 выделить базис и ортогонализовать его по процедуре Грамма-Шмидта:
выделить базис и ортогонализовать его по процедуре Грамма-Шмидта: ,
, 




 , 'negative_def' – отрицательно определенная (A <0), 'negative_semidef' - неположительно определенная
, 'negative_def' – отрицательно определенная (A <0), 'negative_semidef' - неположительно определенная  . Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например:
. Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например: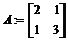

 возможно с помощью команды exponential(A). Например:
возможно с помощью команды exponential(A). Например:
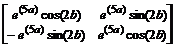

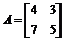 ,
, 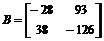 ,
,  . Найти: (AB) C, det A, det B, det C, det[(AB) C ]. Наберите:
. Найти: (AB) C, det A, det B, det C, det[(AB) C ]. Наберите:
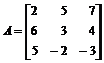 , найти: det A,
, найти: det A,  , A’, det(M 22). Наберите:
, A’, det(M 22). Наберите:

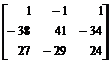
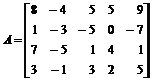 .
. , где
, где  .
.
 . Найти значение многочлена
. Найти значение многочлена  .
.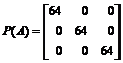
 . Найти ее собственные векторы и собственные числа.
. Найти ее собственные векторы и собственные числа.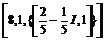 ,
, 
 . Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.
. Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.


 . Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.
. Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.


 . Поиск ядра матрицы А эквивалентен решению системы линейных однородных уравнений. Найти ядро матрицы А можно командой kernel(A).
. Поиск ядра матрицы А эквивалентен решению системы линейных однородных уравнений. Найти ядро матрицы А можно командой kernel(A).
 , y = y,
, y = y,  }
} ,
,  , 1=1}
, 1=1} ,
, 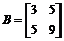
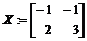
 . Найти ее ранг, дефект: d (A)= n – r (A), где n – размерность квадратной матрицы, r – ее ранг. Найти ядро А. Наберите:
. Найти ее ранг, дефект: d (A)= n – r (A), где n – размерность квадратной матрицы, r – ее ранг. Найти ядро А. Наберите: ,
, 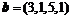 . Найти
. Найти 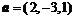 ,
,  и
и  . Найти:
. Найти: 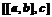 и
и  .
. ,
,  ,
,  ,
,  . Предварительно выяснив, является ли система
. Предварительно выяснив, является ли система  базисом, применить процедуру ортогонализации Грамма-Шмидта и построить ортогональный базис этого подпространства.
базисом, применить процедуру ортогонализации Грамма-Шмидта и построить ортогональный базис этого подпространства. и
и  . Найти: AB, BA, det A, det B.
. Найти: AB, BA, det A, det B. . Найти: det A, А -1, M 32, A '.
. Найти: det A, А -1, M 32, A '. . Привести матрицу С к треугольному виду.
. Привести матрицу С к треугольному виду. . Найти ее спектр, характеристический многочлен и значение матрицы на нем (вместо переменной l в PА (l) подставить А).
. Найти ее спектр, характеристический многочлен и значение матрицы на нем (вместо переменной l в PА (l) подставить А). . Найти
. Найти  . Найти нормальную форму Жордана, собственные векторы и числа, найти характеристический и минимальный многочлены.
. Найти нормальную форму Жордана, собственные векторы и числа, найти характеристический и минимальный многочлены. ,
,  .
.

