Рассчитать ферму – это значит определить усилия в ее стержнях. Этот метод состоит в том, что мысленно вырезают узлы фермы, рассматривая их равновесие. Действие отброшенной части фермы заменяют усилиями, возникающими в стержнях, которые попадают в разрез. Поэтому схема нагружения узла будет представлять систему сходящихся сил на плоскости, для которой можно составить только два уравнения равновесия.
Начинать расчет необходимо с нагруженного узла, в котором сходятся не более двух стержней.
Так как в начале расчета фермы неизвестно, какие стержни растянуты и какие сжаты, то условно предполагают, что все стержни растянуты и направляют усилия от узлов. Если в результате вычислений получается ответ со знаком минус, то соответствующий стержень сжат.
Дальнейшая последовательность рассмотрения узлов определяется так, чтобы число неизвестных сил, приложенных к узлу, не превышало двух.
Аналитические расчеты по определению величины и направления усилий в стержнях фермы проверяются графическими методами.
| Для этого строится силовой многоугольник всех известных и неизвестных сил, приложенных к узлу(рис. 18). Он должен быть замкнут.
Начнем расчет фермы с узла I.
1. Вычерчиваем схему нагружения узла I.
2. Составляем уравнение равновесия:
|
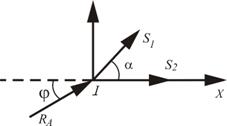 Рисунок 18 – Схема
нагружения узла I
Рисунок 18 – Схема
нагружения узла I
|
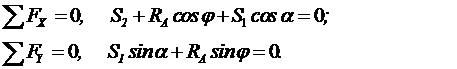
3. Определяем усилия в стержнях 1 и 2.
ü Из уравнения (12) имеем:
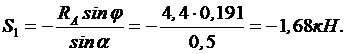
ü Из уравнения (11):
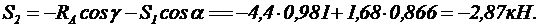
Значит, оба стержня сжаты.
| 4. Строим силовой многоугольник для узла I. Так как на узел I действуют только три силы, то многоугольником будет треугольник (рис. 19).
Выбираем масштаб сил:
| 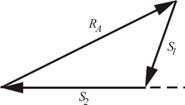 Рисунок 19 – Силовой
многоугольник узла I
Рисунок 19 – Силовой
многоугольник узла I
|
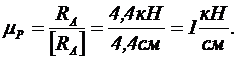
Следовательно, силу RА изображаем отрезком [ RА ]= 4,4 см. Из начала RА проводим линию, параллельную стержню 2, а из конца строим линию, параллельную стержню 1. Зная направление известной силы RА, замыкаем контур треугольника, из которого определяем величины усилий стержней 1 и 2:
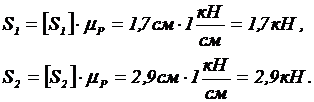
Так как усилия направлены к узлу (а это значит, что стержни сжаты), то усилия S1 и S2 должны быть со знаком «минус».
Теперь рассчитываем узел II.
1. Вычерчиваем схему нагружения узла II (рис. 20).
2. Составляем уравнение равновесия:
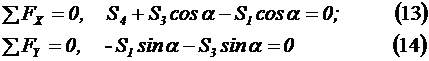
|
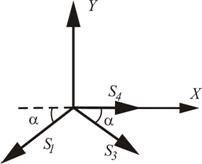 Рисунок 20 – Схема
нагружения узла II
Рисунок 20 – Схема
нагружения узла II
|
3. Определяем усилия в стержнях 3 и 4:
ü Из уравнения (14): 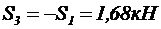 .
.
ü Из уравнения (13):
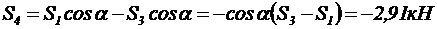
4. Строим силовой треугольник, из которого имеем (рис. 21):
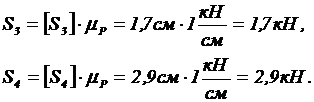
|
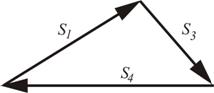 Рисунок 21 – Силовой
многоугольник узла II
Рисунок 21 – Силовой
многоугольник узла II
|
| Расчет узла III.
1. Вычерчиваем схему нагружения узла 3 (рис. 22).
|
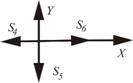 Рисунок 22 – Схема
нагружения узла III
Рисунок 22 – Схема
нагружения узла III
|
2. Составляем уравнения равновесия:
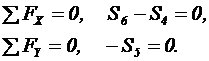
3. Определяем усилия в стержнях 5 и 6:
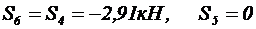 .
.
4. Строим силовой многоугольник, из которого имеем (рис. 23):
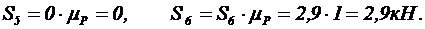
| 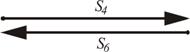 Рисунок 23 – Силовой многоугольник узла III
Рисунок 23 – Силовой многоугольник узла III
|
Расчет узла I V.
1. Вычерчиваем схему нагружения узла IV (рис. 24).
2. Составляем уравнения равновесия:
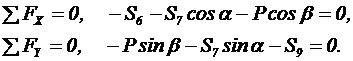
| 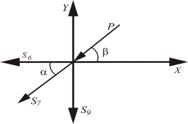 Рисунок 24 – Схема нагружения узла IV
Рисунок 24 – Схема нагружения узла IV
|
3. Определяем усилия в стержнях 7 и 9:
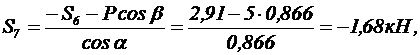
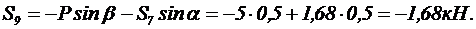
4. Строим силовой многоугольник, из которого имеем (рис. 25):
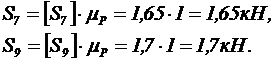
| 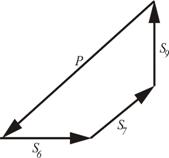 Рисунок 25 – Силовой
многоугольник узла IV
Рисунок 25 – Силовой
многоугольник узла IV
|
Расчет узла V.
1. Вычерчиваем схему нагружения узла V (рис. 26).
2. Составляем уравнения равновесия.
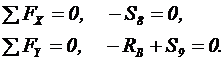 3. Определяем усилие в стержне 8:
3. Определяем усилие в стержне 8:
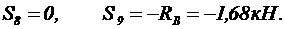 4. Строим силовой треугольник, из которого имеем (рис. 27):
4. Строим силовой треугольник, из которого имеем (рис. 27):
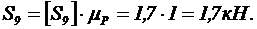
|
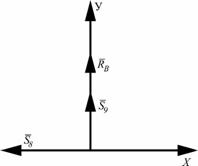 Рисунок 26 – Схема
нагружения узла V
Рисунок 26 – Схема
нагружения узла V
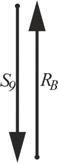 Рисунок 27 – Силовой
многоугольник узла V
Рисунок 27 – Силовой
многоугольник узла V
|
| | | |
Проверка
Для проверки необходимо рассматривать равновесие узла, в котором сходится наибольшее количество стержней. В данном примере это узел VI.
1. Вычерчиваем схему нагружения узла VI (рис. 28).
2. Составляем уравнения равновесия:
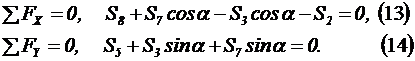
| 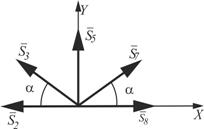 Рисунок 28 – Схема
нагружения узла VI
Рисунок 28 – Схема
нагружения узла VI
|
3. В уравнения (13), (14) подставляем значения усилий в стержнях фермы, полученных при расчете методом значения узлов. Если после подстановки получаем тождество 0=0, следовательно, задача решена правильно.
Итак: 0-1.68×0.866-1.68×0.866+2.87=0, 0=0,
0+1.68×0.5+0.5+(-1.68×0.5)=0, 0=0.



 Рисунок 18 – Схема
нагружения узла I
Рисунок 18 – Схема
нагружения узла I
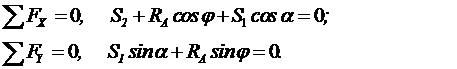
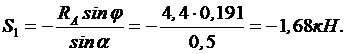
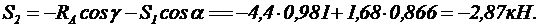
 Рисунок 19 – Силовой
многоугольник узла I
Рисунок 19 – Силовой
многоугольник узла I
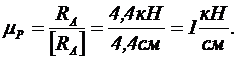
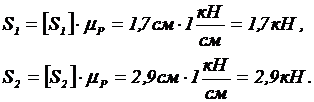
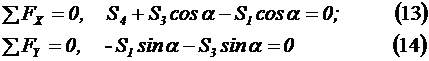
 Рисунок 20 – Схема
нагружения узла II
Рисунок 20 – Схема
нагружения узла II
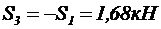 .
.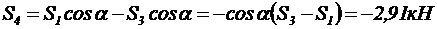
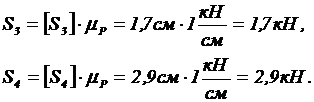
 Рисунок 21 – Силовой
многоугольник узла II
Рисунок 21 – Силовой
многоугольник узла II
 Рисунок 22 – Схема
нагружения узла III
Рисунок 22 – Схема
нагружения узла III
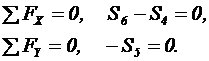
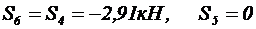 .
.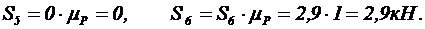
 Рисунок 23 – Силовой многоугольник узла III
Рисунок 23 – Силовой многоугольник узла III
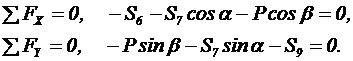
 Рисунок 24 – Схема нагружения узла IV
Рисунок 24 – Схема нагружения узла IV
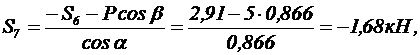
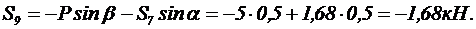
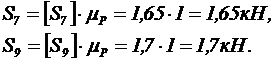
 Рисунок 25 – Силовой
многоугольник узла IV
Рисунок 25 – Силовой
многоугольник узла IV
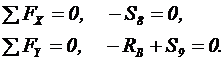 3. Определяем усилие в стержне 8:
3. Определяем усилие в стержне 8:
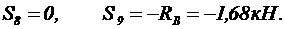 4. Строим силовой треугольник, из которого имеем (рис. 27):
4. Строим силовой треугольник, из которого имеем (рис. 27):
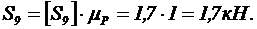
 Рисунок 26 – Схема
нагружения узла V
Рисунок 26 – Схема
нагружения узла V
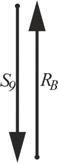 Рисунок 27 – Силовой
многоугольник узла V
Рисунок 27 – Силовой
многоугольник узла V
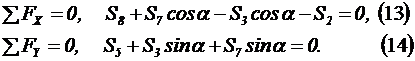
 Рисунок 28 – Схема
нагружения узла VI
Рисунок 28 – Схема
нагружения узла VI



