Учебное пособие по «Математическому анализу»
Составила Н.И.Макарчук
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения (Д.У.) занимают особое место в математике, имеют многочисленные применения.
Основной задачей теории Д.У. является изучение функций, представляющих собой решение этих уравнений. Если функция зависит от одной переменной, то Д.У. называются обыкновенными. Теория Д.У., когда неизвестные функции зависят от нескольких переменных, является более сложной и представляет специальный раздел математики – уравнения в частных производных.
Геометрический смысл дифференциального уравнения первого порядка.
Рассмотрим уравнение  . Пусть
. Пусть  его решение, график которого представляет собой непрерывную интегральную кривую, причем в каждой её точке существует касательная. Из записи дифференциального уравнения следует, что угловой коэффициент касательной к интегральной кривой в каждой её точке равен правой части этого уравнения. Следовательно, уравнение I-го порядка задает угловой коэффициент (
его решение, график которого представляет собой непрерывную интегральную кривую, причем в каждой её точке существует касательная. Из записи дифференциального уравнения следует, что угловой коэффициент касательной к интегральной кривой в каждой её точке равен правой части этого уравнения. Следовательно, уравнение I-го порядка задает угловой коэффициент ( )
)
касательной к интегральной кривой как функцию двух переменных. Если каждой точке  сопоставить отрезок направленный под углом наклона
сопоставить отрезок направленный под углом наклона  к оси
к оси 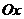 , то мы получим поле направлений данного уравнения. В этом заключается геометрический смысл дифференциального уравнения I-го порядка. Поле направлений позволяет проанализировать решение дифференциального уравнения и даже приближенно построить интегральные кривые.
, то мы получим поле направлений данного уравнения. В этом заключается геометрический смысл дифференциального уравнения I-го порядка. Поле направлений позволяет проанализировать решение дифференциального уравнения и даже приближенно построить интегральные кривые.
Пример1. Составить дифференциальное уравнение семейства окружностей  .
.
Решение.  ,
,


 .
.
 . Это и есть дифференциальное уравнение семейства окружностей.
. Это и есть дифференциальное уравнение семейства окружностей.
Пример2.
Составить дифференциальное уравнение семейства линий  .
.
Решение.  ,
, 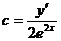

 .
.
Дифференциальные уравнения I-го порядка
С разделяющимися переменными
Определение. Дифференциальное уравнение вида
 (
( ),
),
где  и
и 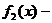 непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
Метод решения такого вида уравнений носит название разделения переменных.
Уравнение ( ) перепишем в виде
) перепишем в виде 
 . Тогда
. Тогда  .
.
Интегрируем  , где
, где  .
.
Пример. 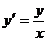 . Найти частное решение при начальных условиях
. Найти частное решение при начальных условиях  .
.
Решение.  .
. 
 или
или 
 .
.
Это общее решение. Частное решение получим, подставляя начальные условия 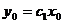 ,
,
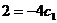 ,
,  . Частное решение исходного уравнении:
. Частное решение исходного уравнении:  .
.
Линейные дифференциальные уравнения
I-го порядка (л.д.у.).
Определение. Уравнение вида
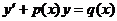 (4),
(4),
где p(x), q(x) - непрерывные функции, называется линейным дифференциальным уравнением первого порядка (л.д.у.).Если q(x)= 0, то уравнение (4) называется однородным принимает вид  . Если q(x)
. Если q(x)  0, то уравнение (4) называется неоднородным.
0, то уравнение (4) называется неоднородным.
Неизвестная функция и её производная входят в указанное уравнение в первой степени линейно, что объясняет название уравнения.
Метод подстановки.
Найти общее решение уравнения 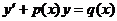 .
.
Положим 
Подставим эти выражения в исходное уравнение:
 .
.
Или 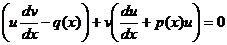 (*)
(*)
Потребуем (или выберем u(x) такое), чтобы  .
.
Найдем u(x) из уравнения  , применив метод разделяющих переменных. Получим
, применив метод разделяющих переменных. Получим  ,
,  .
.
Выберем какое-нибудь частное решение (например, при с =1)  ,
,
подставим в (*), получим  .
.
Найдем общее решение этого уравнения  .
.
Общее решение исходного уравнения имеет вид:  , где
, где
 - частное решение исходного уравнения,
- частное решение исходного уравнения,
 - общее решение исходного уравнения.
- общее решение исходного уравнения.
Замечание. При решении уравнения методом разделенных переменных может быть потеряно решение  , т.е. утеряны интегральные кривые
, т.е. утеряны интегральные кривые  . Поэтому получив методом разделенных переменных общее решение уравнения, нужно проверить, все ли частные решения мы охватили при подходящем значении с. В случае отсутствия, их нужно включить.
. Поэтому получив методом разделенных переменных общее решение уравнения, нужно проверить, все ли частные решения мы охватили при подходящем значении с. В случае отсутствия, их нужно включить.
Пример (потеря решения).
 .
.
Для удобства положим  .
.
Тогда  .
.  .
.
Но исходное уравнение имеет решение у=0, которое не входит в запись  . Поэтому запишем решение как
. Поэтому запишем решение как  , где с может быть равным нулю.
, где с может быть равным нулю.
Итак, получив общее решение, необходимо проверить, входит ли в его состав при подходящих числовых значениях параметра с упомянутые частные решения. Если не входят, то нужно включить.
Пример ( на метод подстановки).  .
.
Положим 

 .
.
Потребуем 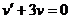 .
.
 .
.
Выберем какое-нибудь частное решение этого уравнения  .
.
Подставим это решение в (*):  ,
,
найдем общее решение методом разделения переменных
 .
.
Отсюда  или
или  .
.
Упражнения.
1. Найти общее решение дифференциальных уравнений 1-го порядка:
1. 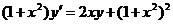 2.
2. 
3.  4.
4. 
5.  6.
6. 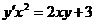
7.  8.
8. 
9.  10.
10. 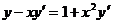
11.  12.
12. 
13. 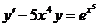 14.
14. 
15. 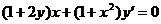
2. Найти общее решение дифференциальных уравнений 2-го порядка:
1. 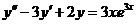 .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10. 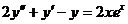 .
.
11.  .
.
12.  .
.
13.  ;
;
14.  .
.
15.  .
.
16. 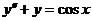 ;
;
17.  ;
;
18. 
19. 
20. 
21.  .
.
Учебное пособие по «Математическому анализу»
Составила Н.И.Макарчук
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения (Д.У.) занимают особое место в математике, имеют многочисленные применения.
Основной задачей теории Д.У. является изучение функций, представляющих собой решение этих уравнений. Если функция зависит от одной переменной, то Д.У. называются обыкновенными. Теория Д.У., когда неизвестные функции зависят от нескольких переменных, является более сложной и представляет специальный раздел математики – уравнения в частных производных.



 . Пусть
. Пусть  его решение, график которого представляет собой непрерывную интегральную кривую, причем в каждой её точке существует касательная. Из записи дифференциального уравнения следует, что угловой коэффициент касательной к интегральной кривой в каждой её точке равен правой части этого уравнения. Следовательно, уравнение I-го порядка задает угловой коэффициент (
его решение, график которого представляет собой непрерывную интегральную кривую, причем в каждой её точке существует касательная. Из записи дифференциального уравнения следует, что угловой коэффициент касательной к интегральной кривой в каждой её точке равен правой части этого уравнения. Следовательно, уравнение I-го порядка задает угловой коэффициент ( )
) сопоставить отрезок направленный под углом наклона
сопоставить отрезок направленный под углом наклона  к оси
к оси 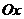 , то мы получим поле направлений данного уравнения. В этом заключается геометрический смысл дифференциального уравнения I-го порядка. Поле направлений позволяет проанализировать решение дифференциального уравнения и даже приближенно построить интегральные кривые.
, то мы получим поле направлений данного уравнения. В этом заключается геометрический смысл дифференциального уравнения I-го порядка. Поле направлений позволяет проанализировать решение дифференциального уравнения и даже приближенно построить интегральные кривые. .
. ,
,

 .
. . Это и есть дифференциальное уравнение семейства окружностей.
. Это и есть дифференциальное уравнение семейства окружностей. .
. ,
, 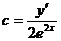

 .
. (
( ),
), и
и 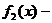 непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
 . Тогда
. Тогда  .
. , где
, где  .
.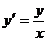 . Найти частное решение при начальных условиях
. Найти частное решение при начальных условиях  .
. .
. 
 или
или 
 .
.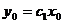 ,
,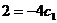 ,
,  . Частное решение исходного уравнении:
. Частное решение исходного уравнении:  .
.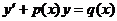 (4),
(4), . Если q(x)
. Если q(x)  0, то уравнение (4) называется неоднородным.
0, то уравнение (4) называется неоднородным.
 .
.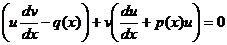 (*)
(*) .
. ,
,  .
. ,
, .
. .
. , где
, где - частное решение исходного уравнения,
- частное решение исходного уравнения, - общее решение исходного уравнения.
- общее решение исходного уравнения. , т.е. утеряны интегральные кривые
, т.е. утеряны интегральные кривые  . Поэтому получив методом разделенных переменных общее решение уравнения, нужно проверить, все ли частные решения мы охватили при подходящем значении с. В случае отсутствия, их нужно включить.
. Поэтому получив методом разделенных переменных общее решение уравнения, нужно проверить, все ли частные решения мы охватили при подходящем значении с. В случае отсутствия, их нужно включить. .
. .
. .
.  .
. . Поэтому запишем решение как
. Поэтому запишем решение как  , где с может быть равным нулю.
, где с может быть равным нулю. .
.

 .
.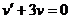 .
. .
. .
. ,
, .
. или
или  .
.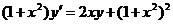 2.
2. 
 4.
4. 
 6.
6. 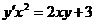
 8.
8. 
 10.
10. 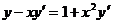
 12.
12. 
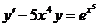 14.
14. 
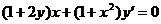
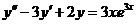 .
. .
. .
. .
. .
. .
. .
. .
. .
.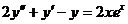 .
. .
. .
. .
. .
.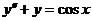 ;
; ;
;


 .
.


