Пусть функция 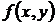 определена в некоторой области G плоскости
определена в некоторой области G плоскости  . Уравнение
. Уравнение
 ,
,  (5)
(5)
задает в каждой точке  , где существует функция
, где существует функция  , значение
, значение  , т.е. угловой коэффициент касательной к интегральной кривой
, т.е. угловой коэффициент касательной к интегральной кривой  в этой точке. Так как с геометрической точке зрения координаты х и у равноправны, наряду с уравнением (5) рассматривать также уравнение
в этой точке. Так как с геометрической точке зрения координаты х и у равноправны, наряду с уравнением (5) рассматривать также уравнение
 ,
,  , (6)
, (6)
которое задает в каждой точке  , где существует функция
, где существует функция  , значение
, значение  , т.е. угловой коэффициент по отношению к оси Оу касательной к интегральной кривой
, т.е. угловой коэффициент по отношению к оси Оу касательной к интегральной кривой  . Очевидно, что имеющий смысл уравнения (5) и (6) эквивалентны, поскольку имеют большие интегральные кривые. Если в некоторых точках области G одно из уравнений не имеет смысла, то используется другое, заменяющее в этих точках первое уравнение. Иногда дифференциальные уравнения первого порядка можно записать в более симметричный относительно х и у форме
. Очевидно, что имеющий смысл уравнения (5) и (6) эквивалентны, поскольку имеют большие интегральные кривые. Если в некоторых точках области G одно из уравнений не имеет смысла, то используется другое, заменяющее в этих точках первое уравнение. Иногда дифференциальные уравнения первого порядка можно записать в более симметричный относительно х и у форме
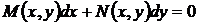 , (7)
, (7)
где функции 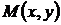 и
и 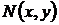 определены в области G.
определены в области G.
Если в каждой точке области G задано значение некоторой величины, то говорят, что в области G задано поле этой величины. Таким образом, дифференциальное уравнение (5) определяет поленаправлений. Тройка чисел  определяет направление отрезка прямой с наклоном
определяет направление отрезка прямой с наклоном  ,проходящей через точку
,проходящей через точку  и называется линейнымэлементом. Совокупность линейных элементов образует поле направлений. Дифференциальное уравнение тем самым отождествляется со своим полем направлений.
и называется линейнымэлементом. Совокупность линейных элементов образует поле направлений. Дифференциальное уравнение тем самым отождествляется со своим полем направлений.
Задача интегрирования в геометрической интерпретации ставится так: в области G найти все линии, имеющие в каждой точке направление, заданное уравнениями (5), (6). Эта математически строгая формулировка для практических целей может быть истолкована конструктивнее: в области G найти некоторые кривые такие, чтобы касательные к ним в каждой точке имели направления, совпадающие с направлениями в этих точках. Эти кривые (линии) называются интегральными кривыми (линиями) рассматриваемого уравнения.
Задача построения интегральной кривой в грубом, нулевом приближении часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и то же направление. Семейство изоклин дифференциального уравнения (5) определяется уравнением
 ,
,  ,
,  , (8)
, (8)
где k – параметр. Придавая параметру k близкие числовые значения, можно получить достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые (геометрический образ общего интеграла) дифференциального уравнения (5) в рассматриваемой области G.
Нулевая изоклина  дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых, она делит область G на части, в каждой из которых
дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых, она делит область G на части, в каждой из которых  сохраняет постоянный знак. Интегральные кривые
сохраняет постоянный знак. Интегральные кривые  , пересекая нулевую изоклину, переходят из области возрастания функции
, пересекая нулевую изоклину, переходят из области возрастания функции  в область убывания или наоборот. Для лучшего качества построения интегральных кривых в сложных случаях находят геометрическое место точек перегиба, в которых
в область убывания или наоборот. Для лучшего качества построения интегральных кривых в сложных случаях находят геометрическое место точек перегиба, в которых 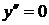 . Дифференцированием по х уравнения (5), с использованием самого уравнения (5), находят
. Дифференцированием по х уравнения (5), с использованием самого уравнения (5), находят

и приравнивают ее к нулю. Линия, определяемая уравнением
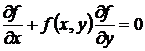 , (9)
, (9)
и есть возможное геометрическое место точек перегиба; она разбивает область G на две части, в одной из которых  , и, следовательно, интегральные кривые выпуклы вверх, а в другой
, и, следовательно, интегральные кривые выпуклы вверх, а в другой  , и значит, интегральные кривые вогнуты вверх.
, и значит, интегральные кривые вогнуты вверх.
Примеры.

7.

. В данном случае изоклинами являются (рис. 1) полупрямые

, в которых угловой коэффициент касательной к искомой интегральной кривой. Интегральными кривыми будут полупрямые
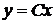
. Здесь начало координат (0,0) – особая точка уравнения, в ней не определено поле направления, поскольку правая часть уравнения обращается в неопределенность

.
 8.
8.  . Уравнение изоклин получим, полагая (рис. 2)
. Уравнение изоклин получим, полагая (рис. 2) 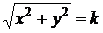 или
или  , следовательно, в данном случае изоклинами являются окружности с центром в начале координат; угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Задавая масштаб, дадим постоянной k некоторые определенные значения, например,
, следовательно, в данном случае изоклинами являются окружности с центром в начале координат; угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Задавая масштаб, дадим постоянной k некоторые определенные значения, например,  ,
,  , 1,
, 1, 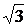 , 3. Тогда, согласно формуле
, 3. Тогда, согласно формуле
(8), углы наклона линейных элементов на этих окружностях будут выражены (в градусах) соответственно  , 30, 45, 60,
, 30, 45, 60,  . Общее решение данного уравнения в окрестности начала координат схематично показано на рис. 2.
. Общее решение данного уравнения в окрестности начала координат схематично показано на рис. 2.
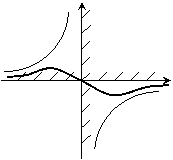
9.

. Изоклинами этого уравнения являются гиперболы

или

, при параметре
k принимающем положительные и отрицательные значения. При
k =0 получаем нулевую изоклину;
k =1 гипербола распадается на пару прямых
х =0 и
у =0. При переходе через нулевую изоклину величина

меняет свой знак, как показано на рис. 3. Применяя формулу (9), находим линию точки перегиба интегральных кривых
 или
или  ,
,
отсюда  .
.
При переходе через эту линию интегральные кривые переходят от выпуклости  к вогнутости
к вогнутости  , как показано на рис. 3, где линия точек перегиба выделена жирно. Рассматривая разность между этой линией и нулевой изоклиной
, как показано на рис. 3, где линия точек перегиба выделена жирно. Рассматривая разность между этой линией и нулевой изоклиной
 ,
, 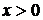 ,
,
видим, что она положительна в правой полуплоскости и отрицательна в левой. Следовательно, линия точек перегиба проходит под нулевой изоклиной, при  , и над нулевой изоклиной, если
, и над нулевой изоклиной, если 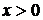 , и эти линии никогда не пересекаются. Однако, решая совместное уравнение
, и эти линии никогда не пересекаются. Однако, решая совместное уравнение

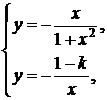

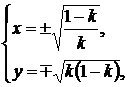
убеждаемся, что при  существует их решение, совпадающее с координатами точки касания гиперболы
существует их решение, совпадающее с координатами точки касания гиперболы 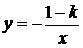 и прямой с угловым коэффициентом равным k. Этих сведений достаточно, чтобы сделать набросок расположения интегральных кривых (рис. 4).
и прямой с угловым коэффициентом равным k. Этих сведений достаточно, чтобы сделать набросок расположения интегральных кривых (рис. 4).
Трудами многих ученых в течение XVIII века был накоплен большой опыт по составлению дифференциальных уравнений и нахождению их общих решений или общих интегралов в различных приложениях. Обычный подход заключался в предварительном разыскании общих интегралов, содержащих неизвестные функции и константы, и лишь затем в подборе констант и определении неизвестных функций. О. Коши (1789–1857) в своих работах отмечал, что на практике наибольший интерес представляют частные решения, в которых произвольные постоянные определены исходя из некоторых стандартных условий, названных им начальными условиями. Начальными они названы потому, что изначально фиксируется значение  независимой переменной х и выбираются (считающимися известными из практических или иных соображений) значения
независимой переменной х и выбираются (считающимися известными из практических или иных соображений) значения  неизвестной функции и ее производных до
неизвестной функции и ее производных до  -го порядка, если рассматривается уравнение (1). Для дифференциального уравнения первого порядка начальная задача ставится так.
-го порядка, если рассматривается уравнение (1). Для дифференциального уравнения первого порядка начальная задача ставится так.
Задача Коши. Пусть функция 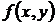 определена и непрерывна по переменным х, у и имеет ограниченную частную производную
определена и непрерывна по переменным х, у и имеет ограниченную частную производную  по переменной у в замкнутой области
по переменной у в замкнутой области  , например (рис. 5),
, например (рис. 5),  .
.
Найти функцию 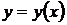 , удовлетворяющую уравнению
, удовлетворяющую уравнению
 (5)
(5)
и условию  ,
,  . (10)
. (10)
поставленная задача Коши всегда имеет единственное решение, которое может быть найдено, например, методом последовательных приближений Пикара (1856–1941). Заслуга Коши заключается в том, что он доказал существование и единственность начальной задачи не только для уравнения (5), но и для упоминавшейся выше нормальной системы и тем самым резко упростил нахождение нужных на практике решений.
 С геометрической точки зрения решить задачу Коши значит найти интегральную кривую
С геометрической точки зрения решить задачу Коши значит найти интегральную кривую 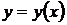 , проходящую через заданную внутри области G точку
, проходящую через заданную внутри области G точку  .
.
Условия (10) называются начальными условиями решения 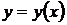 , а числа
, а числа  и
и 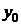 – начальными данными этого решения. Задача нахождения решения уравнения (5), удовлетворяющего заданным начальным условиям (10) называется задачей Коши. Вообще решение задачи Коши для уравнения (5) в любой из форм (6),
– начальными данными этого решения. Задача нахождения решения уравнения (5), удовлетворяющего заданным начальным условиям (10) называется задачей Коши. Вообще решение задачи Коши для уравнения (5) в любой из форм (6),
(7) его записи ищут в том виде, в каком это оказывается наиболее удобно, т.е. в виде 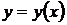 ,
,  ,
,  или в параметрической форме
или в параметрической форме  ,
,  .
.
Решение задачи коши стараются найти в элементарных функциях или в квадратурах от элементарных функций. В тех случаях, когда это не удается, приходится прибегать к приближенным методам интегрирования, в основе которых лежит метод ломаных Эйлера, предложенный знаменитым математиком членом Петербургской академии наук, Леонардом Эйлером (1707–1783). Более того, метод Эйлера лежит в основе теорем о существовании и единственности поставленной задачи (5), (10) Коши, поэтому рассмотрим его подробнее.
Как известно, уравнение (5) с заданной в области G функции 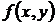 определяет в G после направлений, которые должны иметь интегральные линии.
определяет в G после направлений, которые должны иметь интегральные линии.
Возьмем в области G точку  . Ей будет соответствовать проходящая через эту точку прямая с угловым коэффициентом
. Ей будет соответствовать проходящая через эту точку прямая с угловым коэффициентом  . На этой прямой в области G возьмем точку
. На этой прямой в области G возьмем точку  (на рис. 5 обозначена цифрой 1). Через точку
(на рис. 5 обозначена цифрой 1). Через точку  проведем прямую с угловым коэффициентом
проведем прямую с угловым коэффициентом  , на которой отметим принадлежащую G точку
, на которой отметим принадлежащую G точку  (на рис. 5 обозначена цифрой 2). Затем на прямой, соответствующей точке
(на рис. 5 обозначена цифрой 2). Затем на прямой, соответствующей точке  , отмечаем точку
, отмечаем точку  и т.д. Пусть при этом
и т.д. Пусть при этом  такое построение можно выполнять и в сторону убывающих значений х. Получим ломаные линии, которые называют ломаными Эйлера. Естественно ожидать, что каждая из ломаных Эйлера с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку
такое построение можно выполнять и в сторону убывающих значений х. Получим ломаные линии, которые называют ломаными Эйлера. Естественно ожидать, что каждая из ломаных Эйлера с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку  , и что при уменьшении длин звеньев ломаные Эйлера будут приближаться к этой интегральной кривой. Для численных расчетов интервал непрерывного изменения аргумента
, и что при уменьшении длин звеньев ломаные Эйлера будут приближаться к этой интегральной кривой. Для численных расчетов интервал непрерывного изменения аргумента  заменяем дискретным множеством точек
заменяем дискретным множеством точек  ,
,  , где h – малое число, называемое параметром или шагом сетки
, где h – малое число, называемое параметром или шагом сетки  . Если
. Если  , то сетка называется равномерной. Заменяя производную в уравнении (5) отношением конечных приращений
, то сетка называется равномерной. Заменяя производную в уравнении (5) отношением конечных приращений

 ,
,
с учетом правой части уравнения (5) и условий (10) имеем законченный вычислительный алгоритм интегрирования
 ,
,  ,
,  .
.
Погрешность этого метода на всем интервале при малом параметре h порядка h, поэтому целесообразно для повышения точности уменьшать шаг.



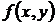 определена в некоторой области G плоскости
определена в некоторой области G плоскости  . Уравнение
. Уравнение ,
,  (5)
(5) , значение
, значение  , т.е. угловой коэффициент касательной к интегральной кривой
, т.е. угловой коэффициент касательной к интегральной кривой  в этой точке. Так как с геометрической точке зрения координаты х и у равноправны, наряду с уравнением (5) рассматривать также уравнение
в этой точке. Так как с геометрической точке зрения координаты х и у равноправны, наряду с уравнением (5) рассматривать также уравнение ,
,  , (6)
, (6) , значение
, значение  , т.е. угловой коэффициент по отношению к оси Оу касательной к интегральной кривой
, т.е. угловой коэффициент по отношению к оси Оу касательной к интегральной кривой  . Очевидно, что имеющий смысл уравнения (5) и (6) эквивалентны, поскольку имеют большие интегральные кривые. Если в некоторых точках области G одно из уравнений не имеет смысла, то используется другое, заменяющее в этих точках первое уравнение. Иногда дифференциальные уравнения первого порядка можно записать в более симметричный относительно х и у форме
. Очевидно, что имеющий смысл уравнения (5) и (6) эквивалентны, поскольку имеют большие интегральные кривые. Если в некоторых точках области G одно из уравнений не имеет смысла, то используется другое, заменяющее в этих точках первое уравнение. Иногда дифференциальные уравнения первого порядка можно записать в более симметричный относительно х и у форме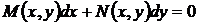 , (7)
, (7)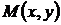 и
и 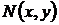 определены в области G.
определены в области G. определяет направление отрезка прямой с наклоном
определяет направление отрезка прямой с наклоном  ,проходящей через точку
,проходящей через точку  ,
,  ,
,  , (8)
, (8) дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых, она делит область G на части, в каждой из которых
дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых, она делит область G на части, в каждой из которых  в область убывания или наоборот. Для лучшего качества построения интегральных кривых в сложных случаях находят геометрическое место точек перегиба, в которых
в область убывания или наоборот. Для лучшего качества построения интегральных кривых в сложных случаях находят геометрическое место точек перегиба, в которых 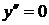 . Дифференцированием по х уравнения (5), с использованием самого уравнения (5), находят
. Дифференцированием по х уравнения (5), с использованием самого уравнения (5), находят
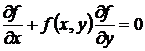 , (9)
, (9) , и, следовательно, интегральные кривые выпуклы вверх, а в другой
, и, следовательно, интегральные кривые выпуклы вверх, а в другой  , и значит, интегральные кривые вогнуты вверх.
, и значит, интегральные кривые вогнуты вверх. 7.
7.  . В данном случае изоклинами являются (рис. 1) полупрямые
. В данном случае изоклинами являются (рис. 1) полупрямые  , в которых угловой коэффициент касательной к искомой интегральной кривой. Интегральными кривыми будут полупрямые
, в которых угловой коэффициент касательной к искомой интегральной кривой. Интегральными кривыми будут полупрямые 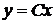 . Здесь начало координат (0,0) – особая точка уравнения, в ней не определено поле направления, поскольку правая часть уравнения обращается в неопределенность
. Здесь начало координат (0,0) – особая точка уравнения, в ней не определено поле направления, поскольку правая часть уравнения обращается в неопределенность  .
.
 8.
8.  . Уравнение изоклин получим, полагая (рис. 2)
. Уравнение изоклин получим, полагая (рис. 2) 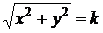 или
или  , следовательно, в данном случае изоклинами являются окружности с центром в начале координат; угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Задавая масштаб, дадим постоянной k некоторые определенные значения, например,
, следовательно, в данном случае изоклинами являются окружности с центром в начале координат; угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Задавая масштаб, дадим постоянной k некоторые определенные значения, например,  ,
,  , 1,
, 1, 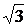 , 3. Тогда, согласно формуле
, 3. Тогда, согласно формуле , 30, 45, 60,
, 30, 45, 60,  . Общее решение данного уравнения в окрестности начала координат схематично показано на рис. 2.
. Общее решение данного уравнения в окрестности начала координат схематично показано на рис. 2.




 . Изоклинами этого уравнения являются гиперболы
. Изоклинами этого уравнения являются гиперболы  или
или  , при параметре k принимающем положительные и отрицательные значения. При k =0 получаем нулевую изоклину; k =1 гипербола распадается на пару прямых х =0 и у =0. При переходе через нулевую изоклину величина
, при параметре k принимающем положительные и отрицательные значения. При k =0 получаем нулевую изоклину; k =1 гипербола распадается на пару прямых х =0 и у =0. При переходе через нулевую изоклину величина  или
или  ,
, .
. к вогнутости
к вогнутости  , как показано на рис. 3, где линия точек перегиба выделена жирно. Рассматривая разность между этой линией и нулевой изоклиной
, как показано на рис. 3, где линия точек перегиба выделена жирно. Рассматривая разность между этой линией и нулевой изоклиной ,
, 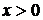 ,
, , и над нулевой изоклиной, если
, и над нулевой изоклиной, если 
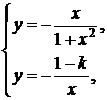

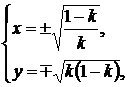
 существует их решение, совпадающее с координатами точки касания гиперболы
существует их решение, совпадающее с координатами точки касания гиперболы 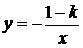 и прямой с угловым коэффициентом равным k. Этих сведений достаточно, чтобы сделать набросок расположения интегральных кривых (рис. 4).
и прямой с угловым коэффициентом равным k. Этих сведений достаточно, чтобы сделать набросок расположения интегральных кривых (рис. 4). независимой переменной х и выбираются (считающимися известными из практических или иных соображений) значения
независимой переменной х и выбираются (считающимися известными из практических или иных соображений) значения  неизвестной функции и ее производных до
неизвестной функции и ее производных до  -го порядка, если рассматривается уравнение (1). Для дифференциального уравнения первого порядка начальная задача ставится так.
-го порядка, если рассматривается уравнение (1). Для дифференциального уравнения первого порядка начальная задача ставится так. по переменной у в замкнутой области
по переменной у в замкнутой области  , например (рис. 5),
, например (рис. 5),  .
.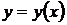 , удовлетворяющую уравнению
, удовлетворяющую уравнению ,
,  . (10)
. (10) С геометрической точки зрения решить задачу Коши значит найти интегральную кривую
С геометрической точки зрения решить задачу Коши значит найти интегральную кривую  .
. и
и 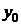 – начальными данными этого решения. Задача нахождения решения уравнения (5), удовлетворяющего заданным начальным условиям (10) называется задачей Коши. Вообще решение задачи Коши для уравнения (5) в любой из форм (6),
– начальными данными этого решения. Задача нахождения решения уравнения (5), удовлетворяющего заданным начальным условиям (10) называется задачей Коши. Вообще решение задачи Коши для уравнения (5) в любой из форм (6), ,
,  или в параметрической форме
или в параметрической форме  ,
,  .
. . Ей будет соответствовать проходящая через эту точку прямая с угловым коэффициентом
. Ей будет соответствовать проходящая через эту точку прямая с угловым коэффициентом  . На этой прямой в области G возьмем точку
. На этой прямой в области G возьмем точку  (на рис. 5 обозначена цифрой 1). Через точку
(на рис. 5 обозначена цифрой 1). Через точку  , на которой отметим принадлежащую G точку
, на которой отметим принадлежащую G точку  (на рис. 5 обозначена цифрой 2). Затем на прямой, соответствующей точке
(на рис. 5 обозначена цифрой 2). Затем на прямой, соответствующей точке  и т.д. Пусть при этом
и т.д. Пусть при этом  такое построение можно выполнять и в сторону убывающих значений х. Получим ломаные линии, которые называют ломаными Эйлера. Естественно ожидать, что каждая из ломаных Эйлера с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку
такое построение можно выполнять и в сторону убывающих значений х. Получим ломаные линии, которые называют ломаными Эйлера. Естественно ожидать, что каждая из ломаных Эйлера с достаточно короткими звеньями дает некоторое представление об интегральной кривой, проходящей через точку  заменяем дискретным множеством точек
заменяем дискретным множеством точек  ,
,  , где h – малое число, называемое параметром или шагом сетки
, где h – малое число, называемое параметром или шагом сетки  . Если
. Если  , то сетка называется равномерной. Заменяя производную в уравнении (5) отношением конечных приращений
, то сетка называется равномерной. Заменяя производную в уравнении (5) отношением конечных приращений
 ,
, ,
,  ,
,  .
.

