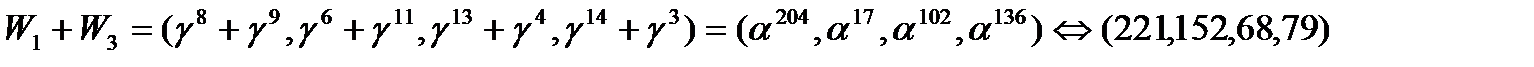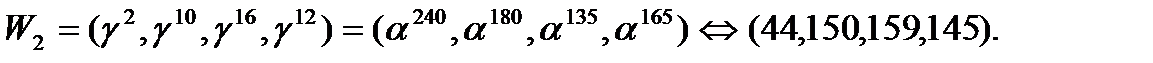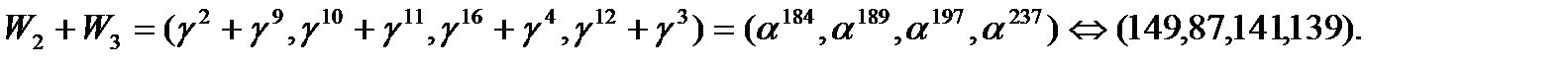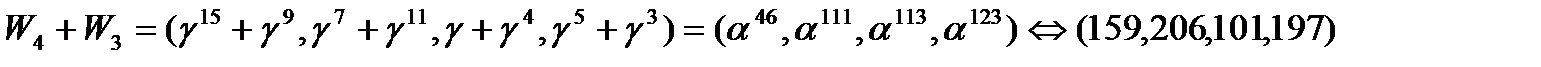Пусть 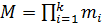 –произведение целых положительных попарно взаимно-простых положительных чисел, пусть
–произведение целых положительных попарно взаимно-простых положительных чисел, пусть 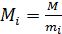 и пусть
и пусть 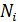 удовлетворяют равенству
удовлетворяют равенству 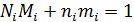 , тогда единственным решением системы сравнений
, тогда единственным решением системы сравнений
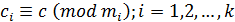
будет
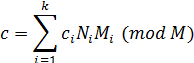
Эта теорема позволяет каждое число n,0≤n<Mоднозначно задать системой остатков по модулям  , i=1,k.
, i=1,k.
4.3. Трехмерное преобразование Фурье в поле 
Рассмотрим ДПФ длины N=255, ядром которого является примитивный элемент поля  .
.
В этом случае, М=255=3

5

17,
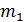
=3,
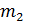
= 5,
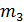
=17, так что n
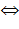
(
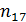
,
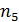
,
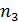
), где
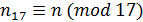 ,
,  ,
, 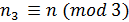
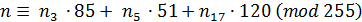
Произвольный ненулевой элемент 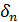 поля
поля 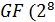 ) задается как степень примитивного элемента
) задается как степень примитивного элемента 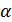 поля:
поля: 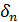 =
= 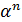 ,
, 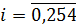
Согласно (2)
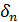
=
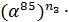
(
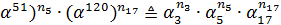
,
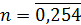 ,
, 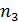 =
=  ,
, 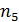 =
= 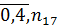 =
=  ,
,
Где приняты обозначения: 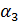 =
= 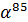 ,
, 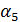 =
=  ,
, 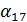 =
= 
Более того, в силу попарной взаимной простоты модулей 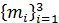 , если i
, если i 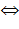 (
(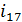 ,
, 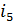 ,
, 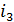 ) и j
) и j 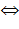 (
(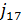 ,
, 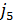 ,
,  ), то ij
), то ij 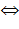 (
(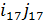 ,
, 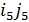 ,
, 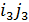 ). Таким образом, формулу (4.1) определяющую ДПФ, можно переписать в виде:
). Таким образом, формулу (4.1) определяющую ДПФ, можно переписать в виде:
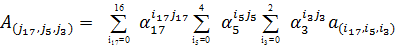
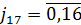 ,
, 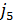 =
=  ,
,  =
= 
Это сразу подсказывает следующий алгоритм вычисления вектора  по вектору
по вектору 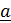 . Сначала разбиваем координаты вектора
. Сначала разбиваем координаты вектора 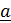 на тройки чисел (прификсированных
на тройки чисел (прификсированных 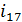 и
и 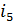 ) и к каждой из них применяем 3-точечное преобразование с ядром
) и к каждой из них применяем 3-точечное преобразование с ядром 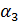 =
= 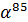 ; это дает набор из 255 величин
; это дает набор из 255 величин
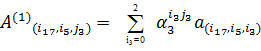
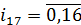 ,
, 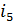 =
=  ,
,  =
=  .
.
Затем к этому вектору 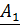 длины 255 применяется 5-точечное ДПФ с ядром
длины 255 применяется 5-точечное ДПФ с ядром 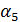 =
=  по правилу: координаты вектора
по правилу: координаты вектора 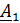 группируются по 5 чисел (по фиксированным
группируются по 5 чисел (по фиксированным 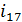 и
и  ) и для каждой такой совокупности вычисляется 5-мерный вектор
) и для каждой такой совокупности вычисляется 5-мерный вектор 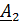 ,
,
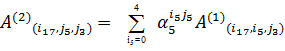
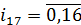 ,
, 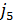 =
=  ,
,  =
=  .
.
Наконец, к вектору 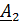 длины 255 применяется 17-точечное ДПФ с ядром
длины 255 применяется 17-точечное ДПФ с ядром 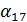 =
=  , приводящее к искомому 255-мерному вектору
, приводящее к искомому 255-мерному вектору  :
:
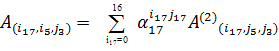
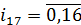 ,
, 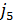 =
=  ,
,  =
=  .
.
Описанный алгоритм вместо
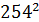
умножений при прямом вычислении по формуле (4.1) требует
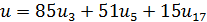
умножений, где
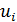
- число умножений, необходимое для выполнения i-точечного ДПФ, i=3,5,17. Аналогично выписывается и формула для числа сложений (кстати, напомним, что характеристика рассматриваемого поля равна 2, так что вычитание совпадает со сложением)

Экспериментально установлено, что переход от одномерной структуры к трехмерной, уменьшает время, требуемое на вычисление ДПФ примерно в 10 раз.
Таким образом, переход от ДПФ длины 255 к ДПФ длин 3, 5 и 17, каждое из которых вычисляется 255 раз в цикле, очень существенно понижает вычислительную сложность алгоритма.
Следующий наш шаг – полностью избавиться от ДПФ внутри циклов, заменив их на БПФ (быстрое преобразование Фурье) длин 3, 5 и 17, которые основаны как на свойствах поля  , так и на свойствах алгоритмов быстрого умножения многочленов, заданных над конечным полем.
, так и на свойствах алгоритмов быстрого умножения многочленов, заданных над конечным полем.
4.4 Быстрое преобразование Фурье БПФ длины 3
3-точечное ДПФ с ядромβдля вектора  задается формулой
задается формулой
 )=
)= 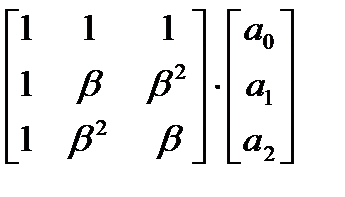
Так как ядро β удовлетворяет тождеству 1+  , то легко проверить непосредственно, что числа
, то легко проверить непосредственно, что числа  могут быть вычислены по правилу:
могут быть вычислены по правилу:
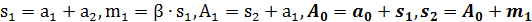
 , которое содержит только одно умножение и 5 сложений (вместо 4 умножений и 6 сложений). Если
, которое содержит только одно умножение и 5 сложений (вместо 4 умножений и 6 сложений). Если  ,
,  .
.
4.5. Быстрое преобразование Фурье длины 5
5-точечное ДПФ с ядром 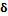 задается равенством
задается равенством
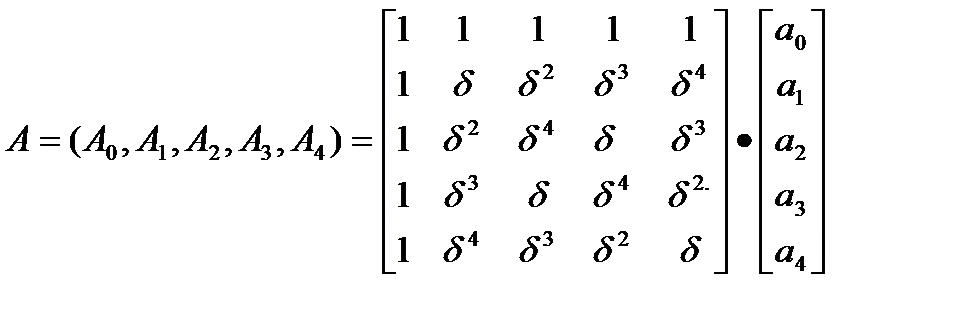 ,
,
непосредственное вычисление по которому требует 16 умножений и 20 сложений. Использование только тождества на ядре (которое в данном случае имеет вид 1+ 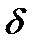 +
+ 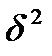 +
+ 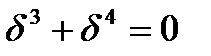 ) дает 9 умножений и 21 сложение. Это достигается, например, следующим образом:
) дает 9 умножений и 21 сложение. Это достигается, например, следующим образом:
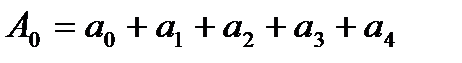 ,
,
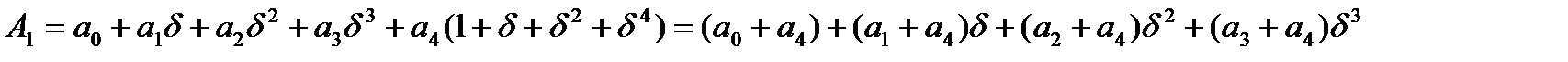 Аналогично,
Аналогично,
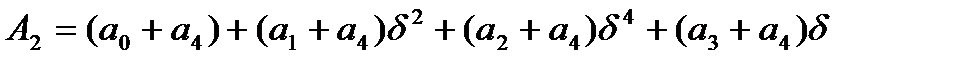 ,
,
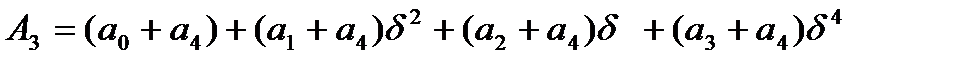 ,
,
и, наконец,
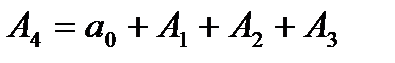
Дальнейшего уменьшения числа умножений можно добиться за счет перехода к циркулянту и использования полиномиальной свертки (ПС). Приведем необходимые сведения:
Утверждение 4.5.1. Два двучлена 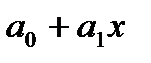 и
и 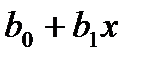 ,
, 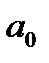 ,
, 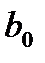 ,
, 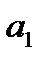 ,
,  , можно перемножить, выполняя не более трех умножений чисел в поле F.
, можно перемножить, выполняя не более трех умножений чисел в поле F.
Действительно, (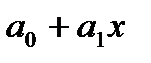 )(
)(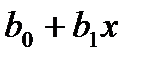 )≜
)≜ 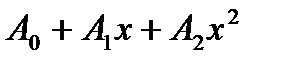 , где
, где  ,
, 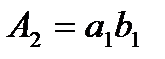 и
и 
Если умножение происходит вполе F 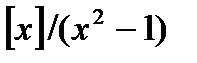 , то
, то  , где
, где 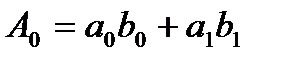 ,
, 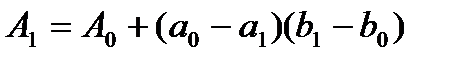
Следствие 4.5.1. Два многочлена степени m над полем F можно перемножить, выполняя не более 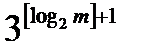 умножений чисел в поле F.
умножений чисел в поле F.
Например, для m=3 (с учетом, что charGF(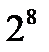 )=2) имеем:
)=2) имеем:
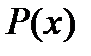
≜
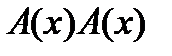
≜

=
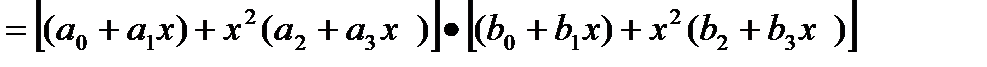 ≜
≜ 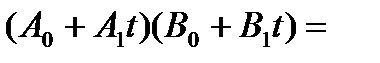
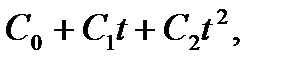
где t≜  (так что при вычислении по модулю многочлена
(так что при вычислении по модулю многочлена 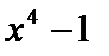 надо делать редукцию по модулю
надо делать редукцию по модулю  ); согласно утверждению 4.5.1:
); согласно утверждению 4.5.1:
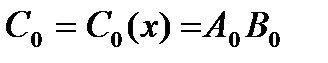 ≜
≜ 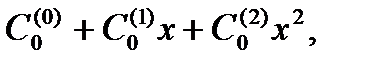
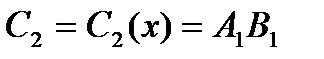 ≜
≜ 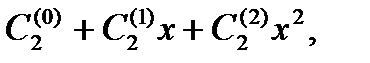
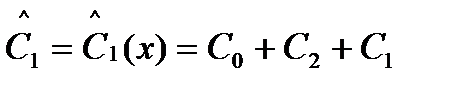
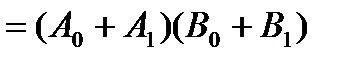 ≜
≜ 
Для вычисления  ,
, 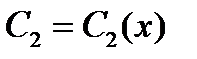 ,
, 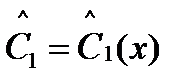 опять воспользуемся утверждением 4.5.1. Имеем
опять воспользуемся утверждением 4.5.1. Имеем
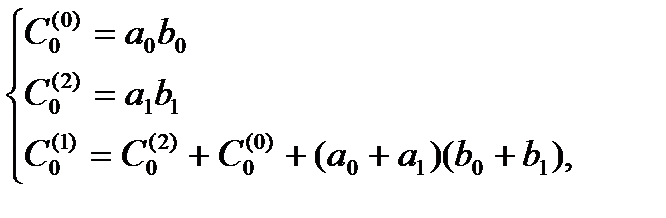
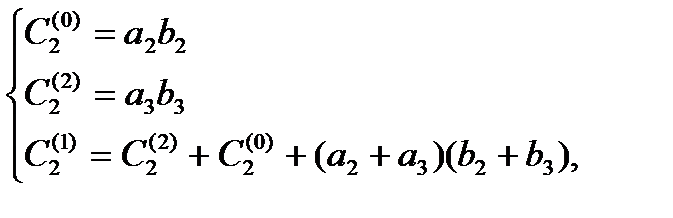
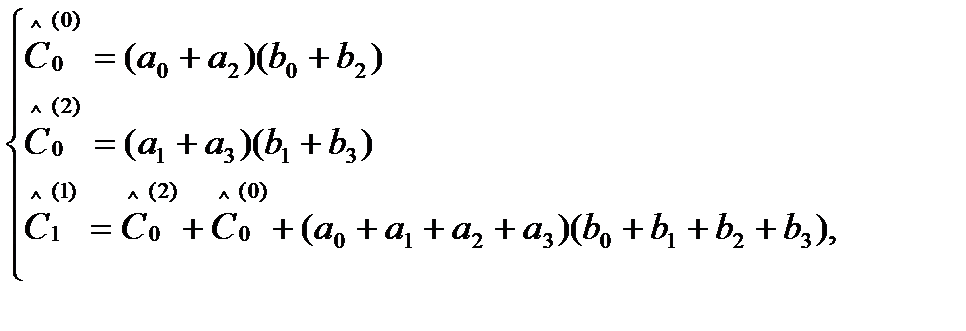
Таким образом, для вычисления коэффициентов 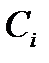 многочлена
многочлена  необходимо только 9 (вместо 16) умножений. Точные формулы для коэффициентов многочлена
необходимо только 9 (вместо 16) умножений. Точные формулы для коэффициентов многочлена 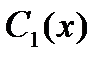 (при
(при 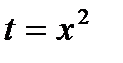 ) имеют вид:
) имеют вид:

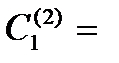
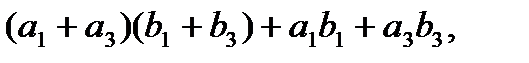
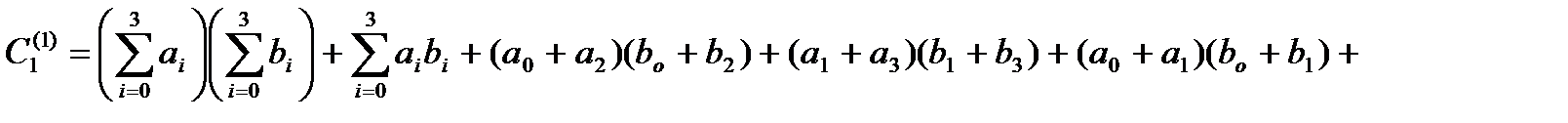
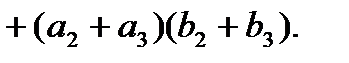
Для коэффициентов 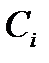 при
при 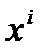 , согласно (10)-(12)
, согласно (10)-(12)
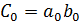 ,
,
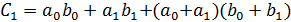 ,
,
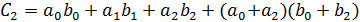 ,
,
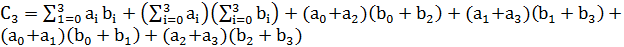 ,
,
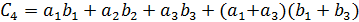
,
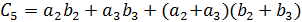 ,
,
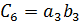 ,
,
Если произведение  вычисляется в кольце F
вычисляется в кольце F 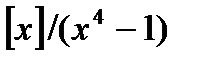 (так что
(так что 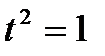 ), то формулы (10)-(12) принимают вид:
), то формулы (10)-(12) принимают вид:
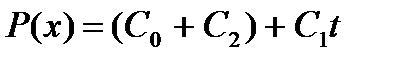 ≜
≜ 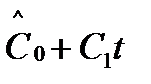 , (10а)
, (10а)

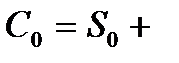
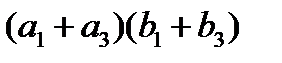 ,
,  ≜
≜ 
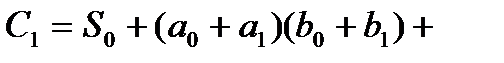
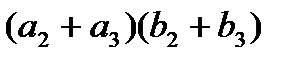 ,
,
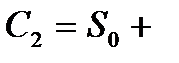
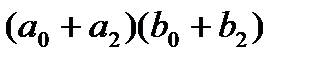
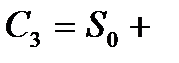
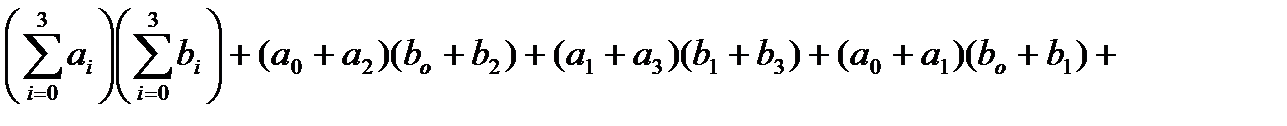
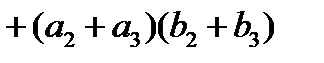 .
.
Вычисление вектора 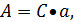 где
где 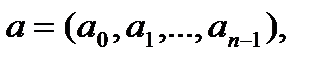 а
а 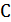 – циркулянт, первая строка которого задается вектором
– циркулянт, первая строка которого задается вектором 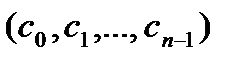 , равносильно вычислению в F
, равносильно вычислению в F 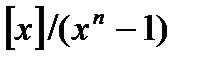 произведения
произведения 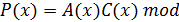
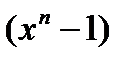 , где
, где 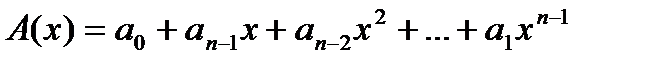 и
и 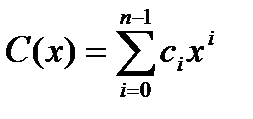 .
.
Подчеркнем, что преобразуемая последовательность 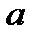 , за исключением первого элемента, дает реверсивный порядок коэффициентов многочлена
, за исключением первого элемента, дает реверсивный порядок коэффициентов многочлена 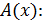 при
при 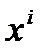 координате стоит коэффициент
координате стоит коэффициент 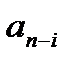 .
.
Утверждение 4.5.2. Для ДПФ простой длины n всегда существует такая перестановка строк и столбцов матрицы Фурье, что она может быть превращена в окаймленный циркулянт.
Этот результат принадлежит Рейдеру. Мы подробно проиллюстрируем соответствующий алгоритм в следующем пункте, посвященному БПФ длины 17, а сейчас вернемся к БПФ длины 5.
Прежде всегоизбавимся от единичного окаймления матрицы Фурье:
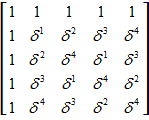

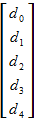 =
= 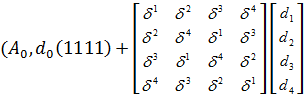 )
)
В столбцах и строках матрицы, стоящей в правой части равенства выполним перестановку  .Если выполним такую же перестановку координат у векторов d и его спектра А, получаем
.Если выполним такую же перестановку координат у векторов d и его спектра А, получаем
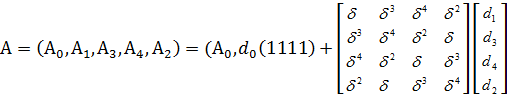 )
) 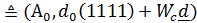 (14)
(14)
Циркулярная матрица 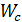 для БПФ длины 5 получается, если задать нумерацию ненулевого элемента поля GF (5) с образующей 3:
для БПФ длины 5 получается, если задать нумерацию ненулевого элемента поля GF (5) с образующей 3: 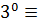 1 (mod5), 3
1 (mod5), 3 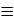 3 (mod5),
3 (mod5), 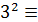 4 (mod5),
4 (mod5), 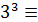 2 (mod5):
2 (mod5): 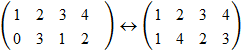 .
.
Этим задача свелась, согласно утверждения 4.5.2, к вычислению многочлена c (x)=d(x)w(x)mod(x  -1), где d(x)=
-1), где d(x)= 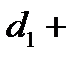
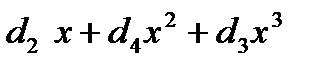 или, иначе, циклической свертки с=с
или, иначе, циклической свертки с=с 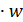
Для вычисления этой циклической свертки длины 4, перепишем формулы (13) в более удобном для организации экономного вычисления виде:
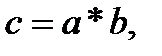
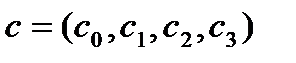 ,
, 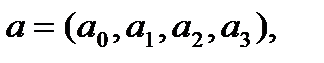
 ;
;
 (15)
(15)
Этот алгоритм содержит 9 умножений и 17 сложений. Но если появляются какие-то условия на коэффициенты 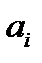 или
или 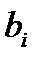 ,то число вычислений уменьшается. Например, если
,то число вычислений уменьшается. Например, если 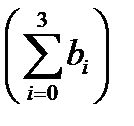 =0 или 1, то число умножений равно только 5. В нашем случае
=0 или 1, то число умножений равно только 5. В нашем случае 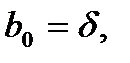
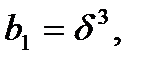
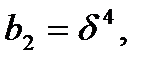
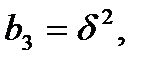 и так как
и так как 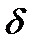 - ядро БПФ длины 5, то
- ядро БПФ длины 5, то 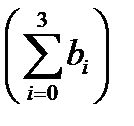 =1. Учитывая это, из формул (13) – (14) окончательно приходим к следующему алгоритму:
=1. Учитывая это, из формул (13) – (14) окончательно приходим к следующему алгоритму:
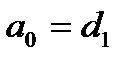 ,
, 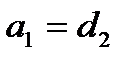 ,
, 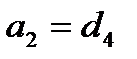 ,
, 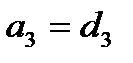 ,
, 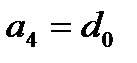 ,
, 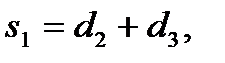
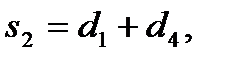
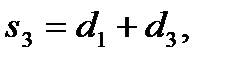
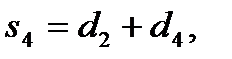
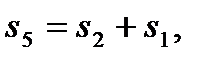
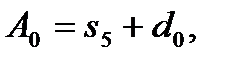
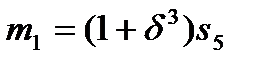 ,
, 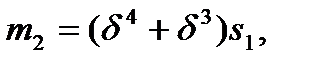
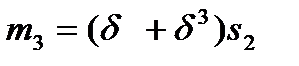 ,
, 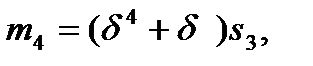
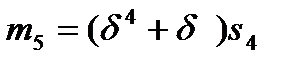 ,
, 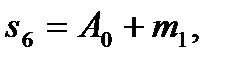
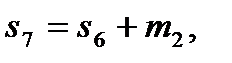
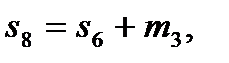

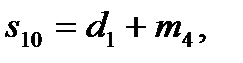
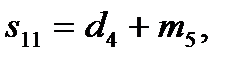

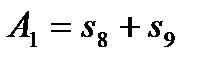 ,
,  ,
, 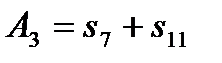 ,
, 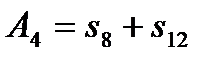 . (16)
. (16)
Так что алгоритм БПФ длины 5 в поле 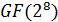 в нашем случае содержит 5 умножений и 11сложений.
в нашем случае содержит 5 умножений и 11сложений.
4.6 Быстрое преобразование Фурье длины 17
17-точечное ДПФ с ядром 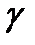 задается равенством
задается равенством
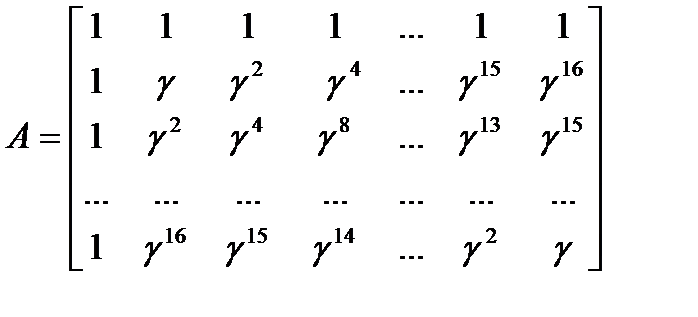
 (17)
(17)
В 
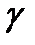 =
= 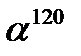 .
.
Для уменьшения числа умножений, как и для 5-точечного ДПФ, воспользуемся переходом к циклической свертке с последующей редукцией по следствию из утверждения 4.5.1. Сначала воспользуемся алгоритмом Рейдерадля перехода к циркулянту. Так как 5 является примитивным элементом поля GF(17), то имеем:
| i
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
|
N=5 
| 5 8 6 13 14 2 10 16 12 9 11 4 3 15 7 1
|
Таким образом, без учета в нумерации одиночного окаймления, к циклической свертке приводит, например, такая перестановка строки столбцов матрицы Фурье в (17) (соответствующих координат преобразуемого вектора а и спектра А), которая дается второй строкой этой таблицы: единичное окаймление остается на месте, а первая строка циркулянта  соответственно имеет вид:
соответственно имеет вид: 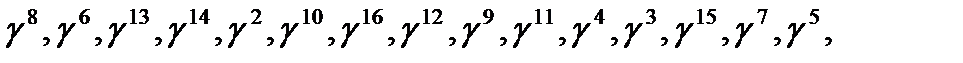
получаем,

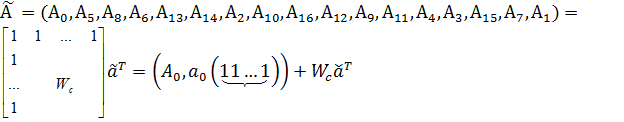
, (18)
где 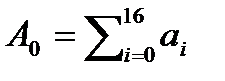 ,
, 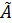 – вектор, полученный из спектра А указанной перестановкой координат, а
– вектор, полученный из спектра А указанной перестановкой координат, а 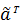 - вектор столбец, определяемый вторым равенством в (18).
- вектор столбец, определяемый вторым равенством в (18).
Согласно утверждению 4.5.2, задача вычисления (18) эквивалентна задаче вычисления циклической свертки
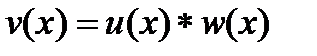
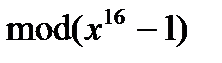 (19)
(19)
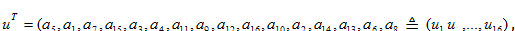
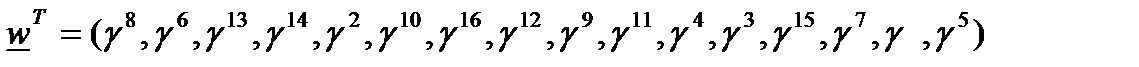
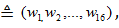
Вычислять свертку (19) будем следующим образом. Пусть 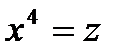 (так что
(так что 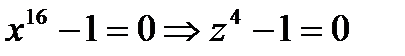 ) и пусть
) и пусть
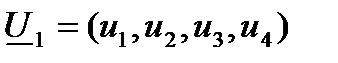
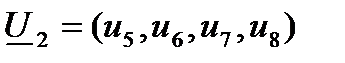
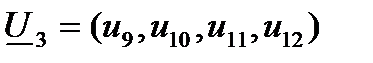
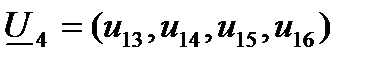
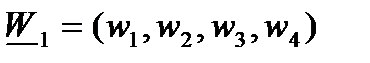
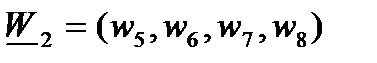
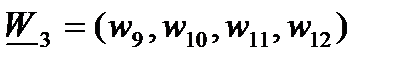

Так что
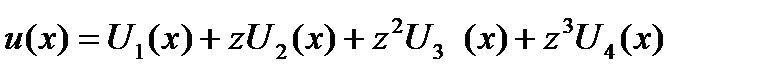
 ,
,
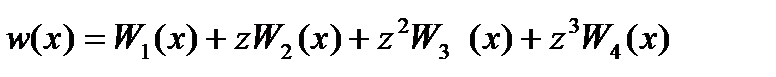
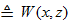 ,
,

Сначала будем полагать переменную х параметром и найдем циклическую свертку по модулю 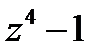 . Обозначая
. Обозначая 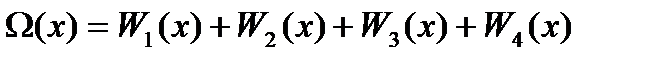 , согласно равенствам (15) имеем:
, согласно равенствам (15) имеем:
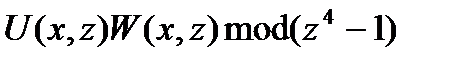
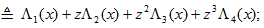
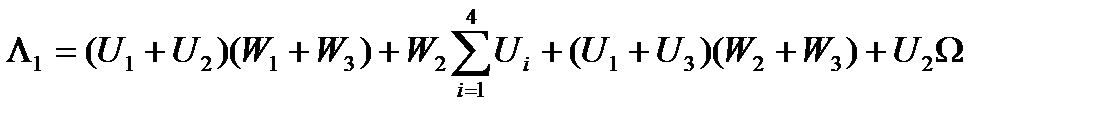
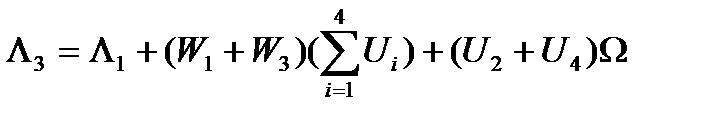 (20)
(20)
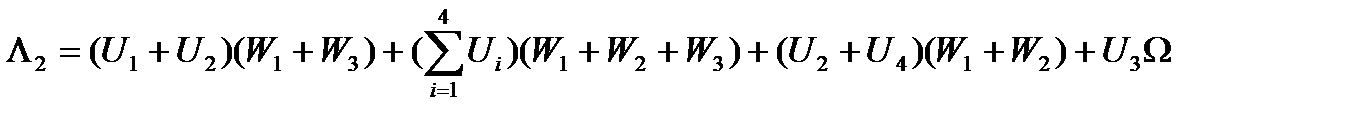
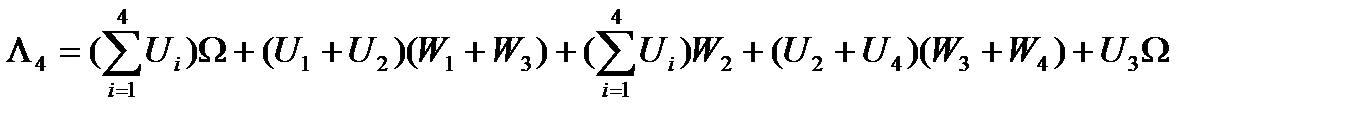
В поле 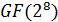 для элемента
для элемента 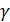 выполняется тождества:
выполняется тождества:
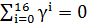 ;
;  ;
; 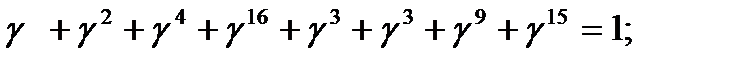
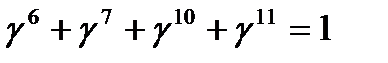 (21)
(21)
Эти тождества позволяют упростить вычисления величин, входящих в (20). Например,
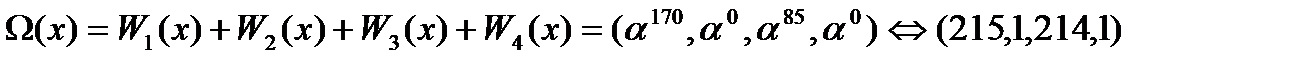
Aлгоритм вычисления R(x)=r(x) 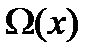 для произвольного многочлена
для произвольного многочлена 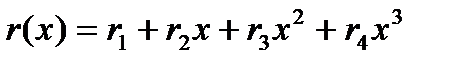 содержит 4 умножения и 12 сложений. А именно, воспользуемся равенством (12) и учтем, что в поле
содержит 4 умножения и 12 сложений. А именно, воспользуемся равенством (12) и учтем, что в поле 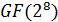 согласно второму из тождеств в (20) выполняется равенство
согласно второму из тождеств в (20) выполняется равенство 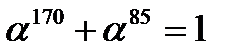 ,char
,char 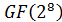 =2. Имеем:
=2. Имеем:
При табличной реализации умножения необходимо иметь только один массив длины 256 произведений всех элементов поля на элемент 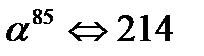 . Алгоритм:
. Алгоритм:
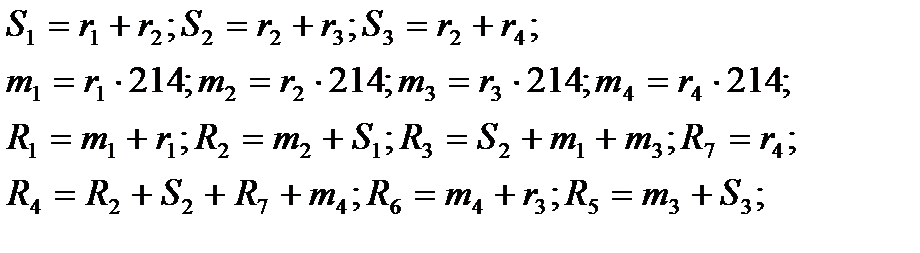 (22)
(22)
Для остальных 5 умножений вида R(x)=r(x)b(x) число умножений не уменьшается, равно 9, и алгоритм, согласно (12), можно записать в виде:
Алгоритм: 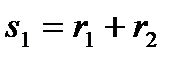 ,
, 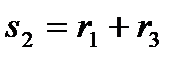 ,
, 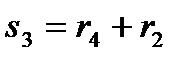 ,
, 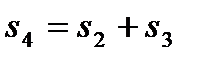 ,
, 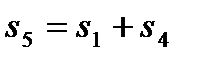 ,
, 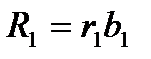 ,
,
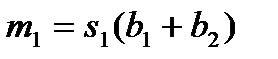 ,
, 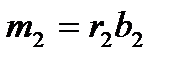 ,
, 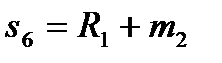 ,
, 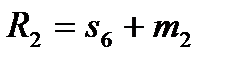 ,
, 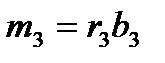 ,
, 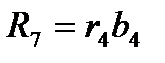 , (23)
, (23) 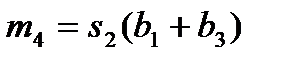 ,
, 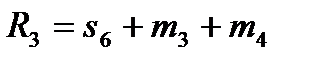 ,
, 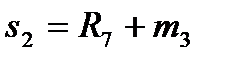 ,
, 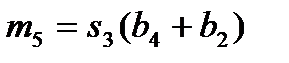 ,
, 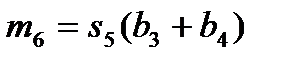 ,
, 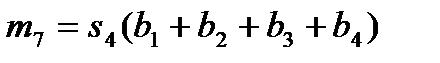 ,
, 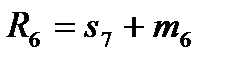 ,
,  ,
, 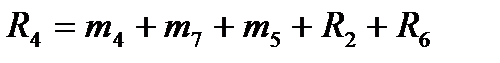 .
.
Так как суммы коэффициентов 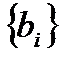 , естественно, вычисляются заранее и вводятся в алгоритм фиксированными константами, то всего имеем 9 умножений и 17 сложений. Для входящих в (20) коэффициентов, величины
, естественно, вычисляются заранее и вводятся в алгоритм фиксированными константами, то всего имеем 9 умножений и 17 сложений. Для входящих в (20) коэффициентов, величины
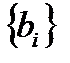 соответственно равны:
соответственно равны:
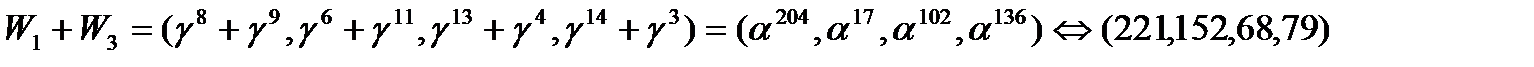
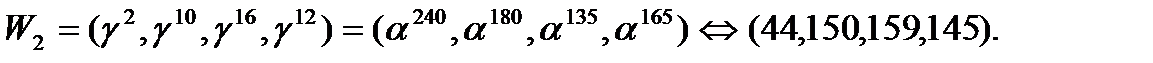
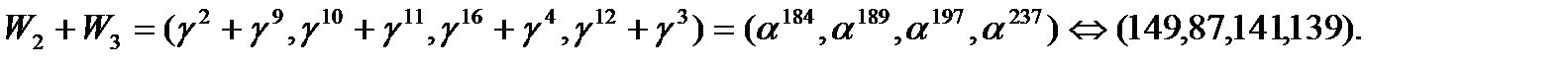
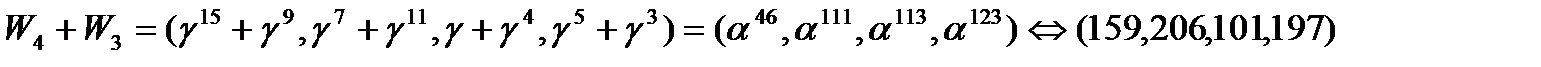
Полное число сложений и умножений для этой реализации равно соответственно 129 и 61. Для полного БПФ по длине 255 имеем 1935 сложений и 1255 умножений.



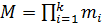 –произведение целых положительных попарно взаимно-простых положительных чисел, пусть
–произведение целых положительных попарно взаимно-простых положительных чисел, пусть 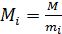 и пусть
и пусть 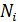 удовлетворяют равенству
удовлетворяют равенству 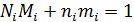 , тогда единственным решением системы сравнений
, тогда единственным решением системы сравнений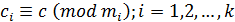
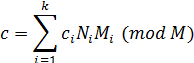
 , i=1,k.
, i=1,k.
 5
5 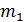 =3,
=3, 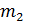 = 5,
= 5, 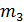 =17, так что n
=17, так что n 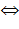 (
(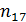 ,
, 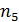 ,
, 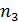 ), где
), где
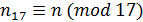 ,
,  ,
, 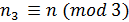
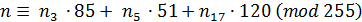
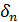 поля
поля 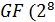 ) задается как степень примитивного элемента
) задается как степень примитивного элемента 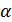 поля:
поля: 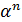 ,
, 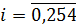
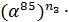 (
(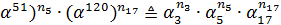 ,
,
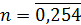 ,
,  ,
, 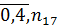 =
=  ,
,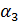 =
= 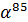 ,
, 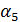 =
=  ,
, 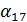 =
= 
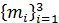 , если i
, если i 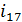 ,
, 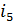 ,
, 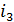 ) и j
) и j 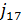 ,
, 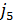 ,
,  ), то ij
), то ij 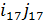 ,
, 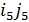 ,
, 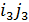 ). Таким образом, формулу (4.1) определяющую ДПФ, можно переписать в виде:
). Таким образом, формулу (4.1) определяющую ДПФ, можно переписать в виде: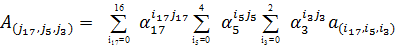
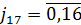 ,
,  ,
,  по вектору
по вектору 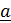 . Сначала разбиваем координаты вектора
. Сначала разбиваем координаты вектора 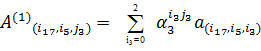
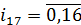 ,
, 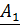 длины 255 применяется 5-точечное ДПФ с ядром
длины 255 применяется 5-точечное ДПФ с ядром 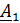 группируются по 5 чисел (по фиксированным
группируются по 5 чисел (по фиксированным 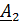 ,
,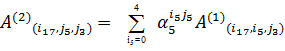
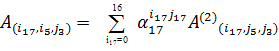
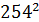 умножений при прямом вычислении по формуле (4.1) требует
умножений при прямом вычислении по формуле (4.1) требует
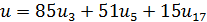
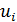 - число умножений, необходимое для выполнения i-точечного ДПФ, i=3,5,17. Аналогично выписывается и формула для числа сложений (кстати, напомним, что характеристика рассматриваемого поля равна 2, так что вычитание совпадает со сложением)
- число умножений, необходимое для выполнения i-точечного ДПФ, i=3,5,17. Аналогично выписывается и формула для числа сложений (кстати, напомним, что характеристика рассматриваемого поля равна 2, так что вычитание совпадает со сложением)
 задается формулой
задается формулой )=
)= 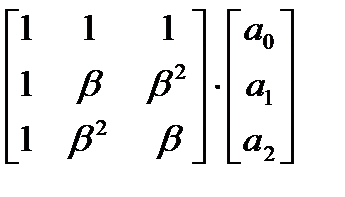
 , то легко проверить непосредственно, что числа
, то легко проверить непосредственно, что числа  могут быть вычислены по правилу:
могут быть вычислены по правилу: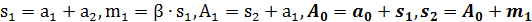
 , которое содержит только одно умножение и 5 сложений (вместо 4 умножений и 6 сложений). Если
, которое содержит только одно умножение и 5 сложений (вместо 4 умножений и 6 сложений). Если  ,
,  .
.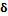 задается равенством
задается равенством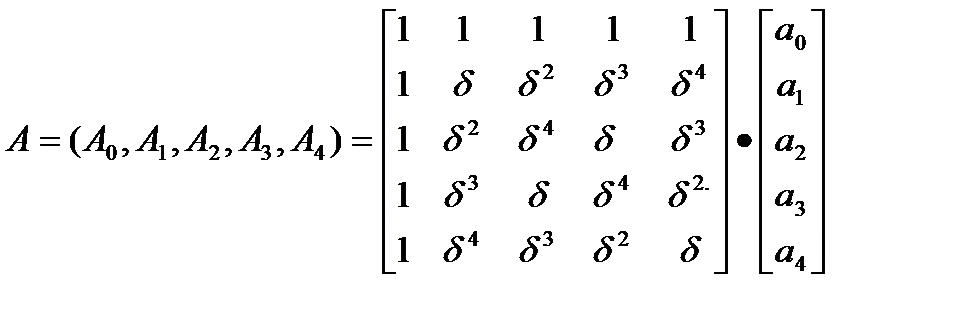 ,
,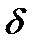 +
+ 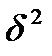 +
+ 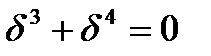 ) дает 9 умножений и 21 сложение. Это достигается, например, следующим образом:
) дает 9 умножений и 21 сложение. Это достигается, например, следующим образом: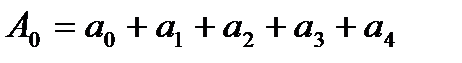 ,
,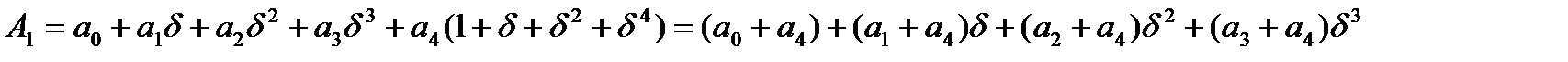 Аналогично,
Аналогично,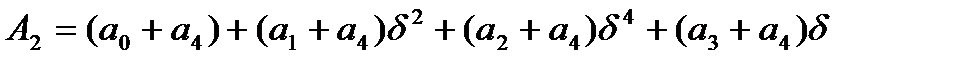 ,
,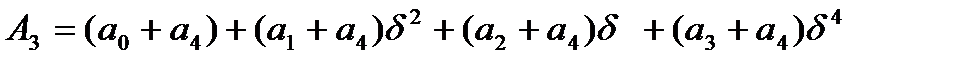 ,
,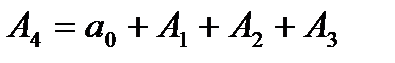
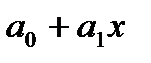 и
и 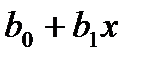 ,
, 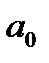 ,
, 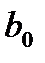 ,
, 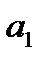 ,
,  , можно перемножить, выполняя не более трех умножений чисел в поле F.
, можно перемножить, выполняя не более трех умножений чисел в поле F.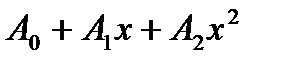 , где
, где  ,
, 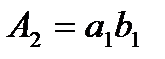 и
и 
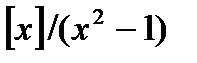 , то
, то  , где
, где 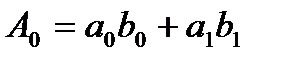 ,
, 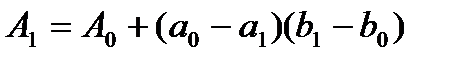
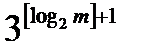 умножений чисел в поле F.
умножений чисел в поле F.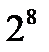 )=2) имеем:
)=2) имеем: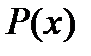 ≜
≜ 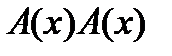 ≜
≜  =
=
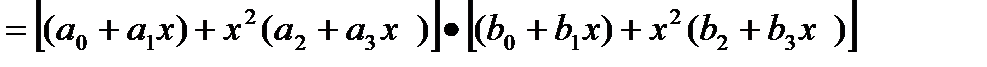 ≜
≜ 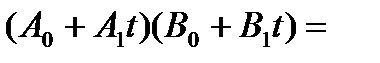
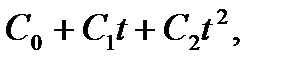
 (так что при вычислении по модулю многочлена
(так что при вычислении по модулю многочлена 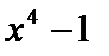 надо делать редукцию по модулю
надо делать редукцию по модулю  ); согласно утверждению 4.5.1:
); согласно утверждению 4.5.1: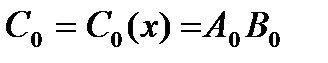 ≜
≜ 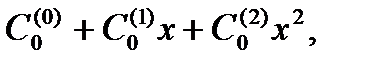
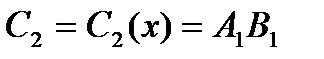 ≜
≜ 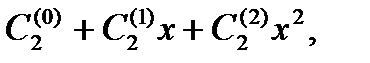
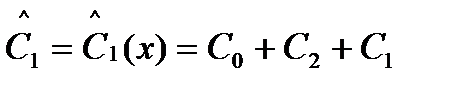
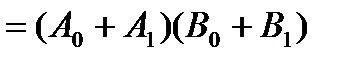 ≜
≜ 
 ,
, 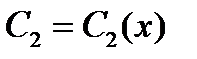 ,
, 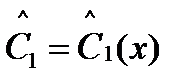 опять воспользуемся утверждением 4.5.1. Имеем
опять воспользуемся утверждением 4.5.1. Имеем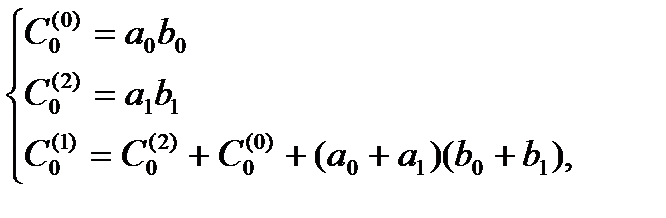
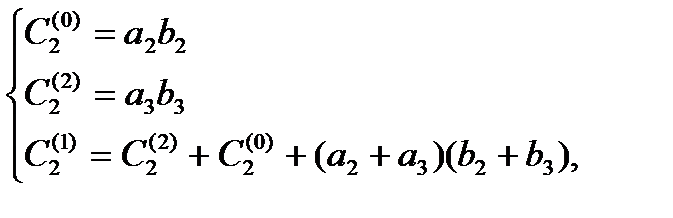
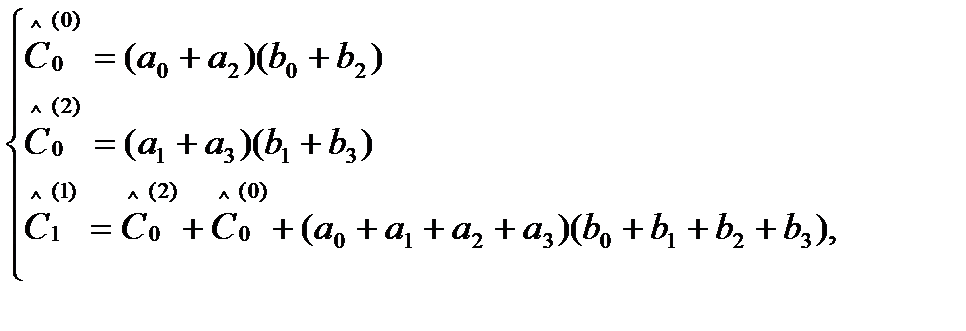
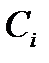 многочлена
многочлена  необходимо только 9 (вместо 16) умножений. Точные формулы для коэффициентов многочлена
необходимо только 9 (вместо 16) умножений. Точные формулы для коэффициентов многочлена 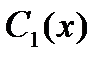 (при
(при 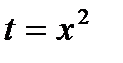 ) имеют вид:
) имеют вид:
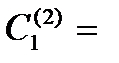
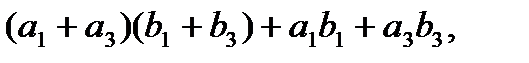
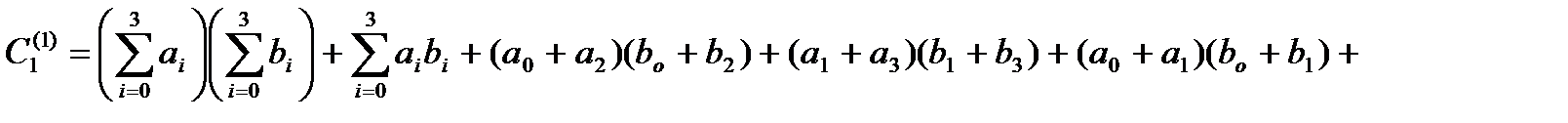
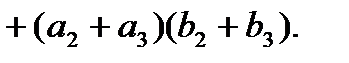
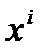 , согласно (10)-(12)
, согласно (10)-(12)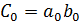 ,
,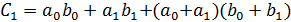 ,
,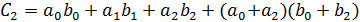 ,
,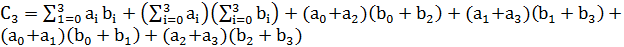 ,
,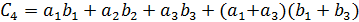 ,
,
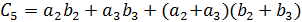 ,
,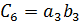 ,
,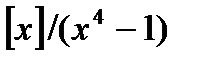 (так что
(так что 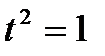 ), то формулы (10)-(12) принимают вид:
), то формулы (10)-(12) принимают вид: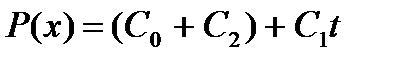 ≜
≜ 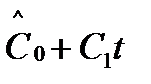 , (10а)
, (10а)
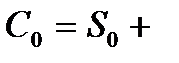
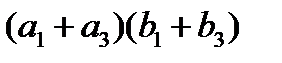 ,
,  ≜
≜ 
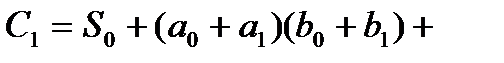
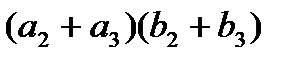 ,
,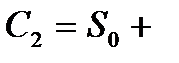
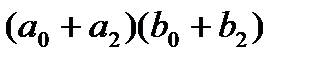
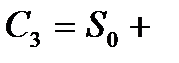
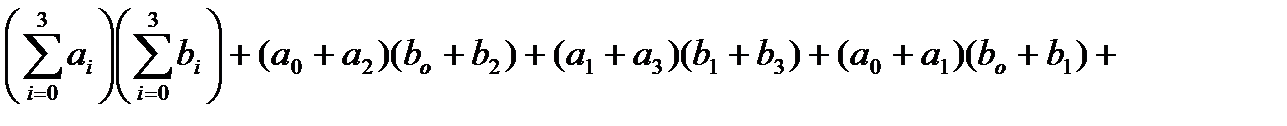
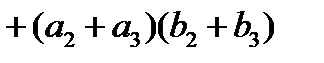 .
.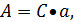 где
где 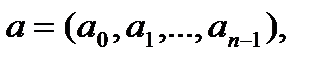 а
а 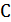 – циркулянт, первая строка которого задается вектором
– циркулянт, первая строка которого задается вектором 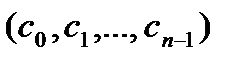 , равносильно вычислению в F
, равносильно вычислению в F 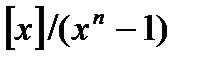 произведения
произведения 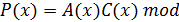
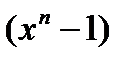 , где
, где 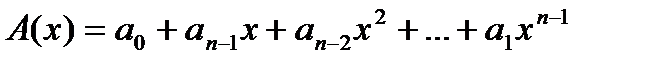 и
и 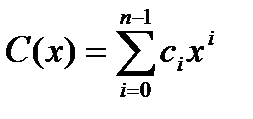 .
.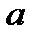 , за исключением первого элемента, дает реверсивный порядок коэффициентов многочлена
, за исключением первого элемента, дает реверсивный порядок коэффициентов многочлена 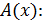 при
при 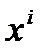 координате стоит коэффициент
координате стоит коэффициент 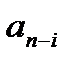 .
.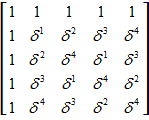

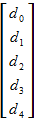 =
= 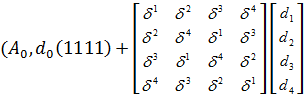 )
) .Если выполним такую же перестановку координат у векторов d и его спектра А, получаем
.Если выполним такую же перестановку координат у векторов d и его спектра А, получаем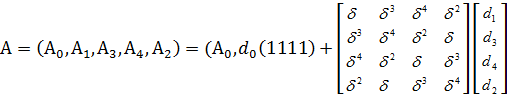 )
) 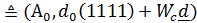 (14)
(14)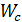 для БПФ длины 5 получается, если задать нумерацию ненулевого элемента поля GF (5) с образующей 3:
для БПФ длины 5 получается, если задать нумерацию ненулевого элемента поля GF (5) с образующей 3: 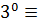 1 (mod5), 3
1 (mod5), 3 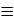 3 (mod5),
3 (mod5), 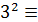 4 (mod5),
4 (mod5), 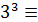 2 (mod5):
2 (mod5): 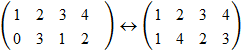 .
. -1), где d(x)=
-1), где d(x)= 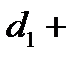
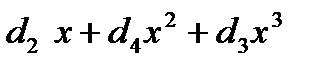 или, иначе, циклической свертки с=с
или, иначе, циклической свертки с=с 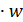
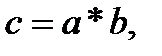
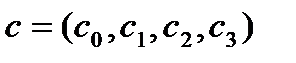 ,
, 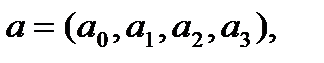
 ;
; (15)
(15)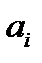 или
или 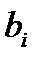 ,то число вычислений уменьшается. Например, если
,то число вычислений уменьшается. Например, если 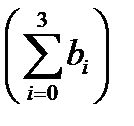 =0 или 1, то число умножений равно только 5. В нашем случае
=0 или 1, то число умножений равно только 5. В нашем случае 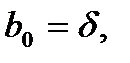
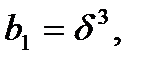
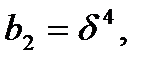
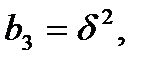 и так как
и так как 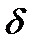 - ядро БПФ длины 5, то
- ядро БПФ длины 5, то 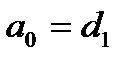 ,
, 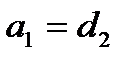 ,
, 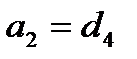 ,
, 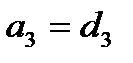 ,
, 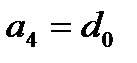 ,
, 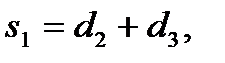
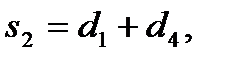
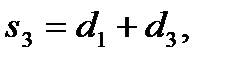
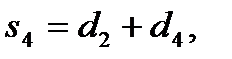
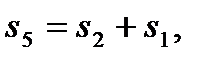
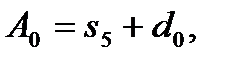
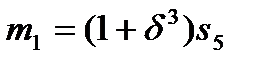 ,
, 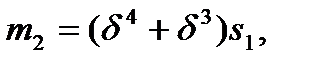
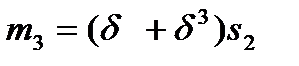 ,
, 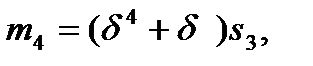
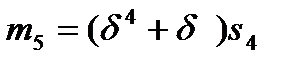 ,
, 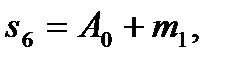
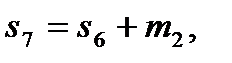
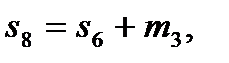

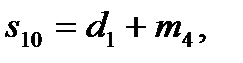
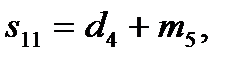

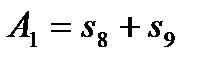 ,
,  ,
, 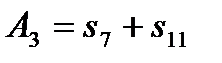 ,
, 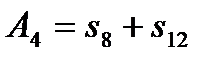 . (16)
. (16)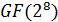 в нашем случае содержит 5 умножений и 11сложений.
в нашем случае содержит 5 умножений и 11сложений. 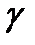 задается равенством
задается равенством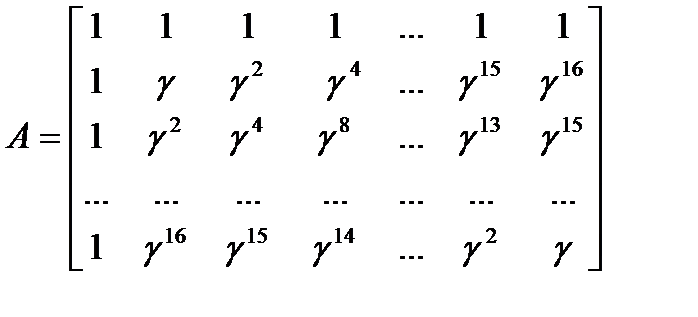
 (17)
(17)
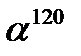 .
.
 соответственно имеет вид:
соответственно имеет вид: 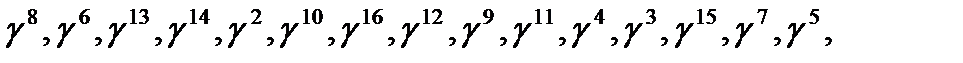
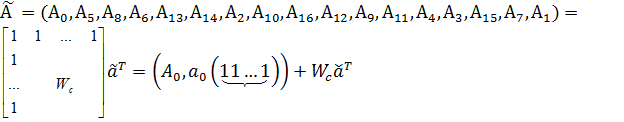 , (18)
, (18)
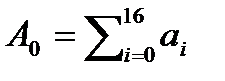 ,
, 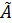 – вектор, полученный из спектра А указанной перестановкой координат, а
– вектор, полученный из спектра А указанной перестановкой координат, а 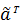 - вектор столбец, определяемый вторым равенством в (18).
- вектор столбец, определяемый вторым равенством в (18).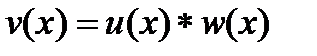
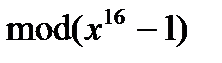 (19)
(19)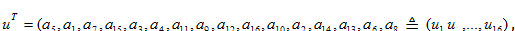
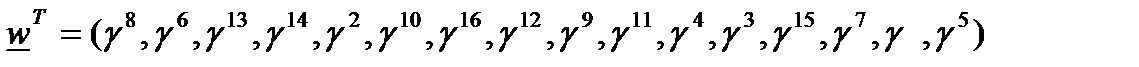
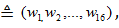
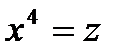 (так что
(так что 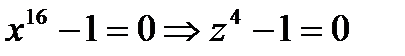 ) и пусть
) и пусть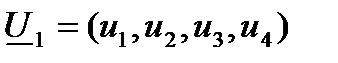
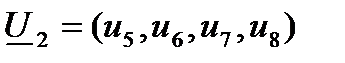
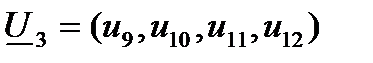
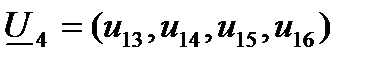
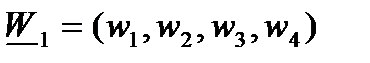
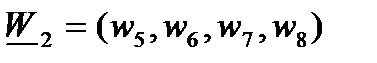
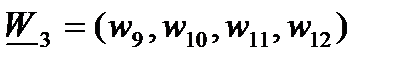

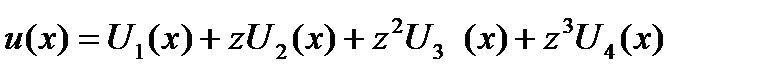
 ,
,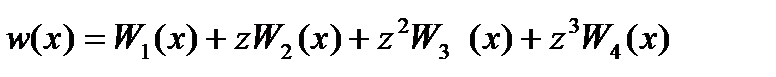
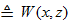 ,
,
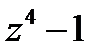 . Обозначая
. Обозначая 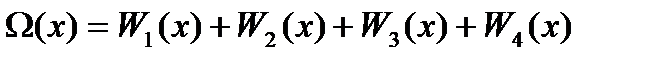 , согласно равенствам (15) имеем:
, согласно равенствам (15) имеем: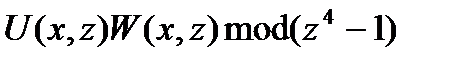
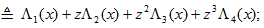
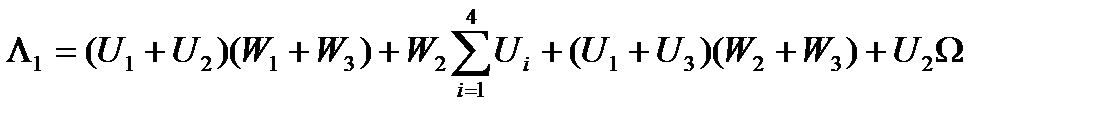
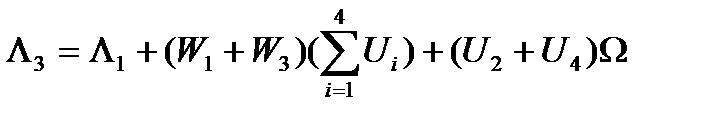 (20)
(20)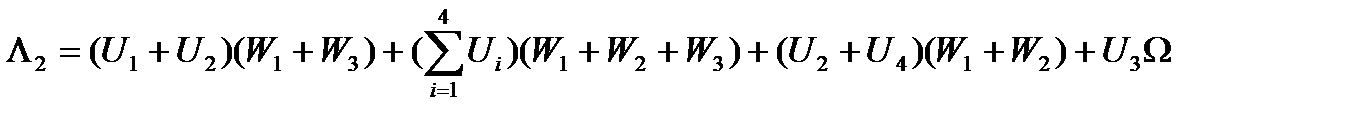
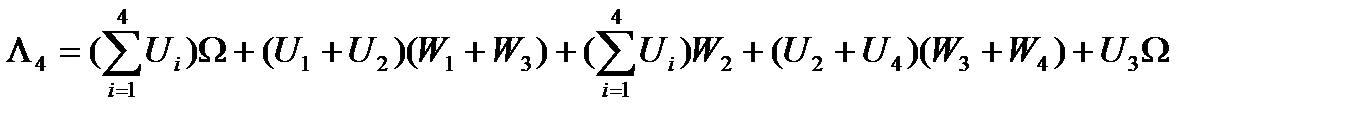
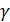 выполняется тождества:
выполняется тождества: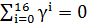 ;
;  ;
; 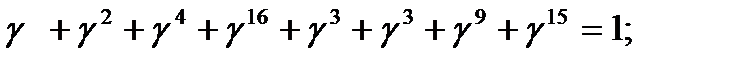
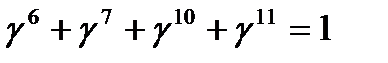 (21)
(21)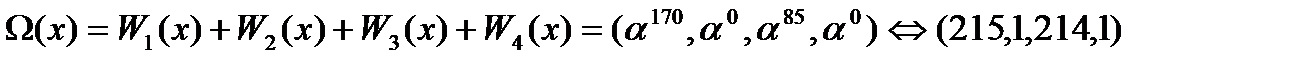
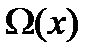 для произвольного многочлена
для произвольного многочлена 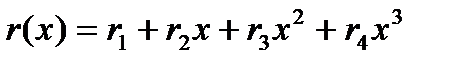 содержит 4 умножения и 12 сложений. А именно, воспользуемся равенством (12) и учтем, что в поле
содержит 4 умножения и 12 сложений. А именно, воспользуемся равенством (12) и учтем, что в поле 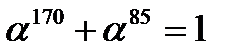 ,char
,char 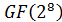 =2. Имеем:
=2. Имеем: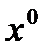
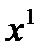
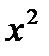
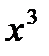


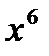
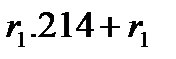
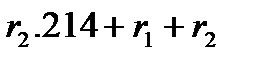
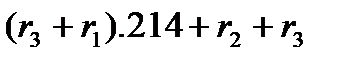

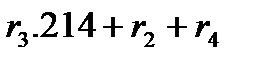
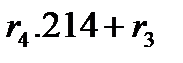

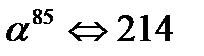 . Алгоритм:
. Алгоритм: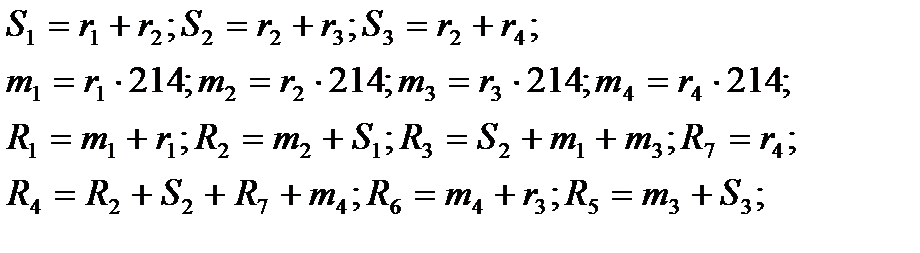 (22)
(22)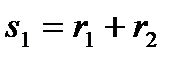 ,
, 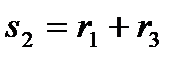 ,
, 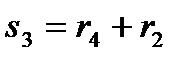 ,
, 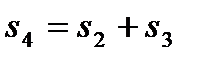 ,
, 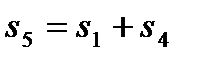 ,
, 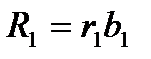 ,
,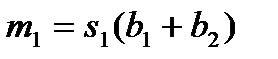 ,
, 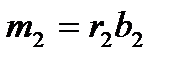 ,
, 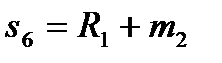 ,
, 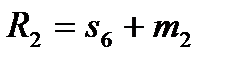 ,
, 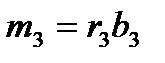 ,
, 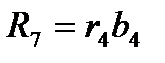 , (23)
, (23) 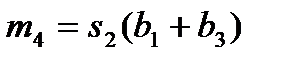 ,
, 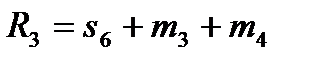 ,
, 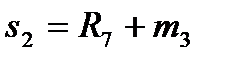 ,
, 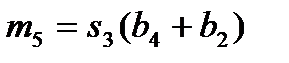 ,
, 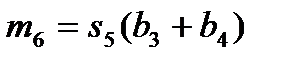 ,
, 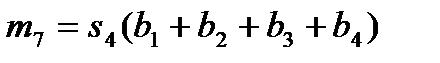 ,
, 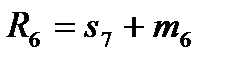 ,
,  ,
, 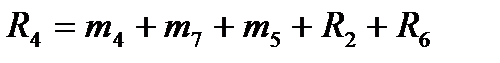 .
.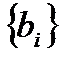 , естественно, вычисляются заранее и вводятся в алгоритм фиксированными константами, то всего имеем 9 умножений и 17 сложений. Для входящих в (20) коэффициентов, величины
, естественно, вычисляются заранее и вводятся в алгоритм фиксированными константами, то всего имеем 9 умножений и 17 сложений. Для входящих в (20) коэффициентов, величины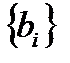 соответственно равны:
соответственно равны: