Количественная оценка стойкости парольной защиты

Пусть A – мощность алфавита паролей (количество символов, которые могут быть использованы при составлении пароля. Например, если пароль состоит только из малых английских букв, то A=26).

L – длина пароля.

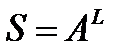- число всевозможных паролей длины L, которые можно составить из символов алфавита A.

V – скорость перебора паролей злоумышленником.

T – максимальный срок действия пароля.

Тогда, вероятность P подбора пароля злоумышленником в течении срока его действия V определяется по следующей формуле.

 

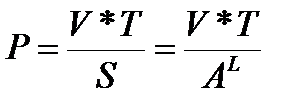
Задание к работе

1. Откройте программу генерации паролей, которая находится на сайте http://www.dinopass.com/

2. При помощи кнопки сгенерируйте 15 паролей различной длины и запишите их в тетрадь

3. Для каждого пароля рассчитать оценку стойкости парольной защиты по приведенной формуле с использованием таблицы (см. приложение 1), согласно своего варианта.

Контрольные вопросы

1. Чем определяется стойкость подсистемы идентификации и аутентификации?

2. Как определить вероятность подбора пароля злоумышленником в течении срока его действия?

3. Выбором каким параметров можно повлиять на уменьшение вероятности подбора пароля злоумышленником при заданной скорости подбора пароля злоумышленником и заданном сроке действия пароля?

Приложение 1.

Вариант	V	T
	15 паролей/мин	2 недели
	3 паролей/мин	10 дней
	10 паролей/мин	5 дней
	11 паролей/мин	6 дней
	100 паролей/день	12 дней
	10 паролей/день	1 месяц
	20 паролей/мин	3 недели
	15 паролей/мин	20 дней
	3 паролей/мин	15 дней
	10 паролей/мин	1 неделя
	11 паролей/мин	2 недели
	100 паролей/день	10 дней
	10 паролей/день	5 дней
	20 паролей/мин	6 дней
	15 паролей/мин	12 дней
	3 паролей/мин	1 месяц
	10 паролей/мин	3 недели
	11 паролей/мин	20 дней
	100 паролей/день	15 дней
	10 паролей/день	1 неделя
	20 паролей/мин	2 недели
	15 паролей/мин	10 дней
	3 паролей/мин	5 дней

 

 

Практическая работа №2

Тема: «Шифрование информации»

Цель работы: изучение простейших методов криптографической зашиты информации и закрепление навыков работы в программной среде Microsoft Excel.

Формируемые компетенции

ОК 1.	Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес
ОК 2.	Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество
ОК 3.	Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность
ОК 4.	Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития

План работы:

1. Изучение теоретического материала.

2. Зашифровывание своих фамилии и имени, используя метод Цезаря и среду Microsoft Excel.

3. Расшифровывание фразы с карточки, используя метод Цезаря и среду Microsoft Excel.

4. Зашифровать, расшифрованную в п.4 фразу методом перестановки с ключом. В качестве ключа взять свою фамилию.

5. Ответить устно на вопросы.

6. Предъявить работу преподавателю.

Теоретические сведения:

Система шифрования Цезаря – частный случай шифра простой замены. Метод основан на замене каждого символа сообщения (открытого текста) на другой символ того же алфавита, путем смещения от исходного на k позиций (получаем закрытый текст). Величина k называется ключом шифра (ключ – это информация, необходимая для беспрепятственного дешифрования информации). Ключ в методе Цезаря – целое число. Если поставить в соответствие каждому символу используемого алфавита число, то процесс шифрования будет проходить по формуле:

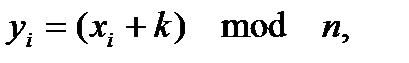
где x_i – номер i-того символа в открытом тексте, y_i – номер i-того символа в закрытом тексте, k – ключ, n – число символов в алфавите. Операция mod – это взятие остатка от деления одного числа на другое (например: 5 mod 2 = 1, 10 mod 5 = 0, 20 mod 7 = 6).

Дешифрование (расшифровывание) будет проходить по формуле

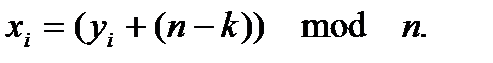
Пример.

Зашифруем методом Цезаря с ключом k=7 слово «шифр».

Будем использовать русский алфавит без буквы ё, где букве А соответствует число 0, а следовательно букве Я – 31. Т.е. n=32.

Поставим в исходном слове в соответствие каждой букве число:

ш	® 24	= х1
и	® 8	= х2
ф	® 20	= х3
р	® 16	= х4

Тогда y₁ = (x₁ + k) mod 32 = (24 +7) mod 32 = 31 mod 32 = 31 ® я

y₂ = (x₂ + k) mod 32 = (8 +7) mod 32 = 15 mod 32 = 15 ® п

y₃ = (x₃ + k) mod 32 = (20 +7) mod 32 = 27 mod 32 = 27 ® ы

y₄ = (x₄ + k) mod 32 = (16 +7) mod 32 = 23 mod 32 = 23 ® ч

Таким образом, получили слово «япыч»

Дешифрование.

Для дешифрования необходимо каждому символу слова «япыч» поставить в соответствие число:

я	® 31	= y1
п	® 15	= y2
ы	® 27	= y3
ч	® 23	= y4

Тогда x₁ = (y₁ + (32 – k)) mod 32 = (31 +(32 – 7)) mod 32 = 56 mod 32 = 24 ® ш

x₂ = (y₂ + (32 – k)) mod 32 = (15 +25) mod 32 = 40 mod 32 = 8 ® и

x₃ = (y₃ + (32 – k)) mod 32 = (27 +25) mod 32 = 52 mod 32 = 20 ® ф

x₄ = (y₄ + (32 – k)) mod 32 = (23 +25) mod 32 = 48 mod 32 = 16 ® р

Получили слово «шифр», следовательно шифрование было выполнено правильно.

Шифр перестановки с ключом – является одним из многочисленных видов шифров перестановки (символы исходного сообщения переставляются по определенным законам).

Для перестановки с ключом выбирается ключ – любое слово. Символы ключа нумеруется в порядке следования их в алфавите. Строится таблица, в которой количество столбцов равно количеству букв в ключе. Исходный текст вместе с пробелами и знаками препинания записывается в эту таблицу. Если последняя срока заполнена не полностью, до до конца строки записываются любые символы («пустышки»). Затем текст переписывается по столбцам, учитывая их нумерацию согласно ключу.

Пример.

Выберем в качестве ключа слово «информация». Пронумеруем ключ (первая, из имеющихся в ключе, в алфавите буква А, следовательно ей присваивается номер 1; следующая по алфавиту буква И, следовательно первая буква И будет иметь номер 2, а вторая – 3; далее идет буква М, ей присваиваем номер 4 и т.д.):

и	н	ф	о	р	м	а	ц	и	я

 

Зашифруем пословицу: От умного научишься, от глупого разучишься.

Запишем ее в таблицу под ключом. Оставшиеся ячейки до конца строки заполняют «пустышками».

 

и	н	ф	о	р	м	а	ц	и	я
о	т		у	м	н	о	г	о
н	а	у	ч	и	ш	ь	с	я	,
	о	т		г	л	у	п	о	г
о		р	а	з	у	ч	и	ш	ь
с	я	а	б	в	г	д	е	ж	з

Переписываем столбцы, учитывая их номер:

Оьучдон осояошжншлугтао яуч абмигзв утрагспие,гьз

Для дешифрования зашифрованный текст записывается в таблицу по столбцам, учитывая их номер.

 

Задание к работе.

1. Ознакомьтесь с теоретической частью практической работы.

2. Загрузите программу Microsoft Excel.

3. На первом листе электронной книги запишите в столбец А буквы русского алфавита. В столбце В – номер букв, в столбце С – опять буквы (такая запись будет необходима для использования функции ВПР).

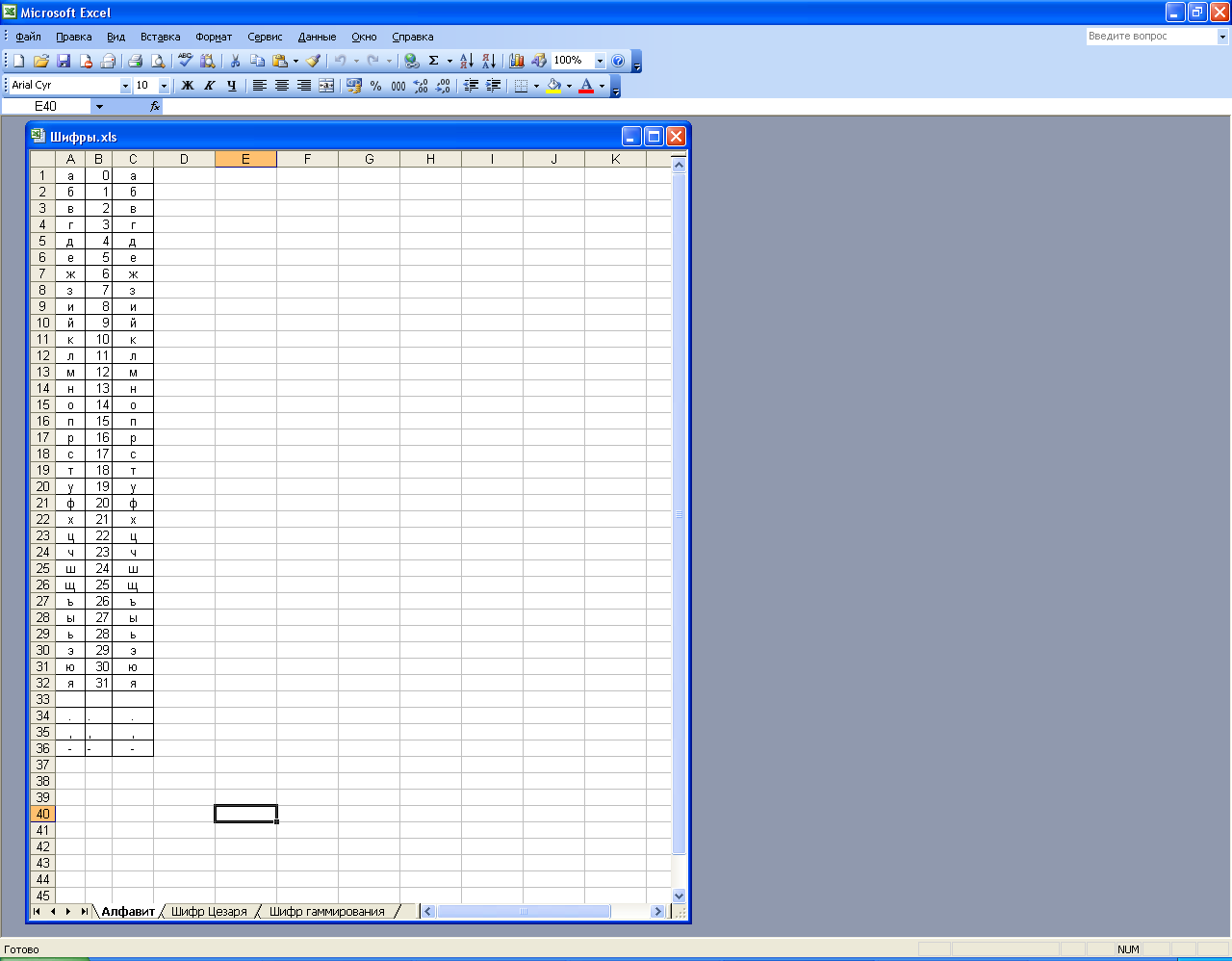
4. Переименуйте лист1 в Алфавит.

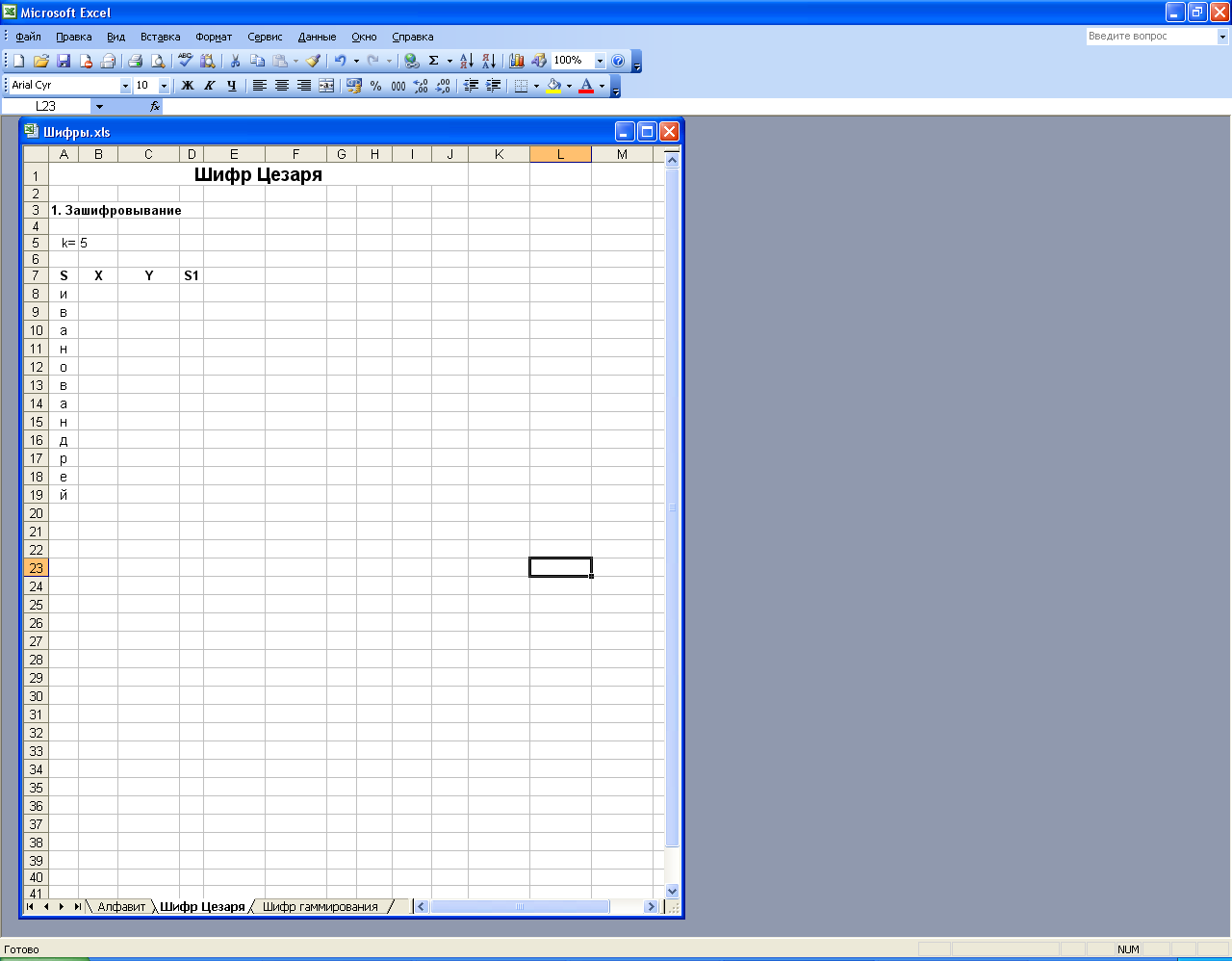
5. На втором листе электронной книги запишите название работы, ключ и название столбцов таблицы (S – исходные символы, Х – числа исходных символов, Y – пересчитанные по формуле значения, S1 – символы закрытого текста). Значение ключа можно взять любым и обязательно его значение записать в отдельную ячейку (В5). В столбец S, начиная с 8 строки, впишите фамилию и имя, каждую букву в отдельной ячейке.

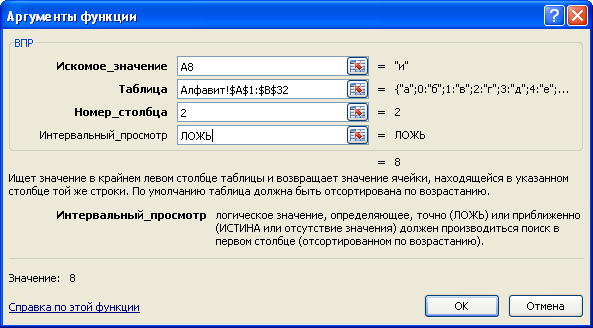
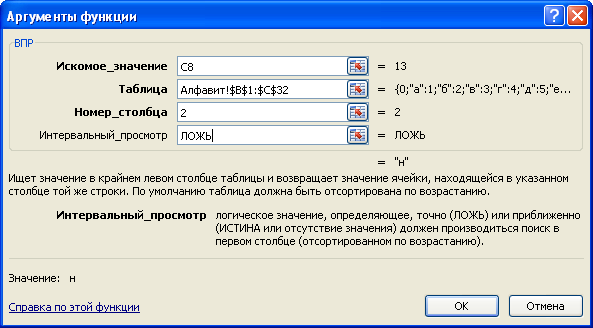
6. В столбце Х должны быть числовые значения символов из столбца S. Эти значения хранятся на листе Алфавит. Чтобы получить их, можно воспользоваться функцией ВПР (категория – ссылки и массивы). Встаем в ячейку В8 и вызываем функцию ВПР. Заполняем ее окно следующим образом:

7. Растянуть формулу вниз до конца таблицы.

8. В ячейку С8 (столбец Y) записывается формула для шифрования. Исходная формула метода Цезаря имеет вид: 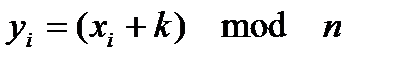.Операции mod в Excel соответствует функция ОСТАТ(число; делитель). В нашем случае число – это 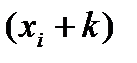, а делитель – 32. Т.е. функция ОСТАТ будет иметь вид =ОСТАТ((B8+$B$5);32).

9. Эту формулу необходимо растянуть вниз до конца таблицы.

10. В ячейку D8 (столбец S1) опять записываем функцию ВПР, которая по числу Y найдет букву. Эта функция будет выглядеть следующим образом:

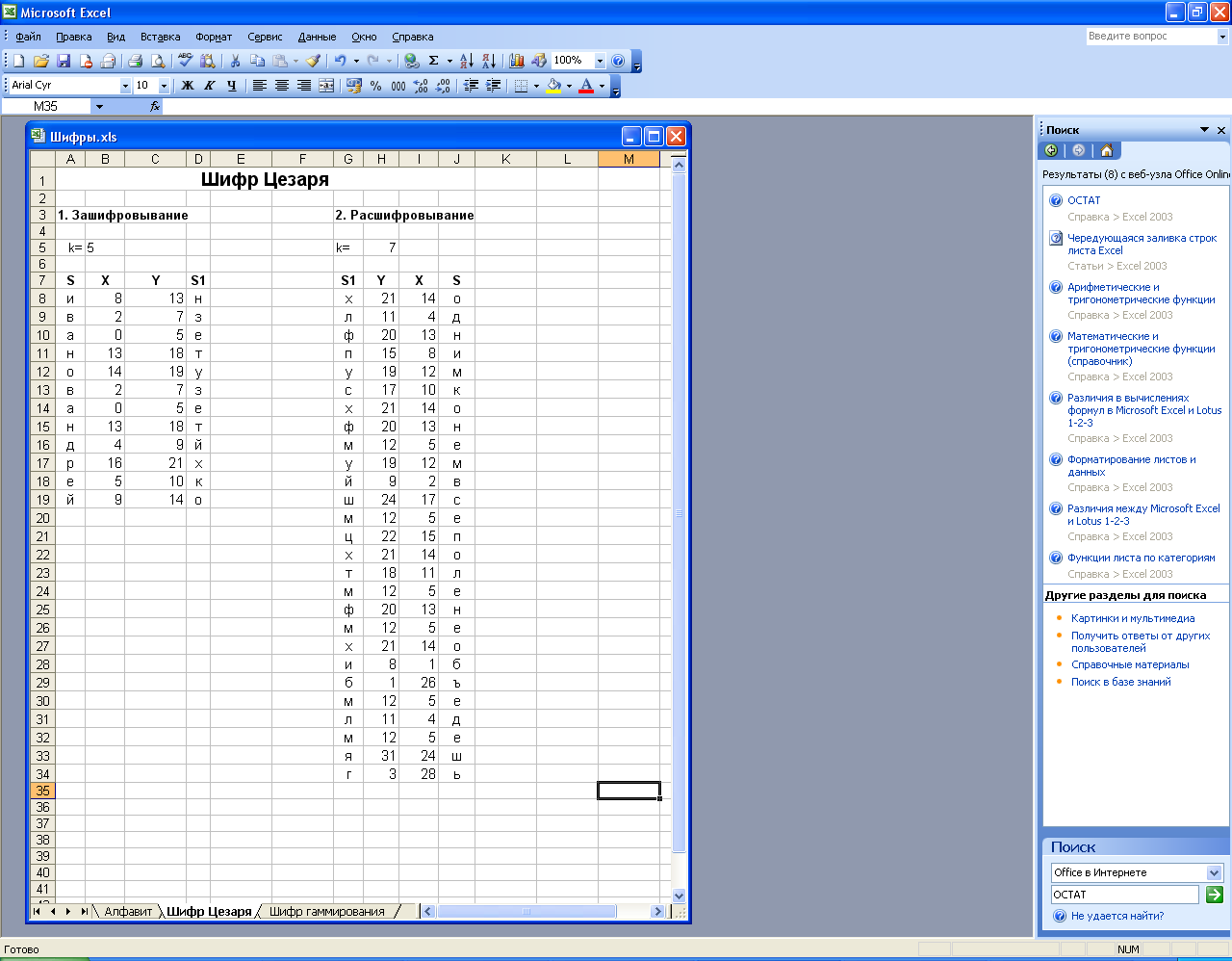
11. Окончательно таблица должна выглядеть следующим образом:

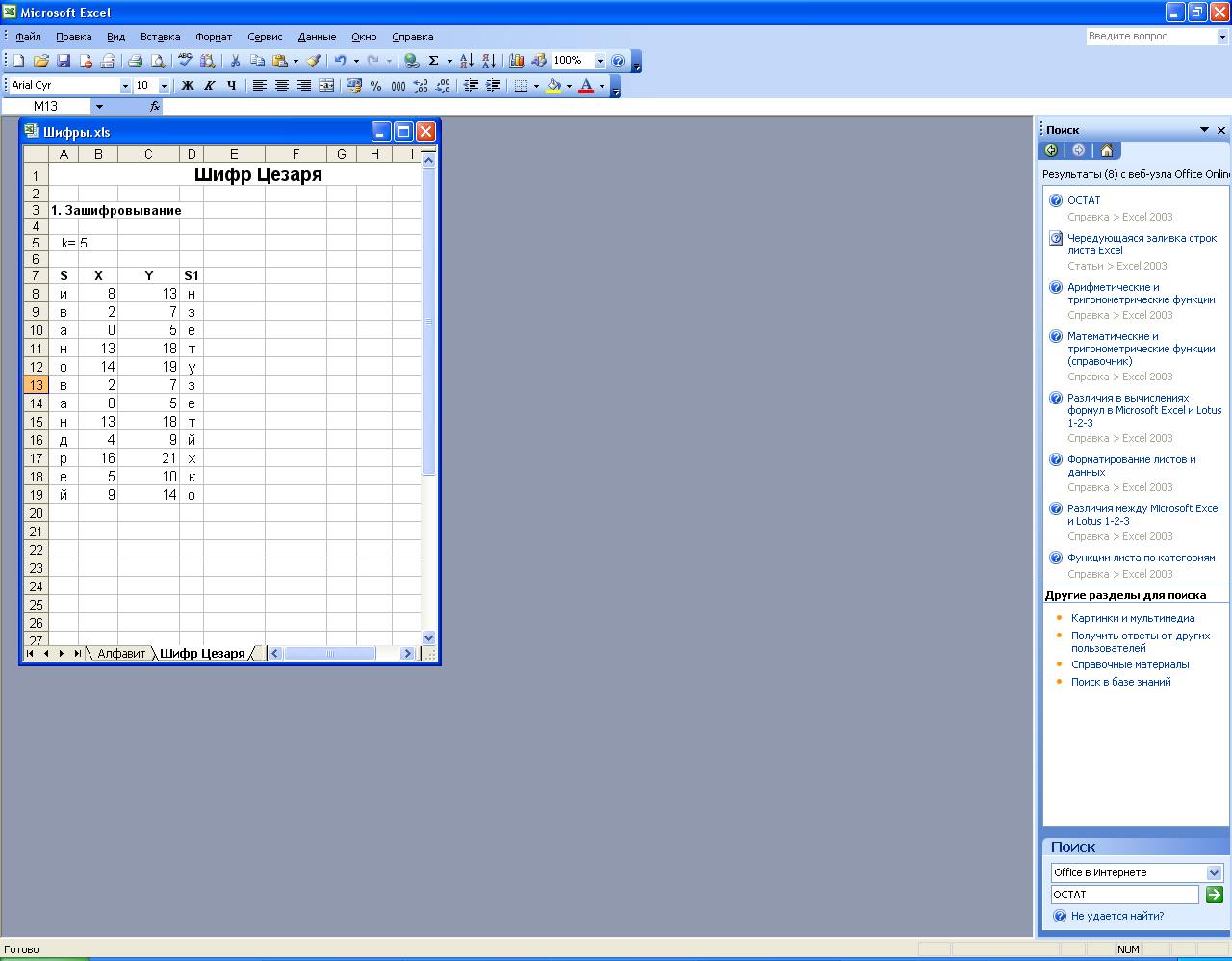
Запишите полученный закрытый текст (столбец S1) в тетрадь.

12. Рядом приготовьте место для дешифрования информации. Получите у преподавателя карточку с закрытым текстом и впишите его в столбец S1 новой таблицы.

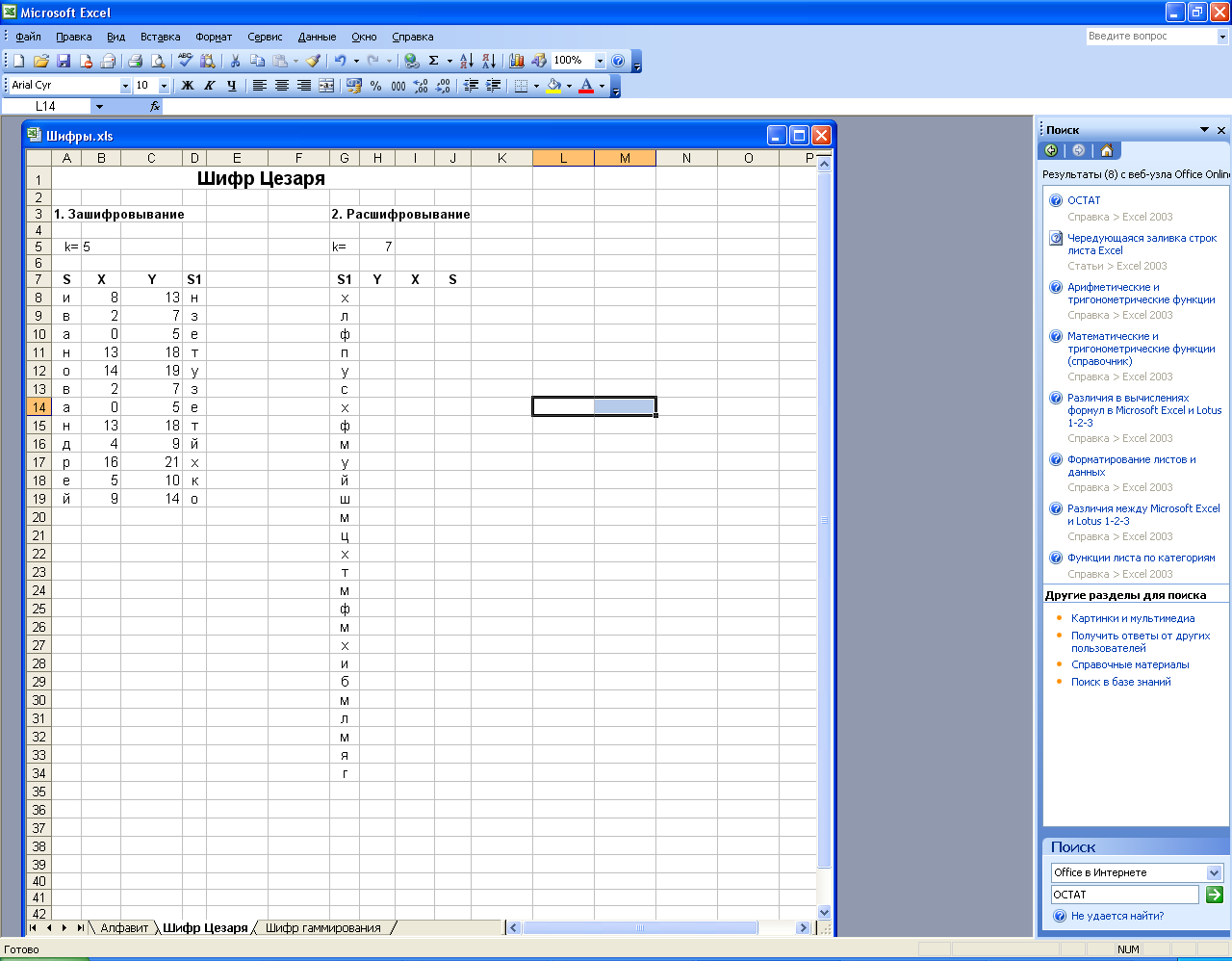
13. Проведите дешифрования текста по аналогии с зашифровыванием. Для расшифровывания (столбца Х) используйте формулу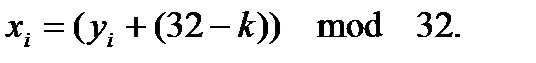

14. Запишите полученную фразу в тетрадь.

15. Зашифруйте в тетради расшифрованную фразу методом перестановки с ключом. В качестве ключа используйте свою фамилию.

16. Предъявите работу преподавателю.

 

Контрольные вопросы.

1. Какой текст называется открытым?

2. Какой текст называется закрытым?

3. Что такое ключ?

4. Как осуществляется процесс шифрования в методе Цезаря?

5. Что такое «шифрование методом перестановки»?

6. Как работает функция ОСТАТ?

7. Что делает функция ВПР?

 

Варианты заданий

№1 Используя ключ 8 проведите дешифрование информации, зашифрованной методом Цезаря: фищтршцкти - еъц эръшцщъд р щхцшцкти	№2 Используя ключ 6 проведите дешифрование информации, зашифрованной методом Цезаря: ршф ыфэлш туфйф нужшв, шфтщ ужкф тжсф чхжшв
№3 Используя ключ 4 проведите дешифрование информации, зашифрованной методом Цезаря: уфйичуфйимца жтжфйрг - ийпт ифчлйн	№4 Используя ключ 6 проведите дешифрование информации, зашифрованной методом Цезаря: ифнвтлшче ужцфк - фнлцф хлцлсвлш
№5 Используя ключ 7 проведите дешифрование информации, зашифрованной методом Цезаря: хлфпу схфму йшм цхтм фм хибмлмяг	№6 Используя ключ 9 проведите дешифрование информации, зашифрованной методом Цезаря: мно ъфчлй щонус, ыйх чцс лоъ схозы
№7 Используя ключ 10 проведите дешифрование информации, зашифрованной методом Цезаря: цкх йсеф, ок мыпц ьпхшц мхкоппь	№8 Используя ключ 7 проведите дешифрование информации, зашифрованной методом Цезаря: юму ихтгям фзъсп, щму ъуфмм чъсп
№9 Используя ключ 9 проведите дешифрование информации, зашифрованной методом Цезаря: хйфч нсшфчх схоые, цйнч нофч щйрьхоые	№10 Используя ключ 4 проведите дешифрование информации, зашифрованной методом Цезаря: рчифтхца - сдмрйсаьдг цгкйпдг стьд ж учцм
№11 Используя ключ 10 проведите дешифрование информации, зашифрованной методом Цезаря: щъшнэхжчеп очт мшъшмыьмэ ыъшочт	№12 Используя ключ 5 проведите дешифрование информации, зашифрованной методом Цезаря: уч ирем чурпш серу, кцрн шс цркф
№13 Используя ключ 6 проведите дешифрование информации, зашифрованной методом Цезаря: рфтщ цжзфшж и шейфчшв, шфтщ ул илкфтж	№14 Используя ключ 7 проведите дешифрование информации, зашифрованной методом Цезаря: ьхчхямм йхшцпщзфпм - тъюямм фзштмлшщйх
№15 Используя ключ 8 проведите дешифрование информации, зашифрованной методом Цезаря: чцфиэинад тцщцс - йымнъ щуимцт чцтцс	№16 Используя ключ 9 проведите дешифрование информации, зашифрованной методом Цезаря: уыч хцчмч цйасцйоы, ычы хйфч учцайоы

 

 

Практическая работа №3

Тема: Изучение методов шифрования. Шифры замены и шифры перестановки.

 

Цель работы: Научится применять шифры замены и шифры перестановки для шифрования данных.

Формируемые компетенции

ОК 1.	Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес
ОК 2.	Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество
ОК 3.	Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность
ОК 4.	Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития

Порядок выполнения работы.

 

1. Записать в тетради тему и цель работы.

2. Ознакомится с теоретическими сведениями.

3. Выполнить задания

4. Оформить отчет

 

Теоретические сведения.

Шифры замены

1. Полибианский квадрат. Шифр изобретен греческим государственным деятелем, полководцем и историком Полибием (III век до н.э.). Применительно к русскому алфавиту суть шифрования заключалась в следующем. В квадрат 6х6 выписываются буквы.

Рис.1. Таблица шифрозамен для полибианского квадрата

 

Шифруемая буква заменяется на координаты квадрата (строка-столбец), в котором она записана. Например, если исходное сообщение «АБРАМОВ», то шифрограмма – «11 12 36 11 32 34 13». В Древней Греции сообщения передавались с помощью оптического телеграфа (с помощью факелов). Для каждой буквы сообщения в начале поднималось количество факелов, соответствующее номеру строки буквы, а затем номеру столбца.

2. Шифрующая система Трисемуса (Тритемия). В 1508 г. аббат из Германии Иоганн Трисемус написал печатную работу по криптологии под названием «Полиграфия». В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. На рис.6 изображена таблица с ключевым словом «ДЯДИНА».

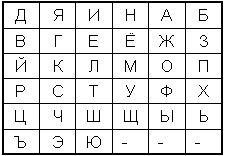
Рис.2. Таблица шифрозамен для шифра Трисемуса

 

Каждая буква открытого сообщения заменяется буквой, расположенной под ней в том же столбце. Если буква находится в последней строке таблицы, то для ее шифрования берут самую верхнюю букву столбца. Например, исходное сообщение «АБРАМОВ», зашифрованное – «ЖЗЦЖУФЙ».

Полиграммные шифры замены - шифры, которые шифруют сразу группы (блоки) символов.

3. Шифр Playfair (англ. «Честная игра»). Был изобретен в 1854 г. Чарльзом Уитстоном, но назван именем лорда Лайона Плейфера, который внедрил данный шифр в государственные службы Великобритании. Он использовался англичанами в Первой мировой войне. Шифр предусматривает шифрование пар символов (биграмм). Таким образом, этот шифр более устойчив к взлому по сравнению с шифром простой замены, так как затрудняется частотный анализ. Он может быть проведен, но не для 26 возможных символов (латинский алфавит), а для 26 х 26 = 676 возможных биграмм. Анализ частоты биграмм возможен, но является значительно более трудным и требует намного большего объема зашифрованного текста.

Для шифрования сообщения необходимо разбить его на биграммы (группы из двух символов), при этом, если в биграмме встретятся два одинаковых символа, то между ними добавляется заранее оговоренный вспомогательный символ (в оригинале – X, для русского алфавита - Я). Например, «зашифрованное сообщение» становится «за ши фр ов ан но ес о Я об ще ни е Я». Для формирования ключевой таблицы выбирается лозунг и далее она заполняется по правилам шифрующей системы Трисемуса. Например, лозунг «ДЯДИНА»

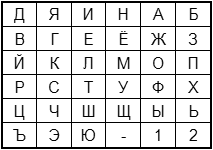
Рис.3. Ключевая таблица для шифра Playfair

 

Затем, руководствуясь следующими правилами, выполняется зашифровывание пар символов исходного текста:

1. Если символы биграммы исходного текста встречаются в одной строке, то эти символы замещаются на символы, расположенные в ближайших столбцах справа от соответствующих символов. Если символ является последним в строке, то он заменяется на первый символ этой же строки.

2. Если символы биграммы исходного текста встречаются в одном столбце, то они преобразуются в символы того же столбца, находящимися непосредственно под ними. Если символ является нижним в столбце, то он заменяется на первый символ этого же столбца.

3. Если символы биграммы исходного текста находятся в разных столбцах и разных строках, то они заменяются на символы, находящиеся в тех же строках, но соответствующие другим углам прямоугольника.

Пример шифрования.

- биграмма «за» формирует прямоугольник – заменяется на «жб»;

- биграмма «ши» находятся в одном столбце – заменяется на «юе»;

- биграмма «фр» находятся в одной строке – заменяется на «хс»;

- биграмма «ов» формирует прямоугольник – заменяется на «йж»;

- биграмма «ан» находятся в одной строке – заменяется на «ба»;

- биграмма «но» формирует прямоугольник – заменяется на «ам»;

- биграмма «ес» формирует прямоугольник – заменяется на «гт»;

- биграмма «оя» формирует прямоугольник – заменяется на «ка»;

- биграмма «об» формирует прямоугольник – заменяется на «па»;

- биграмма «ще» формирует прямоугольник – заменяется на «шё»;

- биграмма «ни» формирует прямоугольник – заменяется на «ан»;

- биграмма «ея» формирует прямоугольник – заменяется на «ги».

Шифрограмма – «жб юе хс йж ба ам гт ка па шё ан ги».

Для расшифровки необходимо использовать инверсию этих правил, откидывая символы Я (или Х), если они не несут смысла в исходном сообщении.

Полиалфавитные шифры.

4. Таблица Трисемуса. Одним из шифров, придуманных немецким аббатом Трисемусом, стал многоалфавитный шифр, основанный на так называемой «таблице Трисемуса» - таблице со стороной равной n, где n – количество символов в алфавите. В первой строке матрицы записываются буквы в порядке их очередности в алфавите, во второй – та же последовательность букв, но с циклическим сдвигом на одну позицию влево, в третьей – с циклическим сдвигом на две позиции влево и т.д.

Рис.4. Таблица Трисемуса

 

Здесь первая строка является одновременно и строкой букв открытого текста. Первая буква текста шифруется по первой строке, вторая буква по второй и так далее после использования последней строки вновь возвращаются к первой. Так сообщение «АБРАМОВ» приобретет вид «АВТГРУИ».

5. Система шифрования Виженера. В 1586 г. французский дипломат Блез Виженер представил перед комиссией Генриха III описание простого, но довольно стойкого шифра, в основе которого лежит таблица Трисемуса.

Перед шифрованием выбирается ключ из символов алфавита. Сама процедура шифрования заключается в следующем. По i-ому символу открытого сообщения в первой строке определяется столбец, а по i-ому символу ключа в крайнем левом столбце – строка. На пересечении строки и столбца будет находиться i-ый символ, помещаемый в шифрограмму. Если длина ключа меньше сообщения, то он используется повторно. Например, исходное сообщение «АБРАМОВ», ключ – «ДЯДИНА», шифрограмма – «ДАФИЩОЖ».

Справедливости ради, следует отметить, что авторство данного шифра принадлежит итальянцу Джованни Батиста Беллазо, который описал его в 1553 г. История «проигнорировала важный факт и назвала шифр именем Виженера, несмотря на то, что он ничего не сделал для его создания». Беллазо предложил называть секретное слово или фразу паролем (ит. password; фр. parole - слово).

Шифры перестановки

6. Шифр блочной одинарной перестановки. При использовании этого шифра задается таблица перестановки блока символов, которая последовательно применяется до тех пор, пока исходное сообщение не закончится. Если исходное сообщение не кратно размеру блока, тогда оно при шифровании дополняется произвольными символами.

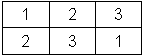
Рис.5. Таблица перестановок

 

Для примера выберем размер блока, равный 3, и примем таблицу перестановок, показанную на рис.5. Дополним исходное сообщение «АБРАМОВ» буквами Ь и Э, чтобы его длина была кратна 3. В результате шифрования получим «РАБОАМЭВЬ».

Количество ключей для данного шифра при фиксированном размере блока равно m!, где m – размер блока.

7. Шифр табличной маршрутной перестановки. Наибольшее распространение получили шифры маршрутной перестановки, основанные на таблицах. При шифровании в такую таблицу вписывают исходное сообщение по определенному маршруту, а выписывают (получают шифрограмму) - по другому. Для данного шифра маршруты вписывания и выписывания, а также размеры таблицы являются ключом.

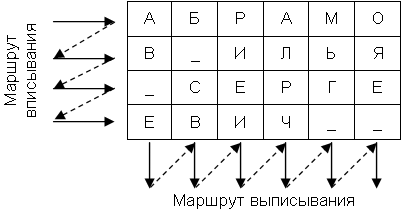
Рис. 6.. Пример использования шифра маршрутной перестановки

 

Например, исходное сообщения «АБРАМОВ ИЛЬЯ СЕРГЕЕВИЧ» вписывается в прямоугольную таблицу размерами 4х6, маршрут вписывания – слева-направо сверху-вниз, маршрут выписывания – сверху-вниз слева-направо. Шифрограмма в этом случае выглядит «АВ_ЕБ_СВРИЕИАЛР ЧМЬГ_ОЯЕ_».

8. Шифры с использованием треугольников и трапеций. Помочь выполнить перестановки могут как треугольники, так и трапеции. Открытый текст вписывается в эти фигуры в соответствии с количеством слов и формой выбранной фигуры, которая может быть растянута или сжата, чтобы в ней поместилось сообщение. Для первой фигуры, треугольника, открытый текст записывается построчно от вершины до основания.

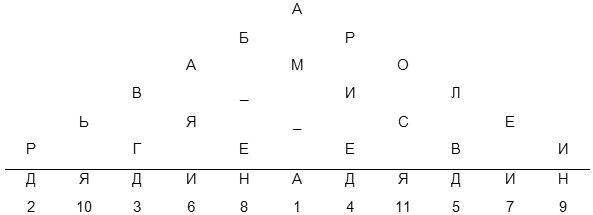
Рис.7. Пример использования шифра перестановки при вписывании в треугольник

 

Ниже записывается ключевое слово. Поскольку основание широкое, ключевое слово повторяется. Буквы строки с ключевым словом нумеруются последовательно согласно их алфавитному порядку. Зашифрованное сообщение выписывается по столбцам согласно выполненной нумерации. Таким образом, для открытого текста «АБРАМОВ ИЛЬЯ СЕРГЕЕВИ» и ключевого слова «ДЯДИНА» шифрограмма будет выглядеть «АМ_РВГРИЕЛВАЯЕБ_ЕИЬРС».

9. Магические квадраты. Магическими квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами начиная с 1, которые в сумме по каждому столбцу, каждой строке и каждой диагонали дают одно и то же число. Подобные квадраты широко применялись для вписывания шифруемого текста по приведенной в них нумерации. Если потом выписать содержимое таблицы по строкам, то получалась шифровка перестановкой букв. На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата. Так, существует лишь один магический квадрат размером 3х3, если не принимать во внимание его повороты. Магических квадратов 4х4 насчитывается уже 880, а число магических квадратов размером 5х5 около 250000. Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени, потому что ручной перебор всех вариантов ключа для этого шифра был немыслим.

Рассмотри квадрат размером 4х4. В него вписываются числа от 1 до 16. Его магия состоит в том, что сумма чисел по строкам, столбцам и полным диагоналям равняется одному и тому же числу — 34. Впервые эти квадраты появились в Китае, где им и была приписана некоторая «магическая сила».

 

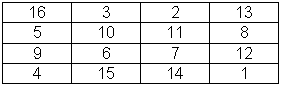
Рис.8. Магический квадрат 4х4

 

Шифрование по магическому квадрату производилось следующим образом. Например, требуется зашифровать фразу: «АБРАМОВДЯДИНА...». Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам: позиция буквы в предложении соответствует порядковому числу. В пустые клетки ставится точка или любая буква.

 

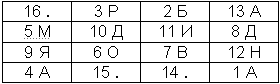
Рис.9. Пример шифрования с помощью магического квадрата

 

После этого шифрованный текст записывается в строку (считывание производится слева-направо сверху-вниз, построчно) – «.РБАМДИДЯОВНА..А».

10. Шифр двойной перестановки. В таблицу по определенному маршруту записывается текст сообщения, затем переставляются столбцы, а потом переставляются строки. Шифрограмма выписывается по определенному маршруту.

Пример шифрования сообщения «АБРАМОВ+ДЯДИНА» показан на рис.10. Результат шифрования – «ОАБЯ+_АИВ_РДМНАД».

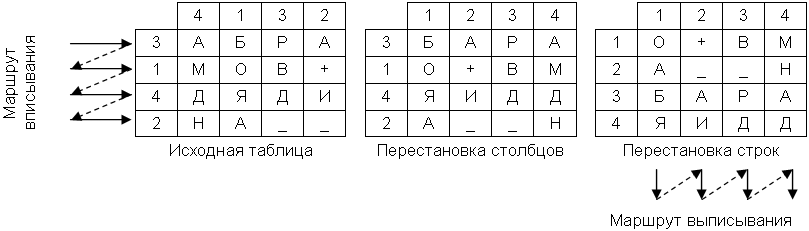
Рис.10. Пример использования шифра двойной перестановки

 

Ключом к шифру являются размеры таблицы, маршруты вписывания и выписывания, а также порядки перестановки столбцов и строк. Если маршруты являются фиксированными величинами, то количество ключей равно n!*m!, n и m – количество столбцов и строк в таблице.

Задания к работе

1. Необходимо зашифровать свою фамилию с помощью следующих шифров:

· полибианского квадрата;

· шифрующей системы Трисемуса;

· шифра Playfair

· таблицы Трисемуса.

· шифра Виженера.

· блочной одинарной перестановки;

3. Необходимо зашифровать фамилию и имя с помощью следующих шифров:

· табличной маршрутной перестановки;

· шифры с использованием треугольника.

· магический квадрат (размер квадрата - 4х4);

· двойной перестановки.

При оформлении отчета необходимо привести исходное сообщение (фамилию или фамилию и имя), таблицы, ключевые слова (выбираются произвольно), маршруты вписывания и выписывания, зашифрованное сообщение.

 

Практическая работа № 4