

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Колебания однородной бесконечной струны.
Формула Даламбера
Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с более простой задачи – задачи о свободных колебаниях однородной бесконечной струны. Это задача, как было показано в п. 1.24, сводится к решению уравнения

| (1.121) |
при начальных условиях
 , ,  , ,
| (1.122) |
где функции 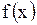 и
и 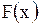 заданы на всей числовой оси. Никакие граничные условия на искомую функцию
заданы на всей числовой оси. Никакие граничные условия на искомую функцию 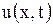 не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши.
не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши.
Для решения поставленной задачи преобразуем уравнение (1.121) к каноническому виду, содержащему смешанную производную (см. (1.93)). Для чего составим уравнение характеристик
 ,
,
которое распадается на два уравнения:
 и
и  .
.
Интегрируя эти уравнения, получим
 и
и  .
.
Согласно общей теории о замене переменных полагаем
 ,
,  .
.
Тогда уравнение (1.121) преобразуется к виду
 .
.
Как было показано в п.1.18 (см. формулу (1.87)), общее решение такого уравнения имеет вид
 ,
,
где  и
и  - произвольные функции. Возвращаясь к старым переменным
- произвольные функции. Возвращаясь к старым переменным 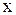 и
и 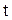 , получим общее решение волнового уравнения (1.121)
, получим общее решение волнового уравнения (1.121)
 . .
| (1.123) |
Определим функции  и
и 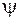 таким образом, чтобы удовлетворялись начальные условия (1.122)
таким образом, чтобы удовлетворялись начальные условия (1.122)
 ,
,
 .
.
Интегрируя последнее равенство по  , получим
, получим
 , где
, где 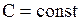 .
.
Из равенств
 ,
,

находим
 , ,
| (1.124) |
 . .
| (1.125) |
Таким образом, мы определили функции  и
и 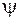 через заданные функции
через заданные функции 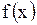 и
и 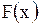 , причем равенства (1.124) и (1.125) имеют место для любого значения
, причем равенства (1.124) и (1.125) имеют место для любого значения  . Заменяя аргумент
. Заменяя аргумент 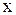 в (1.124) на
в (1.124) на  , а в (1.125) на
, а в (1.125) на  и подставляя найденные функции
и подставляя найденные функции  и
и  в (1.123), получим
в (1.123), получим

и окончательно
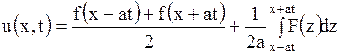 . .
| (1.126) |
Формулу (1.126) называют формулой Даламбера.
|
|
Нетрудно проверить непосредственным дифференцированием, что полученное выражение для 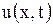 есть решение для волнового уравнения (1.121), удовлетворяющее начальным условиям (1.122). Для этого достаточно предположить, что функция
есть решение для волнового уравнения (1.121), удовлетворяющее начальным условиям (1.122). Для этого достаточно предположить, что функция 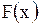 дифференцируема, а функция
дифференцируема, а функция 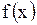 - дважды дифференцируема. Способ вывода формулы (1.126) доказывает как единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении
- дважды дифференцируема. Способ вывода формулы (1.126) доказывает как единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении 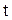 малому изменению функций
малому изменению функций 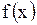 и
и 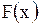 соответствует малое изменение решения.
соответствует малое изменение решения.
РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ХАРАКТЕРИСТИК (МЕТОДОМ ДАЛАМБЕРА)
Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот факт, что с помощью замены 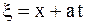 ,
, 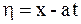 уравнение
уравнение
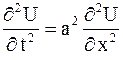
| (2.73) |
преобразуется в уравнение 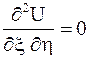 , которое имеет общее решение
, которое имеет общее решение
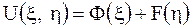 ,
,
где 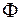 и
и 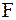 - произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функций
- произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функций 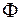 и
и 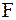 , т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным
, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным 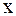 и
и 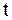 , то общее решение примет вид
, то общее решение примет вид
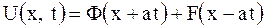 .
.
Здесь 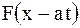 характеризует прямую волну (кривая
характеризует прямую волну (кривая 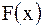 смещается вправо со скоростью
смещается вправо со скоростью 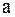 ), а
), а 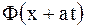 - обратную волну (кривая
- обратную волну (кривая 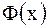 смещается влево со скоростью
смещается влево со скоростью 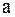 ).
).
Если рассматривается задача Коши для бесконечной струны 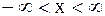 , то по заданным начальным условиям
, то по заданным начальным условиям
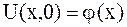 , , 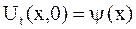
| (2.74) |
определяются функции 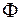 и
и 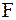 , и искомое решение имеет вид
, и искомое решение имеет вид
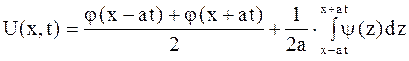 . .
| (2.75) |
Формула (2.75) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши.
В частности, когда начальная скорость равна нулю (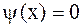 ), то
), то
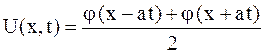 ,
,
откуда легко вычислить отклонение струны от положения равновесия для любой из ее точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 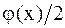 , равной половине начального отклонения.
, равной половине начального отклонения.
|
|
В случае полубесконечной струны, кроме начальных условий (2.74), заданных при 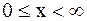 , необходимо добавить еще граничное условие (конец предполагается в точке
, необходимо добавить еще граничное условие (конец предполагается в точке 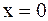 )
)
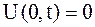
| (2.76) |
для закрепленной в точке 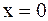 струны,
струны,
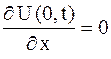
| (2.77) |
для свободного конца в точке 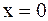 ,
,
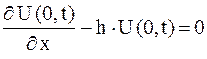 .
.
для упругого закрепления в точке 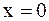 .
.
В случае однородных граничных условий (2.76) или (2.77) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (2.76), т.е. полагают 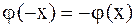 ,
, 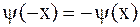 , и четным образом для условия (2.77), т.е.
, и четным образом для условия (2.77), т.е. 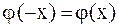 ,
, 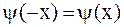 .
.
Примеры решения задач
ПРИМЕР 2.43. Найти форму достаточно длинной струны, определяемой уравнением 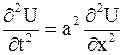 , в момент времени
, в момент времени 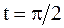 ,
, 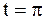 , если заданы начальные смещения и скорости:
, если заданы начальные смещения и скорости:
а) 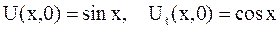 ;
;
б) 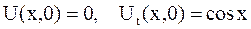 ;
;
в) 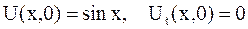 .
.
Решение. По постановке вопроса надо найти решение 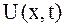 задачи Коши (2.73), (2.74) в области:
задачи Коши (2.73), (2.74) в области: 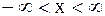 ,
, 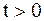 . Оно определяется формулой Даламбера (2.75).
. Оно определяется формулой Даламбера (2.75).
Случай а). Полагая в формуле Даламбера  ,
, 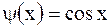 , найдем смещение
, найдем смещение 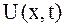 в любой точке и любой момент
в любой точке и любой момент 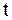 :
:
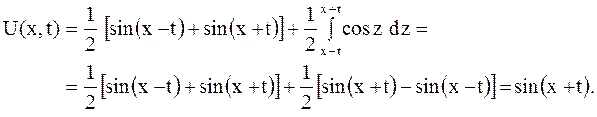
Откуда определяем форму кривой в указанные моменты времени:
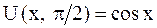 ,
, 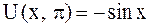 .
.
Кривые изображены на рис. 2.3.
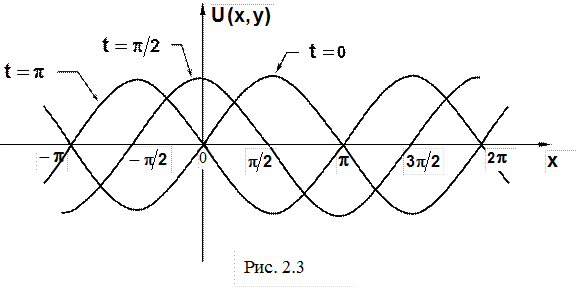
Случай б) Начальные смещения струны равны нулю, т.к. 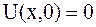 . При
. При 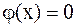 колебательный процесс будет описан по формуле
колебательный процесс будет описан по формуле
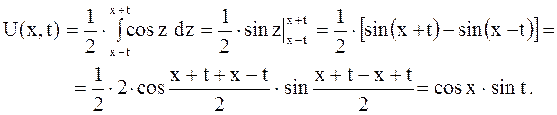
В момент времени 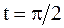 струна имеет форму косинусоиды:
струна имеет форму косинусоиды: 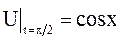 , а в момент
, а в момент 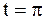 она совпадает с осью абсцисс:
она совпадает с осью абсцисс: 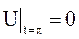 .
.
Случай в). По условию, начальные скорости равны нулю, значит, 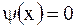 . Тогда имеем
. Тогда имеем
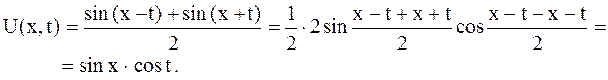
Форма струны в указанные моменты времени определяется уравнениями:
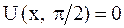 ,
, 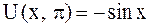 .
.
РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ХАРАКТЕРИСТИК (МЕТОДОМ ДАЛАМБЕРА)
Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот факт, что с помощью замены 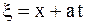 ,
, 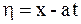 уравнение
уравнение
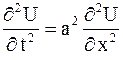
| (2.73) |
преобразуется в уравнение 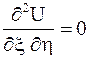 , которое имеет общее решение
, которое имеет общее решение
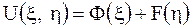 ,
,
где 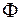 и
и 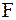 - произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функций
- произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функций 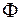 и
и 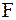 , т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным
, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным 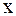 и
и 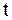 , то общее решение примет вид
, то общее решение примет вид
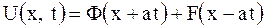 .
.
Здесь 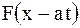 характеризует прямую волну (кривая
характеризует прямую волну (кривая 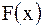 смещается вправо со скоростью
смещается вправо со скоростью 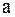 ), а
), а 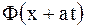 - обратную волну (кривая
- обратную волну (кривая 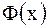 смещается влево со скоростью
смещается влево со скоростью 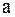 ).
).
Если рассматривается задача Коши для бесконечной струны 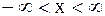 , то по заданным начальным условиям
, то по заданным начальным условиям
|
|
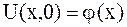 , , 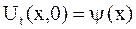
| (2.74) |
определяются функции 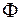 и
и 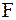 , и искомое решение имеет вид
, и искомое решение имеет вид
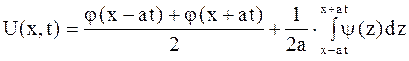 . .
| (2.75) |
Формула (2.75) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши.
В частности, когда начальная скорость равна нулю (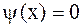 ), то
), то
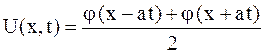 ,
,
откуда легко вычислить отклонение струны от положения равновесия для любой из ее точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 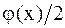 , равной половине начального отклонения.
, равной половине начального отклонения.
В случае полубесконечной струны, кроме начальных условий (2.74), заданных при 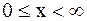 , необходимо добавить еще граничное условие (конец предполагается в точке
, необходимо добавить еще граничное условие (конец предполагается в точке 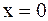 )
)
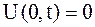
| (2.76) |
для закрепленной в точке 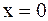 струны,
струны,
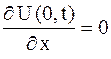
| (2.77) |
для свободного конца в точке 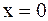 ,
,
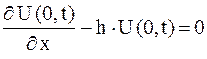 .
.
для упругого закрепления в точке 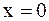 .
.
В случае однородных граничных условий (2.76) или (2.77) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (2.76), т.е. полагают 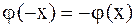 ,
, 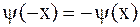 , и четным образом для условия (2.77), т.е.
, и четным образом для условия (2.77), т.е. 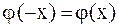 ,
, 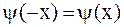 .
.
Примеры решения задач
ПРИМЕР 2.43. Найти форму достаточно длинной струны, определяемой уравнением 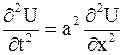 , в момент времени
, в момент времени 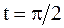 ,
, 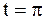 , если заданы начальные смещения и скорости:
, если заданы начальные смещения и скорости:
а) 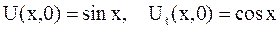 ;
;
б) 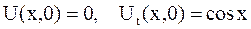 ;
;
в) 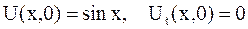 .
.
Решение. По постановке вопроса надо найти решение 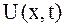 задачи Коши (2.73), (2.74) в области:
задачи Коши (2.73), (2.74) в области: 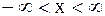 ,
, 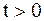 . Оно определяется формулой Даламбера (2.75).
. Оно определяется формулой Даламбера (2.75).
Случай а). Полагая в формуле Даламбера  ,
, 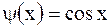 , найдем смещение
, найдем смещение 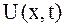 в любой точке и любой момент
в любой точке и любой момент 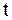 :
:
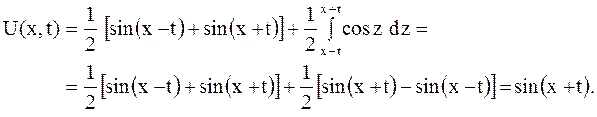
Откуда определяем форму кривой в указанные моменты времени:
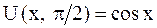 ,
, 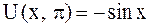 .
.
Кривые изображены на рис. 2.3.

Случай б) Начальные смещения струны равны нулю, т.к. 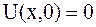 . При
. При 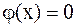 колебательный процесс будет описан по формуле
колебательный процесс будет описан по формуле
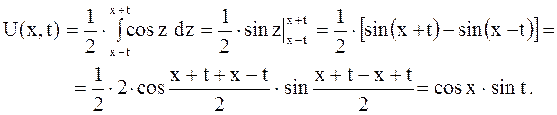
В момент времени 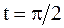 струна имеет форму косинусоиды:
струна имеет форму косинусоиды: 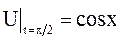 , а в момент
, а в момент 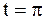 она совпадает с осью абсцисс:
она совпадает с осью абсцисс: 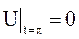 .
.
Случай в). По условию, начальные скорости равны нулю, значит, 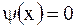 . Тогда имеем
. Тогда имеем
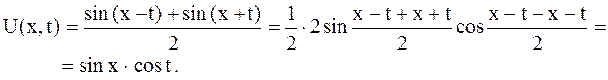
Форма струны в указанные моменты времени определяется уравнениями:
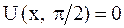 ,
, 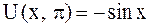 .
.
Колебания однородной бесконечной струны.
Формула Даламбера
Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с более простой задачи – задачи о свободных колебаниях однородной бесконечной струны. Это задача, как было показано в п. 1.24, сводится к решению уравнения
|
|

| (1.121) |
при начальных условиях
 , ,  , ,
| (1.122) |
где функции 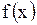 и
и 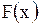 заданы на всей числовой оси. Никакие граничные условия на искомую функцию
заданы на всей числовой оси. Никакие граничные условия на искомую функцию 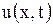 не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши.
не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши.
Для решения поставленной задачи преобразуем уравнение (1.121) к каноническому виду, содержащему смешанную производную (см. (1.93)). Для чего составим уравнение характеристик
 ,
,
которое распадается на два уравнения:
 и
и  .
.
Интегрируя эти уравнения, получим
 и
и  .
.
Согласно общей теории о замене переменных полагаем
 ,
,  .
.
Тогда уравнение (1.121) преобразуется к виду
 .
.
Как было показано в п.1.18 (см. формулу (1.87)), общее решение такого уравнения имеет вид
 ,
,
где  и
и  - произвольные функции. Возвращаясь к старым переменным
- произвольные функции. Возвращаясь к старым переменным 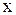 и
и 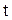 , получим общее решение волнового уравнения (1.121)
, получим общее решение волнового уравнения (1.121)
 . .
| (1.123) |
Определим функции  и
и 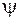 таким образом, чтобы удовлетворялись начальные условия (1.122)
таким образом, чтобы удовлетворялись начальные условия (1.122)
 ,
,
 .
.
Интегрируя последнее равенство по  , получим
, получим
 , где
, где 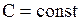 .
.
Из равенств
 ,
,

находим
 , ,
| (1.124) |
 . .
| (1.125) |
Таким образом, мы определили функции  и
и 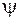 через заданные функции
через заданные функции 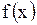 и
и 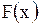 , причем равенства (1.124) и (1.125) имеют место для любого значения
, причем равенства (1.124) и (1.125) имеют место для любого значения  . Заменяя аргумент
. Заменяя аргумент 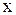 в (1.124) на
в (1.124) на  , а в (1.125) на
, а в (1.125) на  и подставляя найденные функции
и подставляя найденные функции  и
и  в (1.123), получим
в (1.123), получим

и окончательно
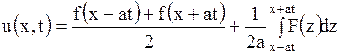 . .
| (1.126) |
Формулу (1.126) называют формулой Даламбера.
Нетрудно проверить непосредственным дифференцированием, что полученное выражение для 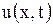 есть решение для волнового уравнения (1.121), удовлетворяющее начальным условиям (1.122). Для этого достаточно предположить, что функция
есть решение для волнового уравнения (1.121), удовлетворяющее начальным условиям (1.122). Для этого достаточно предположить, что функция 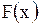 дифференцируема, а функция
дифференцируема, а функция 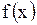 - дважды дифференцируема. Способ вывода формулы (1.126) доказывает как единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении
- дважды дифференцируема. Способ вывода формулы (1.126) доказывает как единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении 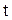 малому изменению функций
малому изменению функций 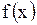 и
и 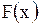 соответствует малое изменение решения.
соответствует малое изменение решения.
|
|
|

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!