
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Лекция 7. Определенный интеграл
Пусть  – непрерывная на
– непрерывная на  функция и и
функция и и  – ее первообразная (любая)*. Тогда разность значений первообразной
– ее первообразная (любая)*. Тогда разность значений первообразной  в точках b и a:
в точках b и a:

называется определенным интегралом функции  на отрезке
на отрезке  . Определенный интеграл обозначается так:
. Определенный интеграл обозначается так:
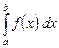 .
.
В соответствии с определением
 . (1)
. (1)
Эта формула называется формулой Ньютона-Лейбница. Применяют также обозначается:
 . (2)
. (2)
Примеры:
1)  ;
;
2)  ;
;
3) 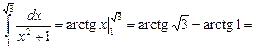
 .
.
Свойства определенных интегралов
1. Постоянный множитель можно выносить за знак интеграла
 . (3)
. (3)
2. Определенный интеграл от алгебраической суммы равен алгебраической сумме определенных интегралов:
 . (4)
. (4)
Пример. Вычислить  .
.
На основании свойств 1 и 2 получаем


3. Определенный интеграл меняет знак при перестановке пределов интегрирования
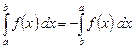 . (5)
. (5)
Это следует из того, что
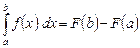 , а
, а 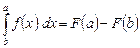 .
.
4. Теорема о среднем. Между точками a и b имеется такая точка c, что
 . (6)
. (6)
Доказательство. По формуле Ньютона-Лейбница 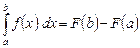 . Применим к первообразной
. Применим к первообразной  формулу Лагранжа:
формулу Лагранжа:  . Но
. Но 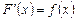 , следовательно
, следовательно  . Итак,
. Итак,
 .
.
5. Если  и
и  , то
, то
 . (7)
. (7)
Действительно, в этом случае  и
и  , и из формулы (6) получаем
, и из формулы (6) получаем
 .
.
6. Если  и
и  , то
, то
 . (8)
. (8)
Действительно,
 .
.
По условию  и по свойству 5:
и по свойству 5:
 .
.
Следовательно,
 .
.
7. Если  , то
, то
 . (9)
. (9)
Это следует из того, что  .
.
Приложения определенного интеграла
Рассмотрим приложения интеграла к вычислению площадей, объемов, механической работы.
Вычисление площадей
Пусть  – непрерывная на
– непрерывная на  функция,
функция,  . Рассмотрим фигуру, ограниченную сверху графиком функции
. Рассмотрим фигуру, ограниченную сверху графиком функции  , снизу – отрезком
, снизу – отрезком  оси Ox, с боков – прямыми
оси Ox, с боков – прямыми  ,
,  .
.

|
| Рис. 1 |
Эту фигуру называют криволинейной трапецией. Площадь S этой фигуры вычисляется по формуле
|
|
 . (1)
. (1)
Приведем обоснование этой формулы. Для того чтобы определить площадь криволинейной трапеции ABCD (см. рис. 2), изучим поведение площади переменной фигуры ABMN, заключенной между начальной ординатой  и ординатой, соответствующей произвольно выбранному на
и ординатой, соответствующей произвольно выбранному на  значению x. Площадь этой криволинейной трапеции ABMN есть функция, зависящая от x; обозначим ее через
значению x. Площадь этой криволинейной трапеции ABMN есть функция, зависящая от x; обозначим ее через  .
.

|
| Рис. 2 |
Вычислим производную этой функции  . Для этого придадим x приращение D x. Тогда площадь
. Для этого придадим x приращение D x. Тогда площадь  получит приращение D S, равное площади фигуры
получит приращение D S, равное площади фигуры  . Если приращение D x мало, то D S приблизительно равно площади прямоугольника
. Если приращение D x мало, то D S приблизительно равно площади прямоугольника  , равной
, равной  . Рассмотрим отношение
. Рассмотрим отношение 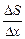 . Оно приблизительно равно
. Оно приблизительно равно  . Если
. Если  , то приближенное равенство перейдет в точное
, то приближенное равенство перейдет в точное
 .
.
Итак, переменная площадь  есть первообразная для
есть первообразная для  . Следовательно, если
. Следовательно, если  – какая-нибудь первообразная для
– какая-нибудь первообразная для  , то
, то
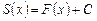 .
.
Положим  . Очевидно,
. Очевидно,  . Следовательно,
. Следовательно,
 .
.
Поэтому
 .
.
При  получаем
получаем
 .
.
Но это означает, что
 .
.
Пример 1. Найти площадь фигуры (криволинейной трапеции), ограниченной параболой  , прямыми
, прямыми  ,
,  и осью Ox.
и осью Ox.
Решение.
 .
.
Пример 2. Найти площадь фигуры, ограниченной линиями  ,
,  .
.

| Решение. Очевидно, эти линии пересекаются в точках с абсциссами  и и  . Искомая площадь есть разность площадей криволинейных трапеций, ограниченных сверху соответственно линиями . Искомая площадь есть разность площадей криволинейных трапеций, ограниченных сверху соответственно линиями  и и  : :
|
 .
.
В примере 2 рассмотрен частный случай вычисления площади фигуры, ограниченной одной кривой сверху, другой кривой – снизу.
Вообще, если фигура ограничена сверху кривой  , снизу – кривой
, снизу – кривой  , а с боков – соответственно прямыми
, а с боков – соответственно прямыми  ,
,  , то ее площадь выражается формулой:
, то ее площадь выражается формулой:
 . (2)
. (2)
Лекция 9. Ряды
Числовые ряды
Определение 1. Числовым рядом называется бесконечная последовательность чисел  ,
,  ,...,
,...,  ,..., соединенных знаком сложения:
,..., соединенных знаком сложения:
 . (1)
. (1)
Числа  ,
,  ,...,
,...,  ,..., называются членами ряда, а n -й член
,..., называются членами ряда, а n -й член  – общим членом ряда.
– общим членом ряда.
Ряд считается заданным, если известен его общий член  . Например, ряд с общим членом
. Например, ряд с общим членом  имеет вид
имеет вид
|
|
 ,
,
или
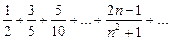 .
.
Иначе его можно записать в виде  .
.
Рассмотрим суммы первых членов ряда (1):



............

............
Эти суммы называются частичными суммами ряда (1). Сумма  называется n -й частичной суммой ряда (1).
называется n -й частичной суммой ряда (1).
Определение 2. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.
 . (2)
. (2)
Этот предел S называется суммой ряда.
Если предел (2) не существует, то ряд называется расходящимся.
Пример. Рассмотрим ряд
 . (3)
. (3)
Это – геометрическая прогрессия (точнее говоря, ряд, составленный из членов геометрической прогрессии).
Из школьного курса известно, что сумма n членов геометрической прогрессии равна

или
 .
.
Это и есть n -я частичная сумма ряда (3).
Пусть  . Тогда
. Тогда  , следовательно,
, следовательно,
 .
.
Итак, в случае  ряд (3) сходится и его сумма
ряд (3) сходится и его сумма
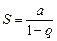
Нетрудно убедиться в том, что при  ряд (3) расходится.
ряд (3) расходится.
Свойства сходящихся рядов
1. Если ряд  сходится и имеет сумму S, то ряд
сходится и имеет сумму S, то ряд  (полученный почленным умножением данного ряда на число k) также сходится и имеет сумму kS.
(полученный почленным умножением данного ряда на число k) также сходится и имеет сумму kS.
2. Если ряды  и
и  сходятся и их суммы соответственно равны
сходятся и их суммы соответственно равны  и
и  , то и ряд
, то и ряд  также сходится и его сумма равна
также сходится и его сумма равна  .
.
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
Если в ряде (1) отбросить первые n членов, то получится ряд
 , (4)
, (4)
называемый n -м остатком ряда.
Очевидно, если ряд (1) сходится, то и его остаток (4) также сходится. Если сумму остатка (4) обозначить через  , т.е.
, т.е.
 ,
,
то сумму ряда (1) можно представить в виде
 . (5)
. (5)
Отсюда получаем свойство 4.
4. Для того чтобы ряд (1) сходился, необходимо и достаточно, чтобы при  остаток ряда стремился к нулю, т.е.
остаток ряда стремился к нулю, т.е.  .
.
Знакочередующиеся ряды
Рассмотрим ряд
 ,
,
где  при всех n.
при всех n.
Такой ряд называется знакочередующимся.
Признак Лейбница. Если члены знакочередующегося ряда убывают по абсолютной величине:
 ,
,
и предел общего члена этого ряда при  равен нулю, то ряд сходится, а его сумма не превосходит первого члена:
равен нулю, то ряд сходится, а его сумма не превосходит первого члена:  .
.
Пример. Исследовать ряд

Решение. Члены ряда убывают по абсолютной величине:  и предел общего члена равен нулю:
и предел общего члена равен нулю:  . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
Рассмотренные нами знакочередующиеся ряды представляют собой частный случай знакопеременных рядов. Ряд
 (*)
(*)
называется знакопеременным, если любой его член  может быть как положительным, так и отрицательным.
может быть как положительным, так и отрицательным.
|
|
Различают абсолютную и условную сходимость знакопеременного ряда.
Ряд (*) называется абсолютно сходящимся, если ряд, составленный из модулей его членов, т.е. ряд
 , (**)
, (**)
сходится.
Можно доказать, что абсолютно сходящийся ряд сходится в обычном смысле.
Ряд (*) называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, т.е. ряд (**), расходится.
Очевидно, ряд, рассмотренный в последнем примере, сходится условно.
Лекция 7. Определенный интеграл
Пусть  – непрерывная на
– непрерывная на  функция и и
функция и и  – ее первообразная (любая)*. Тогда разность значений первообразной
– ее первообразная (любая)*. Тогда разность значений первообразной  в точках b и a:
в точках b и a:

называется определенным интегралом функции  на отрезке
на отрезке  . Определенный интеграл обозначается так:
. Определенный интеграл обозначается так:
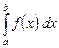 .
.
В соответствии с определением
 . (1)
. (1)
Эта формула называется формулой Ньютона-Лейбница. Применяют также обозначается:
 . (2)
. (2)
Примеры:
1)  ;
;
2)  ;
;
3) 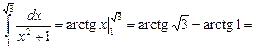
 .
.
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
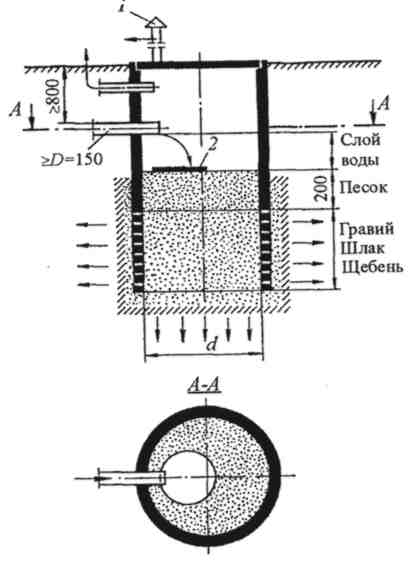
Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!