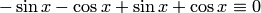Двойным интегралом называют кратный интеграл с  .
.
 . Здесь
. Здесь  — элемент площади в рассматриваемых координатах.
— элемент площади в рассматриваемых координатах.
В прямоугольных координатах:  , где
, где  — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах.
Геометрический смысл двойного интеграла
Пусть функция  принимает в области
принимает в области  только положительные значения. Тогда двойной интеграл
только положительные значения. Тогда двойной интеграл  численно равен объему
численно равен объему  вертикального цилиндрического тела, построенного на основании
вертикального цилиндрического тела, построенного на основании  и ограниченного сверху соответствующим куском поверхности
и ограниченного сверху соответствующим куском поверхности  .
.
Физический смысл
Если рассматривать перемещение, то первая производная - скорость, вторая - ускорение.
Соответственно, интеграл от ускорения - это скорость, двойной интеграл - перемещение.
Если рассмотреть график ускорения, то двойной интеграл от него - площадь под графиком.
Область D называется правильной в направлении оси OY (ОХ), если любая прямая, параллельная оси OY(OX) и проходящая через внутреннюю точку области Д пересекает ее границу в двух точках.

Рис. 23.3

Рис. 23.4
Граница области D, правильной в направлении оси OY (рис. 23.3), может быть задана уравнениями 
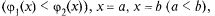 и двойной интеграл в этом случае вычисляется по формуле
и двойной интеграл в этом случае вычисляется по формуле
 (23.5)
(23.5)
причем сначала вычисляется внутренний интеграл 
в котором х считается постоянной. Выражение справа в (23.5) называется повторным, или двукратным интегралом.
Граница области D, правильной в направлении оси ОХ (рис. 23.4), может быть задана уравнениями: 
 Тогда двойной интеграл вычисляется по формуле
Тогда двойной интеграл вычисляется по формуле
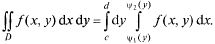 (23.6)
(23.6)
Если область D правильная в направлении ОХ и OY (правильная область), то применимы обе формулы.
Рассмотрим геометрический смысл формулы (23.5), для формулы (23.6) рассуждения аналогичные (вывод формул приведен в [6. С. 310]).
Предположим, что  и граница области D является правильной в направлении оси OY.
и граница области D является правильной в направлении оси OY.
Из разд. 23.1 
Подсчитаем теперь объем V методом поперечных сечений (см. п.18.2.1):
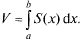 (23.7)
(23.7)
Проводя через т. (х,0,0) плоскость перпендикулярно оси ОХ, получим в сечении криволинейную трапецию 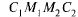
(рис. 23.5), с площадью 
для точек линии  при постоянном х зависит только от у:
при постоянном х зависит только от у:
 - (23.8)
- (23.8)
площадь поперечного сечения цилиндрического тела. Подставляя (23.8) в (23.7), получаем


Рис. 23.5
Таким образом, в формуле (23.7) слева и справа имеем объем цилиндрического тела.
Формулы (23.5) и (23.6) выведены в предположении, что область имеет специальный вид.
В общем случае область D разбивают на конечное число частей, являющихся правильными, и вычисляют для каждой из частей интеграл по формуле (23.5) или (23.6). Интеграл по всей области (свойство 3°) равен сумме полученных интегралов.
Если область ГУ.  то формулы (23.5) и (23.6)
то формулы (23.5) и (23.6)
примут вид

Пример: 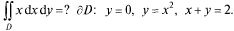
Решение разбивается на три этапа:
1) построение области D;
2) переход к повторному интегралу, расстановка пределов интегрирован ия;
3) вычисление повторного интеграла.
Решая систему  находим т. пересечения параболы
находим т. пересечения параболы
и прямой (1, 1), (-2, 4). Строим область, (-2, 4)  D (рис. 23.6). Так как область правильная, то можно воспользоваться формулами (23.5) и (23.6).
D (рис. 23.6). Так как область правильная, то можно воспользоваться формулами (23.5) и (23.6).
При решении по (23.5) область придется разбить на две: ОВС и СВА, так как линия ОБА задается разными уравнениями:
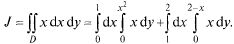

Рис. 23.6
При вычислении по формуле (23.6) приходим к одному повторному интегралу  Закончим решение, пользуясь последней формулой:
Закончим решение, пользуясь последней формулой:

Дифференциал уравнения. Основные понятия. Нахождение уравнения по его решению
Дифференциальным уравнением называется уравнение, связывающее независимую переменную  , искомую функцию
, искомую функцию 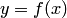 и её производные
и её производные 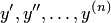 , т. е. уравнение вида
, т. е. уравнение вида

Если искомая функция 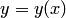 есть функция одной независимой переменной
есть функция одной независимой переменной  , дифференциальное уравнение называется обыкновенным.
, дифференциальное уравнение называется обыкновенным.
Когда искомая функция  есть функция двух и более независимых переменных, например, если
есть функция двух и более независимых переменных, например, если 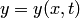 , то уравнение вида
, то уравнение вида
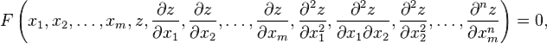
называется уравнением в частных производных. Здесь  — неотрицательные целые числа, такие, что
— неотрицательные целые числа, такие, что 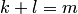 .
.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение 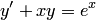 — уравнение первого порядка, дифференциальное уравнение
— уравнение первого порядка, дифференциальное уравнение  , где
, где 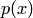 — известная функция, — уравнение второго порядка; дифференциальное уравнение
— известная функция, — уравнение второго порядка; дифференциальное уравнение 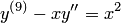 — уравнение 9-го порядка.
— уравнение 9-го порядка.
Решением дифференциального уравнения n-го порядка на интервале 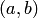 называется функция
называется функция 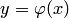 , определенная на интервале
, определенная на интервале 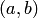 вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции
вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции 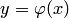 в дифференциальное уравнение превращает последнее в тождество по
в дифференциальное уравнение превращает последнее в тождество по  на
на 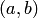 . Например, функция
. Например, функция 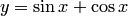 является решением уравнения
является решением уравнения  на интервале
на интервале 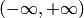 . В самом деле, дифференцируя функцию дважды, будем иметь
. В самом деле, дифференцируя функцию дважды, будем иметь
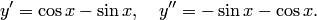
Подставляя выражения 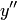 и
и  в дифференциальное уравнение, получим тождество
в дифференциальное уравнение, получим тождество
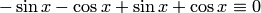
График решения дифференциального уравнения называется интегральной кривой этого уравнения.



 .
. . Здесь
. Здесь  — элемент площади в рассматриваемых координатах.
— элемент площади в рассматриваемых координатах. , где
, где  — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах. принимает в области
принимает в области  только положительные значения. Тогда двойной интеграл
только положительные значения. Тогда двойной интеграл  численно равен объему
численно равен объему  вертикального цилиндрического тела, построенного на основании
вертикального цилиндрического тела, построенного на основании  .
.


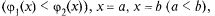 и двойной интеграл в этом случае вычисляется по формуле
и двойной интеграл в этом случае вычисляется по формуле (23.5)
(23.5)

 Тогда двойной интеграл вычисляется по формуле
Тогда двойной интеграл вычисляется по формуле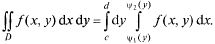 (23.6)
(23.6) и граница области D является правильной в направлении оси OY.
и граница области D является правильной в направлении оси OY.
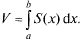 (23.7)
(23.7)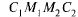

 при постоянном х зависит только от у:
при постоянном х зависит только от у: - (23.8)
- (23.8)

 то формулы (23.5) и (23.6)
то формулы (23.5) и (23.6)
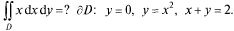
 находим т. пересечения параболы
находим т. пересечения параболы D (рис. 23.6). Так как область правильная, то можно воспользоваться формулами (23.5) и (23.6).
D (рис. 23.6). Так как область правильная, то можно воспользоваться формулами (23.5) и (23.6).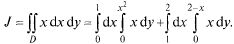

 Закончим решение, пользуясь последней формулой:
Закончим решение, пользуясь последней формулой:
 , искомую функцию
, искомую функцию 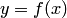 и её производные
и её производные 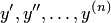 , т. е. уравнение вида
, т. е. уравнение вида
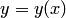 есть функция одной независимой переменной
есть функция одной независимой переменной  есть функция двух и более независимых переменных, например, если
есть функция двух и более независимых переменных, например, если 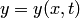 , то уравнение вида
, то уравнение вида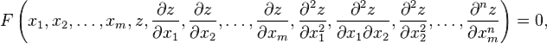
 — неотрицательные целые числа, такие, что
— неотрицательные целые числа, такие, что 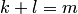 .
.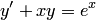 — уравнение первого порядка, дифференциальное уравнение
— уравнение первого порядка, дифференциальное уравнение  , где
, где 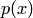 — известная функция, — уравнение второго порядка; дифференциальное уравнение
— известная функция, — уравнение второго порядка; дифференциальное уравнение 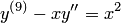 — уравнение 9-го порядка.
— уравнение 9-го порядка.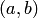 называется функция
называется функция 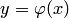 , определенная на интервале
, определенная на интервале 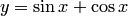 является решением уравнения
является решением уравнения  на интервале
на интервале 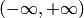 . В самом деле, дифференцируя функцию дважды, будем иметь
. В самом деле, дифференцируя функцию дважды, будем иметь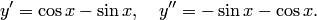
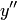 и
и