Для того чтобы можно было всесторонне проанализировать исследуемый признак, необходимо вычислить целый ряд статистических показателей, характеризующих объект исследования. Основные из них - следующие.
2.1 Средние величины. Среднее арифметическое значение .
Этот показатель вычисляется по формуле
 ,
,
где к — количество классов; xi— значение i-гo класса (середина интервала, если ряд интервальный);  —частота i-го класса. Средняя арифметическая величина, вычисленная по формуле, называется - взвешенной.
—частота i-го класса. Средняя арифметическая величина, вычисленная по формуле, называется - взвешенной.
Средняя арифметическая величина используется для оценки математического ожидания исследуемой случайной величины.
В том случае, если исходные данные сгруппированы в статистический ряд, среднее квадратическое значение можно вычислить следующим образом:

Среднее квадратическое значение используется лесоводами в качестве таксационного среднего диаметра древостоя. Это вызвано тем, что, согласно определяющему свойству, при замене всех элементов выборки на среднее квадратическое остается постоянной сумма квадратов элементов выборки. А эта величина позволяет вычислить сумму площадей сечений древостоя, являющуюся важнейшим таксационным показателем:

где G - сумма площадей сечения древостоя;  — площадь сечения i-го дерева; dt —диаметр i-го дерева,
— площадь сечения i-го дерева; dt —диаметр i-го дерева, 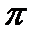 = 3,14;
= 3,14;  - среднеквадратический диаметр древостоя.
- среднеквадратический диаметр древостоя.
Рассмотрим порядок вычисления средних величин на примере вариационных рядов по диаметрам и высотам. Для выполнения вычислений составим вспомогательную таблицу.
Таблица 5 ─ Вычисление средних значений (диаметры)
| Xi
| fi
| Xifi
| Xi2
| Xi2fi
| gi
| gi fi
|
| 15,6
|
| 46,8
| 730,08
| 0,0191
| 0,0573
| 15,6
|
| 18,5
|
| 129,5
| 2395,75
| 0,0268
| 0,1876
| 18,5
|
| 21,4
|
| 385,2
| 8243,28
| 0,0359
| 0,6462
| 21,4
|
| 24,3
|
| 656,1
| 15943,23
| 0,0463
| 1,2501
| 24,3
|
| 27,2
|
| 870,4
| 23674,88
| 0,0580
| 1,856
| 27,2
|
| 30,1
|
| 933,1
| 28086,31
| 0,0711
| 2,2041
| 30,1
|
|
|
|
|
| 0,0854
| 1,6226
|
|
| 35,9
|
| 861,6
| 30931,44
| 0,1011
| 2,4264
| 35,9
|
| 38,8
|
| 698,4
| 27097,92
| 0,1181
| 2,1258
| 38,8
|
| 41,7
|
| 250,2
| 10433,34
| 0,1365
| 0,819
| 41,7
|
| 44,6
|
| 178,4
| 7956,64
| 0,1561
| 0,6244
| 44,6
|
| 47,5
|
| 332,5
| 15793,75
| 0,1771
| 1,2397
| 47,5
|
| 50,4
|
| 201,6
| 10160,64
| 0,1994
| 0,7976
| 50,4
|
| Сумма
|
| 6170,8
| 202138,26
|
| 15,8568
| Сумма
|
Теперь, пользуясь формулами, вычислим среднее арифметическое значение:
 см
см
и среднее квадратическое:
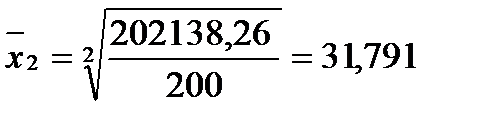 см
см
Теперь на основе полученной средней квадратической вычислим сумму площадей сечений древостоя. Для этого определим площадь сечения, соответствующую среднеквадратическому диаметру:

Умножив полученную величину на число стволов, получим сумму площадей сечений древостоя:
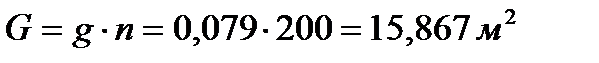
Сравнивая полученную величину с площадью сечения, вычисленной по данным ряда диаметров, видим, что среднее квадратическое значение позволяет очень точно определять важнейший таксационный показатель — сумму площадей сечений древостоя.
Аналогичным образом определим средние значения для ряда высот. Сначала составим вспомогательную таблицу.
Таблица 6 ─ Вычисление средних значений (высоты)
| Xi
| fi
| Xifi
| Xi2fi
|
| 17,7
|
| 70,8
| 1253,16
|
| 18,6
|
| 55,8
| 1037,88
|
| 19,5
|
|
|
|
| 20,4
|
|
| 2080,8
|
| 21,3
|
| 149,1
| 3175,83
|
| 22,2
|
| 355,2
| 7885,44
|
| 23,1
|
| 438,9
| 8339,1
|
|
|
|
|
|
| 24,9
|
| 647,4
| 16120,26
|
| 25,8
|
|
| 29953,8
|
| 26,7
|
| 667,5
| 17822,25
|
| 27,6
|
| 331,2
| 9141,12
|
| 28,5
|
|
| 1624,5
|
| 29,4
|
| 58,8
| 1728,72
|
| Сумма
|
| 4892,7
| 118963,86
|
Далее, подставляя полученные суммы в формулы, вычисляем среднее арифметическое значение:
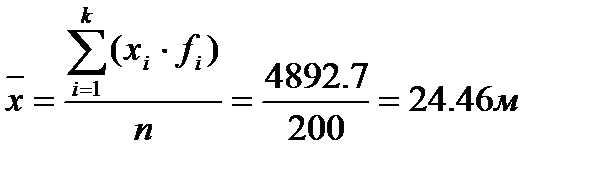
и среднее квадратическое:

Показатели вариации
Средние величины указывают на то значение признака, вокруг которого группируются анализируемые наблюдения. Однако вокруг одного и того же значения признака наблюдения могут располагаться совершенно по-разному. Для того чтобы отразить характер расположения наблюдений вокруг среднего, и служат показатели вариации. Рассмотрим некоторые из них.
Размах вариации. Это наиболее простой показатель, характеризующий распределение вариант вокруг среднего. Он вычисляется как разность между максимальным и минимальным значениями признака, которые в биометрии называют также лимитами(от латинского слова limes - предел) и обозначают символом lim:
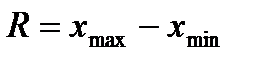
Если наблюдения плотно группируются вокруг среднего, то лимиты располагаются близко друг к другу и размах вариации оказывается небольшим. Если же разброс данных велик, то, как правило, минимальная и максимальная варианты располагаются далеко друг от друга и размах вариации получается большим.
Однако размах вариации является ненадежным показателем, так как он вычисляется на основании значений лимитов, а последние, в свою очередь, являются очень неустойчивыми статистиками и могут значительно варьировать от выборки к выборке. Кроме того, так как при вычислении размаха вариации используются только две крайние варианты, то он не дает нам никакой информации о характере распределения всех остальных вариант, располагающихся ближе к среднему.
Эмпирическая дисперсия.Этот показатель получил свое название от латинского слова dispersio - рассеяние. Это не что иное, как средний квадрат отклонений вариант от среднего арифметического. Вычисляется дисперсия так:

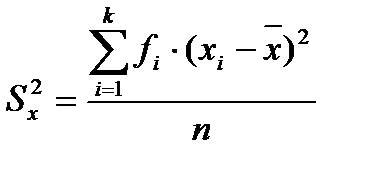 ,
,
Выборочная дисперсия, рассчитанная по формуле, дает смещенную оценку генеральной дисперсии. Для того чтобы получить несмещенную оценку, в формулу необходимо добавить сомножитель 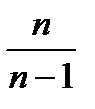 , называемый поправкой Бесселя:
, называемый поправкой Бесселя:
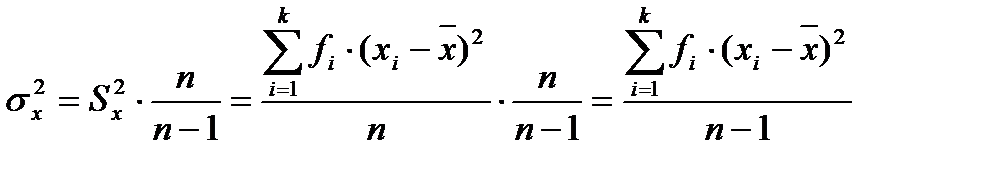 ,
,
Величина n —1 из формулы называется числом степеней свободы. Она показывает, сколько в данном случае имеется независимых наблюдений.
Среднеквадратическое отклонение.Дисперсия часто применяется для оценки вариации данных, однако иногда для характеристики изменчивости признака удобнее использовать среднеквадратическое отклонение, которое
является квадратным корнем из дисперсии:
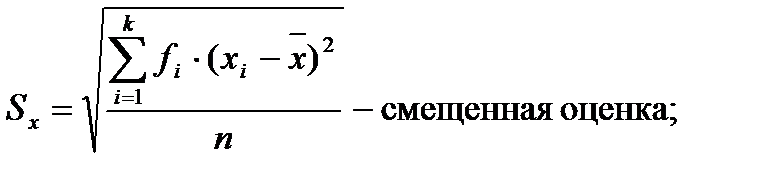
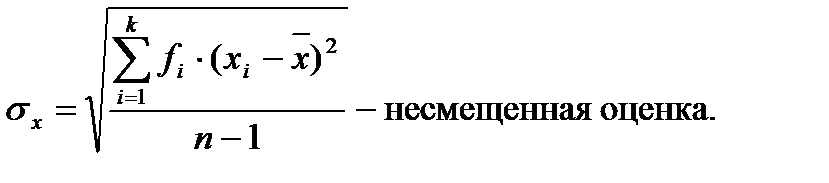
В отличие от дисперсии, среднеквадратическое отклонение выражается в тех же единицах измерения, что и анализируемый признак. В связи с этим данный показатель является более естественным и легче поддается анализу.
Коэффициент вариации. Дисперсия и среднеквадратическое отклонение довольно полно характеризуют вариацию, однако часто удобнее иметь показатель, оценивающий разброс данных не в абсолютных величинах, а в относительных. Таким показателем является коэффициент вариации. Он показывает, сколько процентов составляет среднеквадратическое отклонение от среднего арифметического:
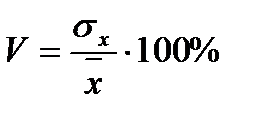
В биометрии этот показатель часто оказывается весьма полезным. Дело в том, что анализу подвергаются, как правило, объекты живой природы, а они с течением времени изменяют свои размеры, растут. В связи с этим часто необходимо анализировать выборки, сделанные для объектов с разным средним возрастом, а следовательно, и с разными средними размерами. Если в таких случаях необходимо сравнить степень изменчивости признака в разных выборках, то удобнее оперировать коэффициентом вариации, так как он даст нам величину вариации по отношению к среднему значению.
Коэффициент асимметрии. Рассмотренные выше показатели довольно полно характеризуют анализируемые признаки, однако ни один из них не отражает степень симметричности распределения наблюдений относительно среднего значения.
Для того чтобы оценить степень такой неравномерности распределения наблюдений относительно среднего арифметического, используют коэффициент асимметрии, который можно вычислить по формуле:
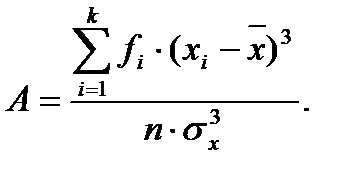
Коэффициент асимметрии может принимать как положительные, так и отрицательные значения. В том случае, если левая ветвь распределения более пологая и длинная, а вершина кривой смещена вправо относительно среднего арифметического, то коэффициент асимметрии для такого распределения имеет отрицательное значение. Такая асимметрия называется левосторонней или отрицательной.
Если распределение имеет более длинную и пологую правую ветвь, а его вершина смещена влево относительно среднего арифметического, то в таком случае имеет место правосторонняя, или положительная, асимметрия. Коэффициент асимметрии в таком случае будет положительным.
Эмпирический коэффициент эксцесса. Кроме того, что распределения наблюдений могут отличаться друг от друга по степени асимметричности, они могут иметь разную крутизну. Распределения могут быть островершинными и плосковершинными. В случае островершинной кривой, когда большое число наблюдений группируется в непосредственной близости от центра распределения, говорят о наличии положительного эксцесса. Кривая распределения имеет отрицательный эксцесс, если она является плосковершинной. Для оценки степени крутизны кривой распределения используется коэффициент эксцесса, который вычисляется по формуле:
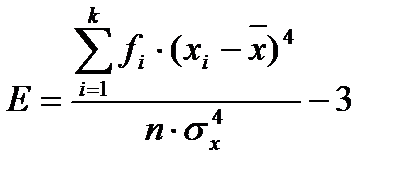
Этот коэффициент построен таким образом, что его значение для нормального распределения, как для наиболее изученного и часто используемого, равен нулю. В том случае, если коэффициент эксцесса принимает положительное значение (положительный эксцесс), распределение вариант будет более крутым, чем нормальное распределение. Когда этот показатель меньше нуля (отрицательный эксцесс), наблюдения будут образовывать более плосковершинную кривую, чем нормальное распределение.
Эмпирические моменты.Кроме рассмотренных выше показателей, для характеристики массовых данных используется система статистик, называемых моментами. Если с - константа, то выражением:
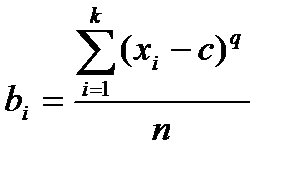 ,
,
задается момент относительно точки с порядка q.
Моменты, вычисленные относительно средней арифметической 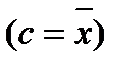 , называются центральными:
, называются центральными:
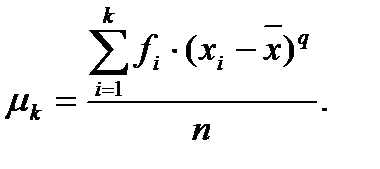
Для того чтобы определить остальные показатели вариации, составим по данным вариационных рядов диаметров и высот вспомогательные таблицы.
Таблица 7 ─ Вычисление показателей вариации (диаметры)
| Xi
| fi
| xi − x.
| (xi − x)2
| (xi − x)3 ⋅ fi
| (xi − x)4 ⋅ fi
|
| 15,6
|
| -15,524
| 722,98
| -11223,54
| 174234,24
|
| 18,5
|
| -12,354
| 1068,34
| -13198,27
| 163051,43
|
| 21,4
|
| -9,454
| 1608,80
| -15209,59
| 143791,46
|
| 24,3
|
| -6,55
| 1158,37
| -7587,32
| 49696,95
|
| 27,2
|
| -3,65
| 426,32
| -1556,07
| 5679,66
|
| 30,1
|
| -0,75
| 17,44
| -13,08
| 9,81
|
|
|
| 2,15
| 87,83
| 188,83
| 405,98
|
| 35,9
|
| 5,05
| 612,06
| 3090,90
| 15609.05
|
| 38,8
|
| 7,95
| 1137,64
| 9044,23
| 71901,63
|
| 41,7
|
| 10,85
| 706,335
| 7663,73
| 83151,47
|
| 44,6
|
| 13,75
| 756,25
| 10398,44
| 142978,55
|
| 47,5
|
| 16,65
| 1940,55
| 32310,16
| 537964,164
|
| 50,4
|
| 19,55
| 1528,81
| 29888,24
| 584315,09
|
| Сумма
|
| 27,938
| 11771,73
| 43796,66
| 1972789,48
|
Таблица 8 ─ Вычисление показателей вариации (высоты)
| Xi
| fi
| xi − x.
| (xi − x)2
| (xi − x)3 ⋅ fi
| (xi − x)4 ⋅ fi
|
| 17,7
|
| -6,76
| 182,79
| -1235,66
| 8353,06
|
| 18,6
|
| -5,86
| 103,01
| -603,69
| 3537,62
|
| 19,5
|
| -4,96
| 98,41
| -488,09
| 2420,95
|
| 20,4
|
| -4,06
| 82,42
| -334,61
| 1358,64
|
| 21,3
|
| -3,16
| 69,90
| -220,88
| 697,98
|
| 22,2
|
| -2,26
| 81,72
| -184,69
| 417,40
|
| 23,1
|
| -1,36
| 35,14
| -47,79
| 64,99
|
|
|
| -0,46
| 6,35
| -2,92
| 1,34
|
| 24,9
|
| 0,43
| 4,81
| 2,06
| 0,88
|
| 25,8
|
| 1,33
| 79,60
| 105,86
| 140,81
|
| 26,7
|
| 2,23
| 124,32
| 277,24
| 618,24
|
| 27,6
|
| 3,13
| 117,56
| 367,97
| 1151,75
|
| 28,5
|
| 4,03
| 32,48
| 130,90
| 527,52
|
| 29,4
|
| 4,93
| 49,20
| 242,57
| 1195,87
|
| Сумма
|
| -9,16
| 1067,71
| -880,75
| 20487,05
|
Подставляя значения из этих таблиц в формулы, получим оценки остальных показателей вариации для диаметров и высот:
Диаметры:
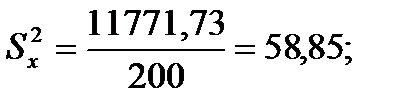
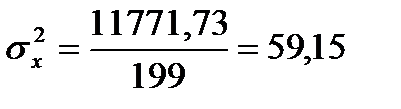
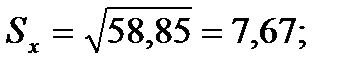
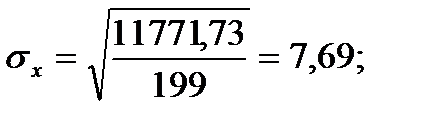
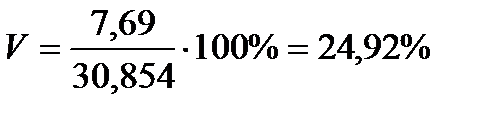
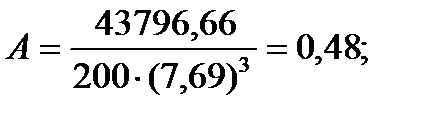
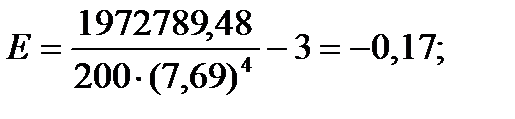
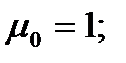
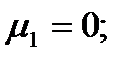
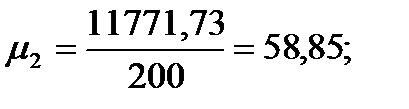
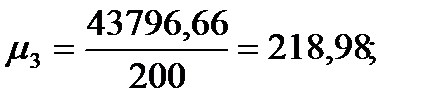
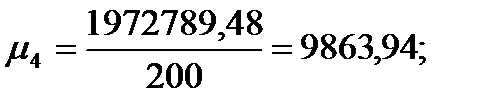
Высоты
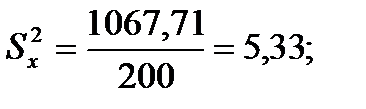
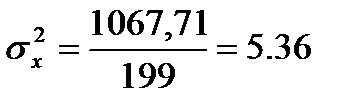
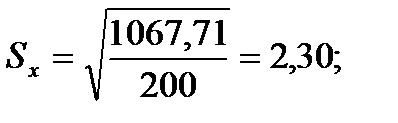
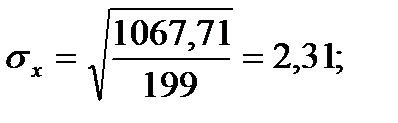
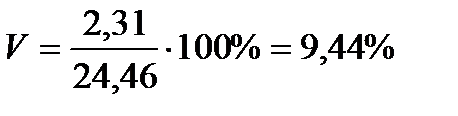
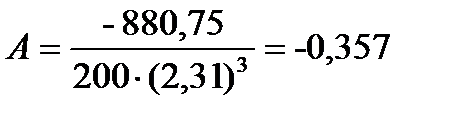
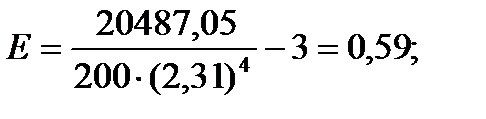
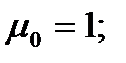
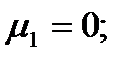
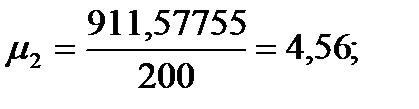
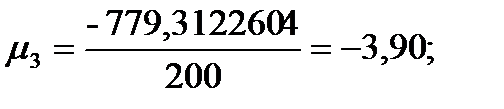
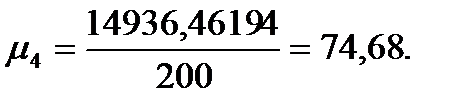
Для того чтобы определить точность полученных оценок статистических показателей, вычислим их стандартные ошибки:
Диаметры: Высоты:
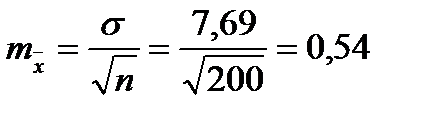
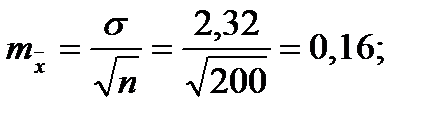
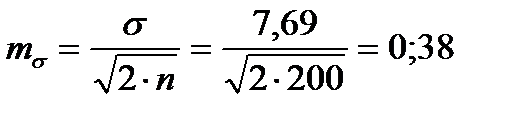
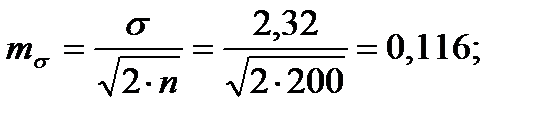
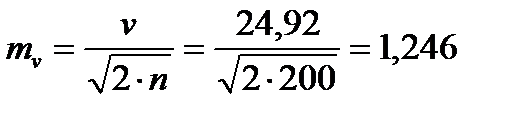
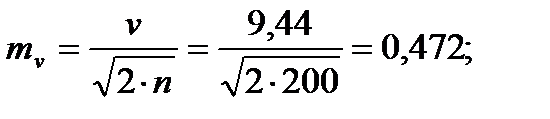
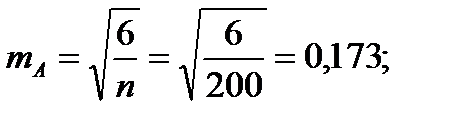
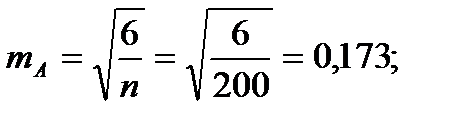
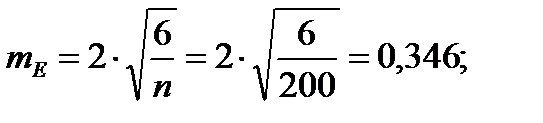
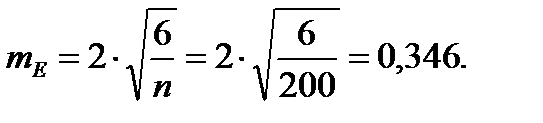
Чтобы сравнивать точность оценки среднего для объектов, имеющих разную размерность, часто используют показатель точности, который представляет собой стандартную ошибку оценки среднего, выраженную в процентах от самой средней величины. Вычислим показатель точности для рассматриваемого примера:
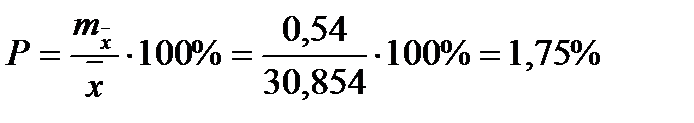 -диаметры;
-диаметры;
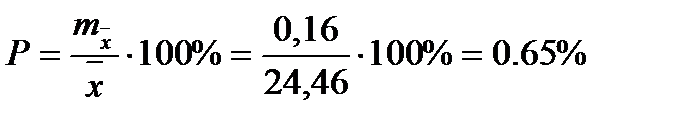 -высоты.
-высоты.



 ,
, —частота i-го класса. Средняя арифметическая величина, вычисленная по формуле, называется - взвешенной.
—частота i-го класса. Средняя арифметическая величина, вычисленная по формуле, называется - взвешенной.

 — площадь сечения i-го дерева; dt —диаметр i-го дерева,
— площадь сечения i-го дерева; dt —диаметр i-го дерева, 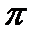 = 3,14;
= 3,14;  - среднеквадратический диаметр древостоя.
- среднеквадратический диаметр древостоя. см
см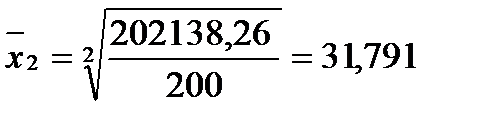 см
см
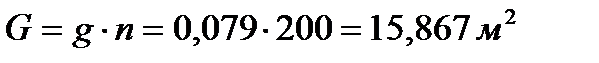
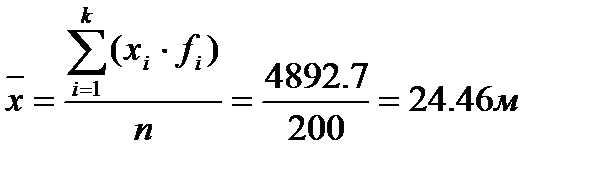

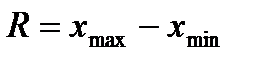

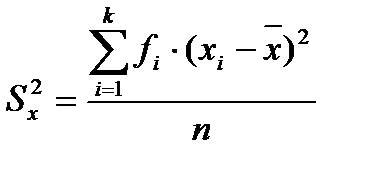 ,
,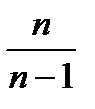 , называемый поправкой Бесселя:
, называемый поправкой Бесселя: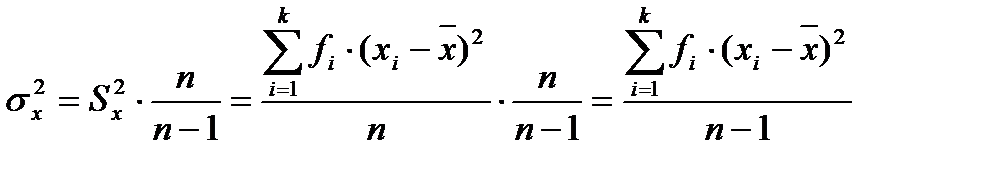 ,
,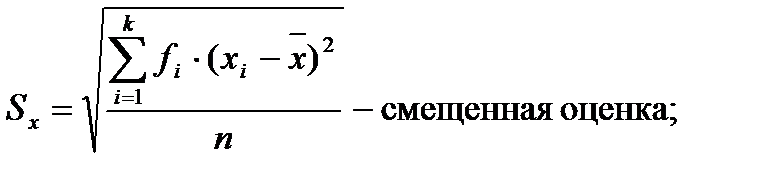
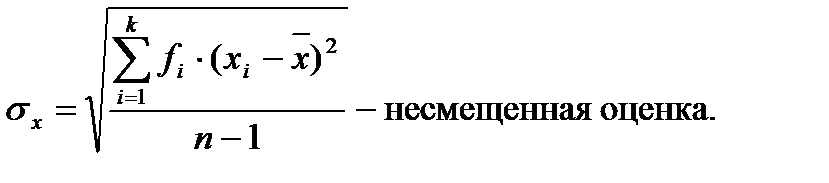
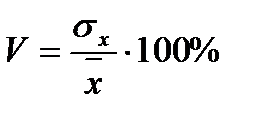
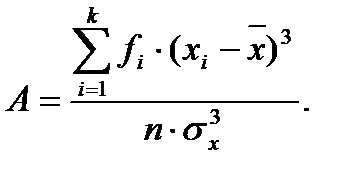
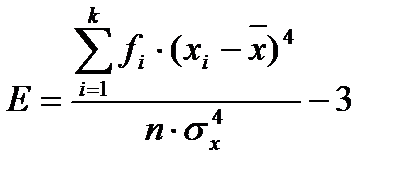
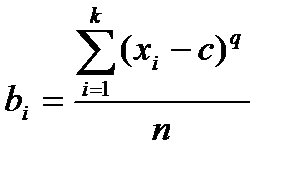 ,
,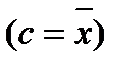 , называются центральными:
, называются центральными: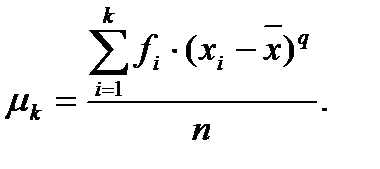
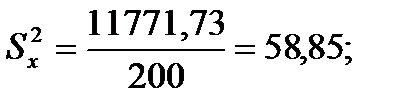
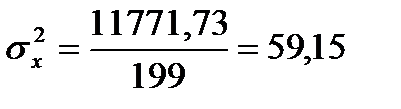
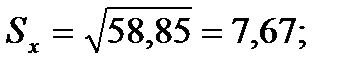
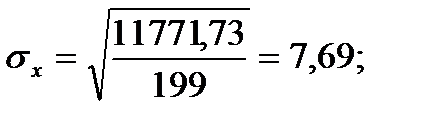
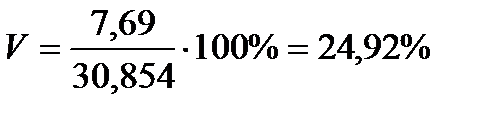
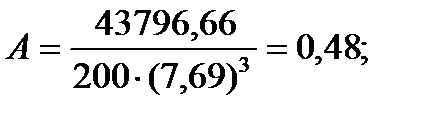
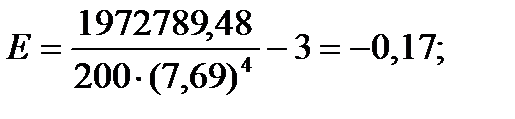
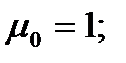
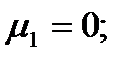
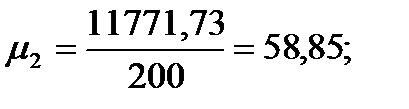
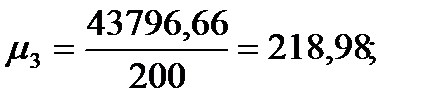
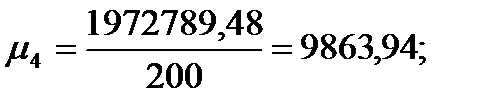
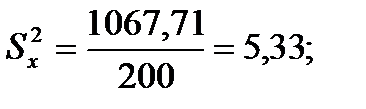
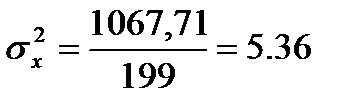
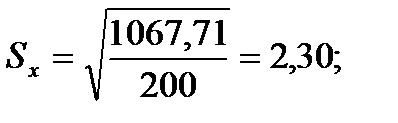
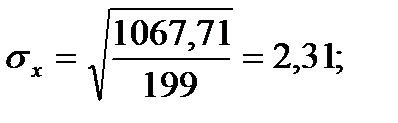
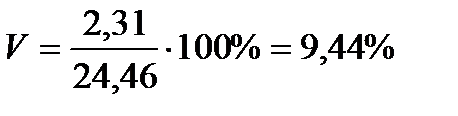
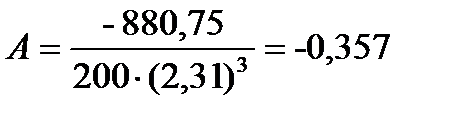
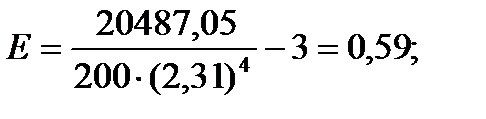
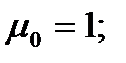
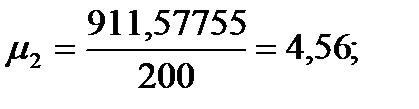
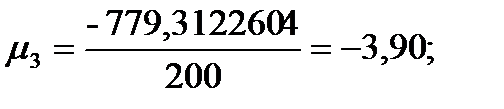
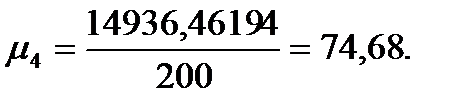
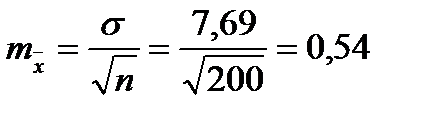
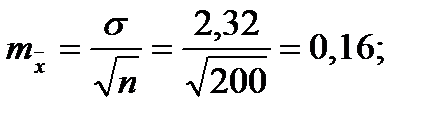
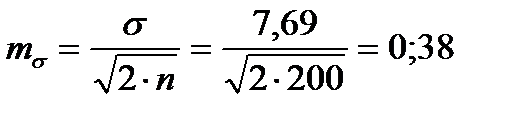
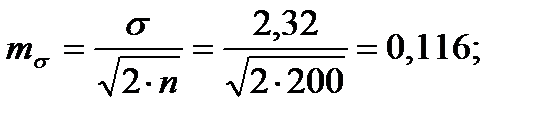
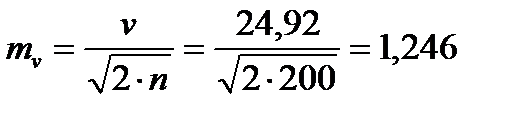
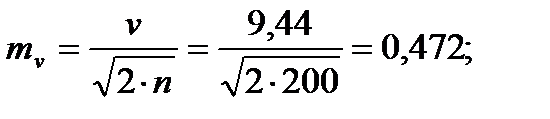
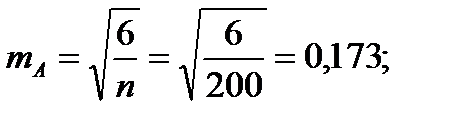
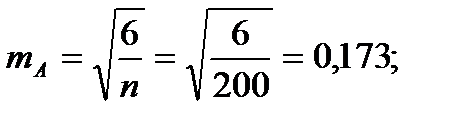
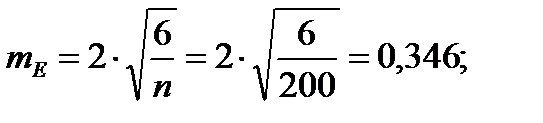
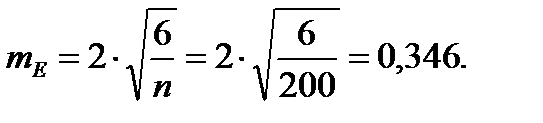
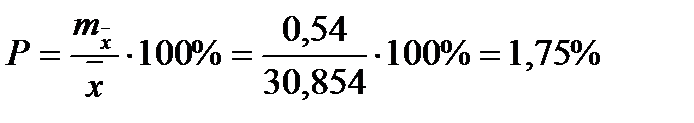 -диаметры;
-диаметры;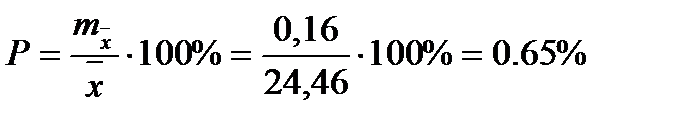 -высоты.
-высоты.

