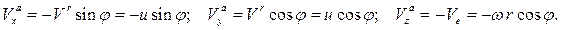Напомним теорему сложения скоростей при сложном движении точки:
абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:
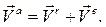
Теорема сложения ускорений при сложном движении точки имеет вид:
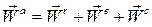 ,
,
где вектор
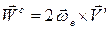
называется ускорением Кориолиса.
Таким образом,
абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений.
Пример 3.3
Круглая трубка радиуса 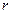 вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси 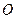 по часовой стрелке с постоянной угловой скоростью
по часовой стрелке с постоянной угловой скоростью  . Внутри трубки около ее точки
. Внутри трубки около ее точки  колеблется шарик
колеблется шарик 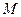 , причем так, что
, причем так, что  (Рис. 3.5). Определить скорость, касательное и нормальное ускорения в абсолютном движении шарика в любой момент времени.
(Рис. 3.5). Определить скорость, касательное и нормальное ускорения в абсолютном движении шарика в любой момент времени.

|
|
|
| Рис.3.5
|
Относительное движение шарика представляет собой движение по окружности радиуса 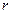 с центром в точке
с центром в точке 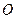 по закону
по закону  . Определим закон изменения дуговой координаты шарика в относительном движении:
. Определим закон изменения дуговой координаты шарика в относительном движении:

Вычислим относительную скорость и относительное ускорение шарика:



Трубка сообщает шарику переносную скорость

и переносное ускорение

Угол между осью вращения трубки, вдоль которой направлен вектор ее угловой скорости, и вектором относительной скорости шарика равен 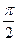 , так что
, так что

Для определения направления ускорения Кориолиса удобнее всего воспользоваться правилом Жуковского.
Абсолютная траектория шарика в данном случае очевидна – это все та же окружность с центром 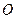 радиуса
радиуса 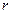 . Используя теорему сложения скоростей, получаем:
. Используя теорему сложения скоростей, получаем:
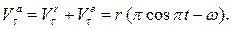
Используя теорему Кориолиса (3.12), получаем:
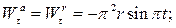

Направления векторов указаны на Рис. 3.5. Ускорение Кориолиса и относительная скорость представлены на рисунке для случая 
Пример 3.4
Лопатка 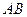 рабочего колеса турбины, вращающегося против хода часовой стрелки замедленно с угловым ускорением
рабочего колеса турбины, вращающегося против хода часовой стрелки замедленно с угловым ускорением  , имеет радиус кривизны 0.2 м и центр кривизны в точке
, имеет радиус кривизны 0.2 м и центр кривизны в точке 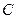 , причем
, причем  м. Частица воды
м. Частица воды 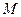 , отстоящая от оси
, отстоящая от оси 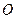 турбины на расстоянии 0.2 м, движется по лопатке наружу и имеет скорость 0.25 м/с и касательное ускорение 0.5 м
турбины на расстоянии 0.2 м, движется по лопатке наружу и имеет скорость 0.25 м/с и касательное ускорение 0.5 м  по отношению к лопатке. Определить абсолютное ускорение частицы
по отношению к лопатке. Определить абсолютное ускорение частицы 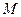 в тот момент времени, когда угловая скорость турбины равна 2 рад/с.
в тот момент времени, когда угловая скорость турбины равна 2 рад/с.
Подвижную систему координат свяжем с рабочим колесом турбины (Рис. 3.6). Относительной траекторией частицы воды является кривая 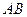 – лопатка турбины. Определим нормальное ускорение точки
– лопатка турбины. Определим нормальное ускорение точки 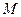 в относительном движении
в относительном движении

Точка 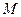 турбины описывает окружность с центром
турбины описывает окружность с центром 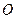 радиуса
радиуса  . Определим переносное ускорение точки:
. Определим переносное ускорение точки:

Направление ускорения Кориолиса определяем по правилу Жуковского. Модуль ускорения Кориолиса равен

Используя теорему Кориолиса, найдем проекции абсолютного ускорения частицы 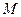 на оси подвижной системы координат (Рис. 3.6):
на оси подвижной системы координат (Рис. 3.6):



|
|

|
|
|
|
|
| Рис. 3.6
|
| Рис. 3.7
|
Остается определить  и
и  . Для этого используем теорему косинусов (Рис. 3.7):
. Для этого используем теорему косинусов (Рис. 3.7):

Отсюда
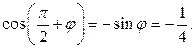
Таким образом,
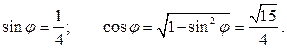
Окончательно получаем:

Пример 3.5
Диск радиуса 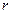 вращается вокруг неподвижной оси
вращается вокруг неподвижной оси  с постоянной угловой скоростью
с постоянной угловой скоростью  . По ободу диска движется точка
. По ободу диска движется точка 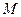 , имея относительно диска постоянную по модулю скорость
, имея относительно диска постоянную по модулю скорость 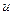 . Определить абсолютную скорость и абсолютное ускорение точки
. Определить абсолютную скорость и абсолютное ускорение точки 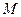 .
.
Подвижную систему отсчета связываем с диском (Рис. 3.8). По отношению к диску, т.е. в относительном движении, точка 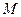 движется равномерно со скоростью
движется равномерно со скоростью 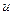 , описывая окружность радиуса
, описывая окружность радиуса 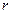 с центром в точке
с центром в точке 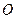 . Определяем относительное ускорение точки:
. Определяем относительное ускорение точки:

Рассмотрим переносное движение – его совершает диск. Точка 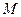 диска описывает окружность с центром
диска описывает окружность с центром 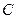 , плоскость которой параллельна координатной плоскости
, плоскость которой параллельна координатной плоскости 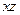 . Переносная скорость
. Переносная скорость

направлена по касательной к этой окружности в сторону вращения диска, т.е. перпендикулярно плоскости диска в отрицательном направлении координатной оси  . Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение:
. Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение:
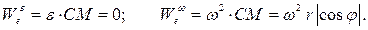
Вектор ускорения Кориолиса точки 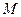 направлен перпендикулярно плоскости чертежа, в которой расположены векторы
направлен перпендикулярно плоскости чертежа, в которой расположены векторы 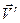 и
и 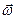 , причем, в ту сторону, откуда кратчайшее совмещение направления вектора
, причем, в ту сторону, откуда кратчайшее совмещение направления вектора 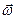 с направлением вектора
с направлением вектора 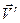 видно против хода часовой стрелки. В указанном на Рис. 3.9 положении точки
видно против хода часовой стрелки. В указанном на Рис. 3.9 положении точки 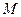 вектор ускорения Кориолиса направлен на нас, т.е. параллелен координатной оси
вектор ускорения Кориолиса направлен на нас, т.е. параллелен координатной оси  в положительную сторону этой оси. На Рис. 3.9 это направление условно обозначено острием стрелки, заключенным в кружок. Модуль ускорения Кориолиса вычисляется по формуле:
в положительную сторону этой оси. На Рис. 3.9 это направление условно обозначено острием стрелки, заключенным в кружок. Модуль ускорения Кориолиса вычисляется по формуле:
 .
.
|
|

|
|
|
|
|
| Рис.3.8
|
| Рис.3.9
|
| | | | |
При перемещении точки 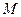 по диску направление ускорения Кориолиса не будет изменяться до тех пор, пока
по диску направление ускорения Кориолиса не будет изменяться до тех пор, пока  , т.е. пока
, т.е. пока  (точка
(точка 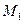 ). При пересечении точкой
). При пересечении точкой 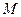 координатной оси
координатной оси 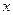 ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при
ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при  , проекция ускорения Кориолиса на направление оси
, проекция ускорения Кориолиса на направление оси  становится отрицательной и вектор
становится отрицательной и вектор  направлен от нас (точки
направлен от нас (точки  и
и  ).
).
Таким образом,

Используя теорему сложения скоростей

находим проекции вектора абсолютной скорости на оси подвижной системы координат:

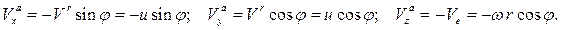

Используя теорему Кориолиса

находим проекции абсолютного ускорения точки на оси подвижной системы координат:




Примечание.
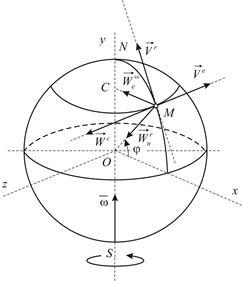
Последняя задача позволяет проиллюстрировать некоторые явления, связанные с вращением Земли, в частности, размыв берегов рек. Как видно, вращение Земли приводит к возникновению у частиц воды кориолисова ускорения, направленного перпендикулярно линии берегов. Наличие такого ускорения приводит к тому, что в северном полушарии дополнительно подмывается правый берег, который на прямолинейных участках рек заметно выше левого берега. В южном полушарии более высокий левый берег. Это явление в географии отражено в законе Бэра.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 22.10; 22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19; 23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-23;
СР-24; СР-25.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ:
- После практического занятия №7(15) проводится тест «МОДУЛЬ КБ».
ЛИТЕРАТУРА:
- Антонов В.И., Белов В.А., Егорычев О.О., Степанов Р.Н. //Курс теоретической механики (теория и практика) – М.: Архитектура – С, 2011 г.
- Мещерский И.В.// Сборник задач по теоретической механике. – Спб.: Лань, 2010 г.



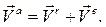
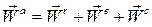 ,
,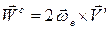
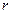 вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси 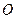 по часовой стрелке с постоянной угловой скоростью
по часовой стрелке с постоянной угловой скоростью  . Внутри трубки около ее точки
. Внутри трубки около ее точки  колеблется шарик
колеблется шарик 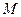 , причем так, что
, причем так, что  (Рис. 3.5). Определить скорость, касательное и нормальное ускорения в абсолютном движении шарика в любой момент времени.
(Рис. 3.5). Определить скорость, касательное и нормальное ускорения в абсолютном движении шарика в любой момент времени.






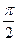 , так что
, так что
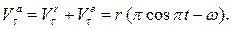
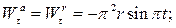


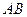 рабочего колеса турбины, вращающегося против хода часовой стрелки замедленно с угловым ускорением
рабочего колеса турбины, вращающегося против хода часовой стрелки замедленно с угловым ускорением  , имеет радиус кривизны 0.2 м и центр кривизны в точке
, имеет радиус кривизны 0.2 м и центр кривизны в точке 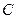 , причем
, причем  м. Частица воды
м. Частица воды  по отношению к лопатке. Определить абсолютное ускорение частицы
по отношению к лопатке. Определить абсолютное ускорение частицы 
 . Определим переносное ускорение точки:
. Определим переносное ускорение точки:





 и
и  . Для этого используем теорему косинусов (Рис. 3.7):
. Для этого используем теорему косинусов (Рис. 3.7):
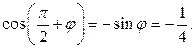
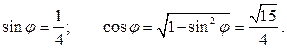

 с постоянной угловой скоростью
с постоянной угловой скоростью 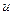 . Определить абсолютную скорость и абсолютное ускорение точки
. Определить абсолютную скорость и абсолютное ускорение точки 
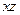 . Переносная скорость
. Переносная скорость
 . Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение:
. Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение: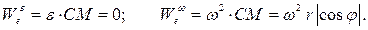
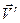 и
и 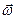 , причем, в ту сторону, откуда кратчайшее совмещение направления вектора
, причем, в ту сторону, откуда кратчайшее совмещение направления вектора  .
.

 , т.е. пока
, т.е. пока  (точка
(точка 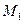 ). При пересечении точкой
). При пересечении точкой 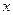 ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при
ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при  , проекция ускорения Кориолиса на направление оси
, проекция ускорения Кориолиса на направление оси  направлен от нас (точки
направлен от нас (точки  и
и  ).
).