Под элементарным конечным автоматом понимается автомат обладающий следующими свойствами:
- описывается как автомат Мура;
- входной и выходной алфавиты двоичны;
- имеет два внутренних состояния;
- обладают полной системой переходов;
- обладают полной системой выходов;
Говорят, что автомат обладает полной системой переходов, если для каждой пары внутренних состояних состояний автомата Si и Sj (i≠j) найдется хотя бы один входной сигнал, который переводит его из состояния Si в состояние Sj.
Для элементарного автомата, имеющего два внутренних состояния, полная система переходов выглядит следующим образом (табл.3.10):
| si si
|
| 0 → 0
|
| 0 → 1
|
| 1 → 0
|
| 1 → 1
|
Табл. 3.10
Если в каждом состоянии автомат имеет выходной сигнал отличный от выходных сигналов других состояний, то такой автомат обладает полной системой выходов.
С помощью элементарных автоматов можно, синтезировать конечный автомат любой сложности.
Для того, чтобы синтезировать конечный автомат любой сложности, необходимо иметь хотя бы один тип элементарного автомата и фуекционально полный набор логических элементов.
Учитывая, что выходной сигнал автомата Мура совпадает с его состоянием, то нет необходимости составлять таблицу выходов.
Работа реальных автоматов описывается однозначными операторами, т.е. такими которые любой паре символов x(t) и Sk(t) ставят в однозначное соответствие пару yj(t+1) и Sk(t+1). Такие операторы называются детерменированными, а соответствующие им автоматы – автоматами с детерменированной системой переходов или просто детерменнированными автоматами.
В вычислительной технике в качестве элементарных автоматов чаще всего используются триггерные схемы (триггеры).
Триггеры различаются по числу входов.
Существуют только четыре типа элементарных автоматов, которые имеют детерменированную и полную систему переходов. (табл.3.11-3.14)
|
|
|
|
|
|
|
|
| x(t)
| s(t)
| s(t+1)
|
| x(t)
| s(t)
| s(t+1)
|
| x(t)
| s(t)
| s(t+1)
|
| x(t)
| s(t)
| s(t+1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл. 3.11
Табл. 3.12
Табл. 3.13
Табл. 3.14
Таблицы 3.11 и 3.12, 3.7 и 4.9 различаются только способом кодирования входных сигналов и состояний S(t+1). Следовательно, автоматы, заданные соответствующими таблицами, изоморфны. Таким образом имеется лишь два принципиально различных элементарных автомата с одним входом. Примем за их описание таблицы 3.11 и 3.12.
Рассмотрим элементарный автомат описанный таблицей 3.11, где состояние автомата в следующий момент времени S(t+1) совпадает с входным сигналом x(t). Так как S(t+1) в автоматах Мура отождествляется с выходным сигналом, то выходные сигналы для этого элементарного автомата представляют собой задержанные на один такт входные сигналы, а сам автомат – элемент задержки на один такт. Такой автомат называется триггером типа D. Получим функцию переходов этого триггера:
S(t+1)=x(t)S’(t)+x(t)S(t)=x(t)
Элементарный автомат, описанный в табл.3.12 меняет свое состояние только при подаче на его вход сигнала x(t)=1. Его функция переходов запишется в виде
S(t+1)=x’(t)S(t)+x(t)S’(t)=x(t)+S(t).
Как видим из этой записи функция выходов равна сложению по mod2 входного сигнала x(t) и состояния автомата S(t) в этот же момент времени. Такой элементарный автомат называется триггером со счетным входом или триггером типа Т.
На рис. 3.4 а, б. приведены схемотехнические изображения триггеров типа D и Т соответственно:

Рис.3.4. Графическое изображение триггеров D (рис.3.4 а) и триггера Т (рис.3.4 б).
В схемотехнике принятии выходов триггера обозначать через Q(t) и для каждого триггера изображать как прямой выход триггера Q(t) так и интерверсию этого выхода Q(t).
В современных средствах вычислительной техники широкое применение получили элементарные автоматы с двумя входами xo(t) и x1(t), функционирующие следующим образом: если на вход xo(t) действует сигнал, равный нулю, а на вход x1(t) – сигнал равный единице, то автомат переходит в состояние единица, независимо от его состояния в предыдущий момент времени. Поэтому вход xo(t) называют нулевым, а x1(t) – единичным сигналом.
В общем случае элементарный автомат с двумя входами, задаваемый описанным выше способом, имеет полную детерменированную систему переходов (табл.3.15).
Таб. 3.15
| x0(t)
| x1(t)
| s(t)
| s(t+1)
|
|
|
|
| -
|
|
|
|
| -
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -
|
|
|
|
| -
|
При различных схемных реализациях элементарных автоматов с двумя входами запрещенными комбинациями входных сигналов являются либо комбинация xo(t)=x1(t)=0, либо комбинация xo(t)=x1(t)=1. Если на оба входа такого триггера действуют сигналы, равные нулю (единице), то работа схемы в большинстве случаев, будет неустойчивой, а следующее состояние неопределенным.
Триггеры типа RS (триггеры с разделенными входами).
Входы такого триггера принято обозначать через S(set) – «единичный» вход, и R (reset) – «нулевой» вход.
Для R-S триггера подача одновременно на оба входа сигнала равного единице (нулю) – запрещена. Два варианта (в зависимости от реализации) триггера R-S приведены в таблицах 3.16.и 3.17.
Табл.(3.16) Табл.(3.17)
| R(t)
| S(t)
| Q(t)
| Q(t+1)
|
| R(t)
| S(t)
| Q(t)
| Q(t+1)
|
|
|
|
|
|
|
|
|
| -
|
|
|
|
|
|
|
|
|
| -
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -
|
|
|
|
|
|
|
|
|
| -
|
|
|
|
|
|
Запишем функции выходов в аналитической форме и минимизируем их для обеих вариантов таблице 3.16 и 3.17.
Для варианта а, с учетом запрещенных комбинаций <R(t)S(t)Q’(t);R(t)S(t)Q(t)>, функция выходов запишется в следующем виде Q(t+1)=R’(t)S’(t)Q(t)+R’(t)S(t)Q’(t)+R’(t)S(t)Q(t). нанесем полученную функцию на карту Вейча и минимизируем ее (табл 3.18)
Табл. 3.18
S(t) Q(t+1)=S(t)+R(t)Q(t).
Q(t)
При реализации этого триггера по второму варианту, функция выходов запишется в виде Q(t+1)=R’(t)S(t)Q’(t)+R’(t)S(t)Q(t)+R(t)S(t)Q(t), при запрещенных комбинациях <R’(t)S’(t)Q’(t);R’(t)S’(t)Q(t)>. Карта Вейча для минимизации такой функции приведена в таблице (3.19).
Табл. 3.19
S(t) Q(t+1)=R(t)+S(t)Q(t).
Q(t)
Таблицу триггера можно записать в сокращенном виде (табл.3.20)
Табл.3.20
a b
| Q(t) → Q(t+1)
| R(t)
| S(t)
|
| Q(t) → Q(t+1)
| R(t)
| S(t)
|
| 0 → 0
| b1
|
|
| 0 → 0
|
| b1
|
| 0 → 1
|
|
|
| 0 → 1
|
|
|
| 1 → 0
|
|
|
| 1 → 0
|
|
|
| 1 → 1
|
| b2
|
| 1 → 1
| b2
|
|
Приведем пояснения о правилах, по которым были построена таблица (3.20а)
Переходы триггера R-S при переходе его состояния из нуля в ноль и из единицы в единицу продублированы. Поэтому при переходе из нуля в ноль (табл.20а) на вход S(t) требуется подать обязательно ноль, а на вход R(t) можно подать либо ноль, либо единицу. Поэтому в соответствующем месте таблицы поставлено b1, которое при минимизации функции выходов Q(t+1) ей может быть присвоено значение, как ноль, так и единица. Аналогично, при переходе триггера из единицы в единицу на входе S(t) можно подать как ноль, так и еденицу.
По такому же принципу составлена и таблица 3.20б.
Будем изображать триггер так, как показано на рис.3.5
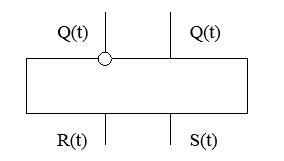
Рис. 3.5 Схематехническое изображение триггера R-S.
Триггер типа j-k, называемый триггером с диблированными переходами, аналогичен триггеру типа R-S, но с той разницей, что для него допускается комбинация входных сигналов j(t)=k(t)=1. В этом случае триггер меняет свое состояние на инверсное. В таблице 3.21 приведена таблица переходов j-k триггера.
Табл. 3.21
Отметим, сто триггер j-k называют триггером дублированных переходов, т.к. любой переход из Q(t) в Q(t+1) дублирован. Запишем функцию переходов j-k триггера.
Q(t+1)=j’(t)k(t)Q(t)+j(t)k’(t)Q’(t)+j(t)k’(t)Q(t)+j(t)k(t)Q’(t).
Нанесем функцию на карту Вейча и минимизируем ее. (табл 3.22)
Табл. 3.22
k(t)
Q(t)
В результате минимизации получаем Q(t+1)=j(t)Q’(t)+k’(t)Q(t).
Составим сокращенную таблицу переходов j-k триггера (табл. 3.23)
Табл.3.23
| Q(t) → Q(t+1)
| j(t)
| k(t)
|
| 0 → 0
|
| b1
|
| 0 → 1
|
| b2
|
| 1 → 0
| b3
|
|
| 1 → 1
| B4
|
|










