Уравнение Лапласа в сферических координатах в случае сферически симметричной задачи сводится к обыкновенному дифференциальному уравнению
 (42)
(42)
Интегрируя это уравнение, находим
 (43)
(43)
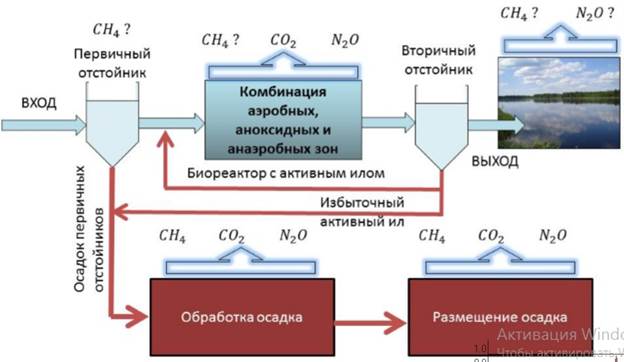
где С 1и С 2 – произвольные постоянные. С точностью до констант С 1и С 2 эта функция совпадает с полем точечного заряда е, помещенного в начале координат, т.е.  . Функцию
. Функцию  иногда называют фундаментальным решением уравнения Лапласа в пространстве 1). Строго говоря, поскольку к указанному решению можно всегда добавить произвольную гармоническую функцию φ (r), фундаментальным решением уравнения Лапласа можно назвать2) и функцию
иногда называют фундаментальным решением уравнения Лапласа в пространстве 1). Строго говоря, поскольку к указанному решению можно всегда добавить произвольную гармоническую функцию φ (r), фундаментальным решением уравнения Лапласа можно назвать2) и функцию
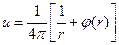 (44)
(44)
(45) Аналогичным образом для задач, обладающих цилиндрической или круговой симметрией можно получить и фундаментальное решение уравнения Лапласа на плоскости
 (45)
(45)
Гармонические функции.
Функции, являющиеся решением уравнения Лапласа, обладают целым рядом общих (примечательных) свойств, благодаря чему их выделяют в отдельный класс и называют гармоническими функциями при выполнении нескольких условий. Говорят, что в точке x функция u (x) является гармонической (или гармонична), если в этой точке она
1) имеет непрерывные вторые производные и удовлетворяет уравнению Лапласа. Говорят, что функция u (x) является гармонической (или гармонична), в замкнутой области D, если она непрерывна в этой области;
2) гармонична во всех внутренних точках;
3) когда область бесконечна, стремится к нулю при стремлении точки x к бесконечно удаленной точке вдоль любого луча, принадлежащего области. непрерывна в этой области;
4) гармонична во всех внутренних точках;
5) когда область бесконечна, стремится к нулю при стремлении точки x к бесконечно удаленной точке вдоль любого луча, принадлежащего области. непрерывна в этой области;
6) гармонична во всех внутренних точках;
7) когда область бесконечна, стремится к нулю при стремлении точки x к бесконечно удаленной точке вдоль любого луча, принадлежащего области.
В силу этого определения регулярные решения граничных задач для уравнения Лапласа являются функции, гармоничными в рассматриваемой области.
Для гармонических функций двух переменных оказывается целесообразным введение понятия сопряженных функций. Гармонические функции двух переменных u (x, y) и v (x, y) называются сопряженными, если они связаны между собой условиями Коши Римана, а именно
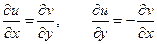 (46)
(46)
1)Тихонов и Самарский, с. 282
2) Кошляков и др., с. 268
Выполнение этих условий приводит к выводу, что функция комплексного переменного  , составленная как
, составленная как  представляет собой аналитическую функцию.
представляет собой аналитическую функцию.
Если n, s – прямоугольная система координат, получающаяся из системы координат x, y путем поворота и переноса начала координат, то условия (46) запишутся в виде

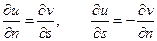
Из этих равенств следует, что если на некотором замкнутом контуре С для функции v известна производная по нормали  , то для функции u будет известна производная по касательной
, то для функции u будет известна производная по касательной  .
.
Это свойство сопряженных гармонических функций двух переменных позволяет вторую краевую задачу для области D
 , (47)
, (47)
где ζ – точка на контуре С, свести к решению первой краевой задачи для сопряженной функции u в той же области
где ζ – точка на контуре С, свести к решению первой краевой задачи для сопряженной функции u в той же области
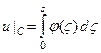 (48)
(48)
Важной особенностью гармонических функций является их свойство принимать максимальное и минимальное значения только на границе области. Это свойство устанавливает теорема о максимуме и минимуме, которая формулируется следующим образом.
Т е о р е м а. Если функция u (x)гармонична в области D, то она не имеет внутри этой области ни максимумов, ни минимумов, достигая своих наибольшего и наименьшего значений на её границе.
Доказательство проведем от обратного. Предположим, что функция u в некоторой внутренней точке x имеет максимум. Опишем из точки x, как из центра, сферу σ, лежащую целиком внутри области D. Радиус поверхности σ можно выбрать сколь угодно малым, лишь бы выполнялось неравенство
 , (49)
, (49)
где u н – наибольшее значение u на поверхности сферы σ, а ε > 0. Далее, можно найти такое достаточно малое число η > 0, чтобы для любой точки ξ, лежащей на или внутри поверхности σ, было
 , (50)
, (50)
где  – расстояние между точками x и ξ. Тогда в силу неравенства (49), функция
– расстояние между точками x и ξ. Тогда в силу неравенства (49), функция
 (51)
(51)
в точке  будет превосходить свое наибольшее значение на поверхности σ. Это означает, что её максимум должен достигаться внутри поверхности σ. Однако в точке максимума вторые производные по координатам точки ξ не могут быть больше нуля. Между тем
будет превосходить свое наибольшее значение на поверхности σ. Это означает, что её максимум должен достигаться внутри поверхности σ. Однако в точке максимума вторые производные по координатам точки ξ не могут быть больше нуля. Между тем
 . (52)
. (52)
Противоречие доказывает невозможность неравенства (49), откуда следует, что функция u внутри области D не может иметь максимума. Аналогичным образом можно показать, что функция u не может иметь и минимума внутри области D. В то же время, будучи непрерывной функцией, она должна (по теореме Вейерштрасса)достигать своего наибольшего и наименьшего значений в области D. Так как это невозможно внутри области, то эти значения достигаются функцией u на границе области.
Доказанная теорема имеет весьма полезное следствие.
С л е д с т в и е. Если функции u и v гармоничны в области D, то выполнение на границе области одного из неравенств
 или
или  (53)
(53)
влечет за собой выполнение этого же неравенства и внутри области.
В самом деле, если функция (u - v), гармоническая в области D, неположительна на границе области, т.е. u – v ≤ 0, то она неположительна и всюду в области, так как внутри области она не может превзойти свое значение на границе. Отсюда следует исходное утверждение в отношении неравенства  . Что касается неравенства
. Что касается неравенства  , то оно эквивалентно двум неравенствам:
, то оно эквивалентно двум неравенствам:  и
и 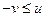 . Согласно уже доказанному, выполнение каждого из них на границе влечет за собой их выполнение и внутри области. Отсюда следует доказанность сформулированного следствия полностью.
. Согласно уже доказанному, выполнение каждого из них на границе влечет за собой их выполнение и внутри области. Отсюда следует доказанность сформулированного следствия полностью.
Формулы Грина
Важной формулой для изучения гармонических функций является так называемая основная формула Грина, которая вытекает, как мы сейчас убедимся, последовательно из первой и второй формул Грина. Сами формулы Грина являются прямым следствием формулы Остроградского при некоторых дополнительных условиях.
Как известно, формула Остроградского записывается следующим образом
 (54)
(54)
где T – некоторый объем, ограниченный достаточно гладкой поверхностью S,
P, Q, R – произвольные, непрерывно дифференцируемые функции,
α, β, γ – углы внешней нормали n к поверхности S с координатными осями.
Если теперь рассматривать функции P, Q, R как компоненты некоторого вектора  , то мы получим формулу Гаусса-Остроградского
, то мы получим формулу Гаусса-Остроградского
 (55)
(55)
Далее перейдем к выводу формул Грина.
Пусть функции  и
и  непрерывны вместе со своими первыми производными внутри
непрерывны вместе со своими первыми производными внутри 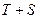 и имеют непрерывные вторые производные внутри Т.
и имеют непрерывные вторые производные внутри Т.
Положим

т.е.  . Подставляя теперь выражения для P, Q и R в формулу (55), получим
. Подставляя теперь выражения для P, Q и R в формулу (55), получим
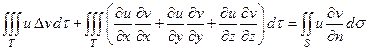 (56)
(56)
Учитывая, что
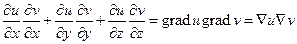 ,
,
и перенося второй интеграл в правую часть, мы можем переписать формулу (56) в виде
 (57)
(57)
Эта формула и носит название первой формулы Грина.
Меняя местами u и v, будем иметь
 (58)
(58)
Вычитая равенство (58) из равенства (57), пучаем вторую формулу Грина
 (59)
(59)
Полученные формулы Грина применимы и в том случае, когда область Т ограничена несколькими поверхностями. Это пригодится нам при выполнении следующего шага и, кроме того, важно при решении практических задач.
В том случае, когда u и v являются функциями двух переменных, функции Грина имеют аналогичный вид. При этом интеграл по объему заменяется за интеграл по площади области S, на которой заданы u и v, а интеграл по поверхности на интеграл по контуру С, ограничивающему эту область:
 .
.
Пусть теперь 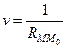 , где М 0 – некоторая внутренняя точка области. Как мы выяснили в предыдущем параграфе, эта функция удовлетворяет уравнению Лапласа при
, где М 0 – некоторая внутренняя точка области. Как мы выяснили в предыдущем параграфе, эта функция удовлетворяет уравнению Лапласа при  , но, поскольку она имеет разрыв в точке М 0 , то непосредственно применить вторую формулу Грина в области Т нельзя. Однако, если выделить область K ε, ограниченную сферой S ε радиуса ε с центром в точке М 0 , то в области Т – K ε функция v будет непрерывна и можно воспользоваться формулой (59) и записать
, но, поскольку она имеет разрыв в точке М 0 , то непосредственно применить вторую формулу Грина в области Т нельзя. Однако, если выделить область K ε, ограниченную сферой S ε радиуса ε с центром в точке М 0 , то в области Т – K ε функция v будет непрерывна и можно воспользоваться формулой (59) и записать
 (60)
(60)
Поскольку в области Т – K ε функция 1/ R удовлетворяет уравнению Лапласа, то под интегралом в левой части останется только второе слагаемое

В правой части этого равенства только два последних интеграла зависят от ε. Вычисляя производную по внешней нормали к области Т – K ε на поверхности S ε, получим
 ,
,
откуда

Пользуясь для вычисления интеграла в правой части теоремой о среднем, получим

где uср – среднее значение функции u (M) на поверхности S ε.
Аналогичным образом преобразуем третий интеграл

Устремим теперь радиус ε к нулю, тогда получим
во-первых,  , так как u (M) – непрерывная функция, uср – её среднее значение по сфере радиуса ε с центром в точке М 0 ;
, так как u (M) – непрерывная функция, uср – её среднее значение по сфере радиуса ε с центром в точке М 0 ;
во-вторых,  , так как из непрерывности первых производных функции u (M) внутри Т вытекает ограниченность её производной по нормали в окрестности точки М 0 ;
, так как из непрерывности первых производных функции u (M) внутри Т вытекает ограниченность её производной по нормали в окрестности точки М 0 ;
в-третьих, по определению несобственного интеграла в левой части получим

Подставляя полученные выражения в формулу (60), можем окончательно переписать её и прийти к основной интегральной формуле Грина
 , (61)
, (61)
где Р – точка, лежащая на поверхности S.
Если же функция u является гармонической, то формула (61) примет вид
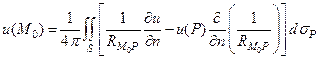 (62)
(62)
Таким образом, значение гармонической функции в любой внутренней точке области выражается через значение этой функции и её нормальной производной на поверхности области.
Отметим, что каждый из интегралов
 и
и  (63)
(63)
где μ и ν – непрерывные функции, является гармонической функцией вне поверхности S. В самом деле, так как все подынтегральные функции и их производные непрерывны вне поверхности S, то производные от интегралов (63) можно вычислить при помощи дифференцирования под знаком интеграла.
Отсюда вытекает важное следствие: всякая гармоническая функция внутри области гармоничности дифференцируема бесчисленное множество раз.



 (42)
(42) (43)
(43) . Функцию
. Функцию  иногда называют фундаментальным решением уравнения Лапласа в пространстве 1). Строго говоря, поскольку к указанному решению можно всегда добавить произвольную гармоническую функцию φ (r), фундаментальным решением уравнения Лапласа можно назвать2) и функцию
иногда называют фундаментальным решением уравнения Лапласа в пространстве 1). Строго говоря, поскольку к указанному решению можно всегда добавить произвольную гармоническую функцию φ (r), фундаментальным решением уравнения Лапласа можно назвать2) и функцию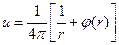 (44)
(44) (45)
(45)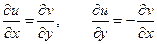 (46)
(46) , составленная как
, составленная как  представляет собой аналитическую функцию.
представляет собой аналитическую функцию.
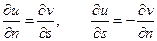
 , то для функции u будет известна производная по касательной
, то для функции u будет известна производная по касательной  .
. , (47)
, (47)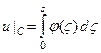 (48)
(48) , (49)
, (49) , (50)
, (50) – расстояние между точками x и ξ. Тогда в силу неравенства (49), функция
– расстояние между точками x и ξ. Тогда в силу неравенства (49), функция (51)
(51) будет превосходить свое наибольшее значение на поверхности σ. Это означает, что её максимум должен достигаться внутри поверхности σ. Однако в точке максимума вторые производные по координатам точки ξ не могут быть больше нуля. Между тем
будет превосходить свое наибольшее значение на поверхности σ. Это означает, что её максимум должен достигаться внутри поверхности σ. Однако в точке максимума вторые производные по координатам точки ξ не могут быть больше нуля. Между тем . (52)
. (52) или
или  (53)
(53)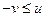 . Согласно уже доказанному, выполнение каждого из них на границе влечет за собой их выполнение и внутри области. Отсюда следует доказанность сформулированного следствия полностью.
. Согласно уже доказанному, выполнение каждого из них на границе влечет за собой их выполнение и внутри области. Отсюда следует доказанность сформулированного следствия полностью. (54)
(54) , то мы получим формулу Гаусса-Остроградского
, то мы получим формулу Гаусса-Остроградского (55)
(55) и
и  непрерывны вместе со своими первыми производными внутри
непрерывны вместе со своими первыми производными внутри 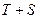 и имеют непрерывные вторые производные внутри Т.
и имеют непрерывные вторые производные внутри Т.
 . Подставляя теперь выражения для P, Q и R в формулу (55), получим
. Подставляя теперь выражения для P, Q и R в формулу (55), получим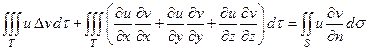 (56)
(56)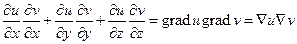 ,
, (57)
(57) (58)
(58) (59)
(59) .
.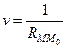 , где М 0 – некоторая внутренняя точка области. Как мы выяснили в предыдущем параграфе, эта функция удовлетворяет уравнению Лапласа при
, где М 0 – некоторая внутренняя точка области. Как мы выяснили в предыдущем параграфе, эта функция удовлетворяет уравнению Лапласа при  , но, поскольку она имеет разрыв в точке М 0 , то непосредственно применить вторую формулу Грина в области Т нельзя. Однако, если выделить область K ε, ограниченную сферой S ε радиуса ε с центром в точке М 0 , то в области Т – K ε функция v будет непрерывна и можно воспользоваться формулой (59) и записать
, но, поскольку она имеет разрыв в точке М 0 , то непосредственно применить вторую формулу Грина в области Т нельзя. Однако, если выделить область K ε, ограниченную сферой S ε радиуса ε с центром в точке М 0 , то в области Т – K ε функция v будет непрерывна и можно воспользоваться формулой (59) и записать (60)
(60)
 ,
,


 , так как u (M) – непрерывная функция, uср – её среднее значение по сфере радиуса ε с центром в точке М 0 ;
, так как u (M) – непрерывная функция, uср – её среднее значение по сфере радиуса ε с центром в точке М 0 ; , так как из непрерывности первых производных функции u (M) внутри Т вытекает ограниченность её производной по нормали в окрестности точки М 0 ;
, так как из непрерывности первых производных функции u (M) внутри Т вытекает ограниченность её производной по нормали в окрестности точки М 0 ;
 , (61)
, (61)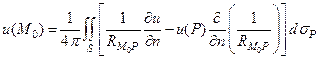 (62)
(62) и
и  (63)
(63)