Теперь мы покажем, что малые поперечные колебания мембраны описываются двумерным волновым уравнением (1). Мембраной называют тонкую пленку, которая находится в состоянии натяжения и не оказывает сопротивление изгибу и сдвигу. Покажем, что малые колебания мембраны описываются двумерным волновым уравнением.
Пусть бесконечная мембрана в положении равновесия расположена в плоскости (x,y) и находится под действием равномерного натяжения T, т.е. силы, приходящейся на единицу длины произвольного контура и направленной перпендикулярно этому контуру в каждой его точке. Будем также предполагать, что на мембрану параллельно оси 0u действует внешняя сила p (x, y, t), рассчитанная на единицу площади.
Будем рассматривать только поперечные смещения мембраны, при которых каждая её точка движется перпендикулярно плоскости (x,y). Смещения u каждой точки мембраны будут функцией координат этой точки x,y и времени t. Будем предполагать, что они настолько малы, что квадратами производных ux и uy можно пренебречь.
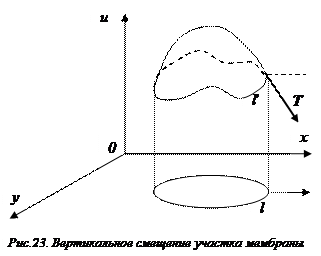
Выделим произвольный участок мембраны
σ, ограниченный кривой
l (Рис.3.1). В результате смещения этот участок деформируется и перейдет в некоторый участок
σ ', ограниченный контуром
l '. На этот участок в каждой его точке, в том числе и по контуру
l ' будет действовать равномерно распределенное натяжение
Т, лежащее в плоскости касательной к поверхности мембраны. Сила этого натяжения равна
Тdl ', где
dl ' – элемент дуги кривой
l '. Проекция силы
Т dl ' на ось
0u будет равна абсолютной величине
Тdl ', умноженной на косинус угла вектора
Т с осью
0u, который в силу нашего предположения о малости величины смещения будет равен
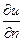
, где
n – внешняя нормаль к контуру
l.
В результате равнодействующая сил, приложенных к контуру l ' будет равна
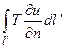
Поскольку при малых перемещениях мембраны можно считать 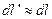 , то мы можем в записанном интеграле путь интегрирования dl 'заменить на dl. Тогда применяя формулу Грина, получим
, то мы можем в записанном интеграле путь интегрирования dl 'заменить на dl. Тогда применяя формулу Грина, получим
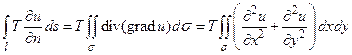 (46)
(46)
Суммарная внешняя сила, действующая на участок σ ', будет равна
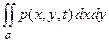 (47)
(47)
По второму закону Ньютона сумма сил (1) и (2) должна равняться интегралу
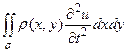 (48)
(48)
В результате получим
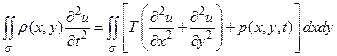 ,
,
Откуда в силу произвольности участка σ следует, что
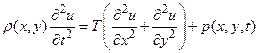 (49)
(49)
Это и есть уравнение малых поперечных колебаний мембраны. В случае, если мембрана однородная, полученное уравнение после некоторых переобозначений можно переписать следующим образом:
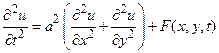 , (50)
, (50)
где
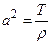 и
и 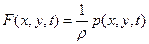
В более компактной форме уравнение (50) можно записать также в следующем виде:
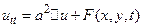 (51)
(51)
В качестве начальных условий для уравнения (50) или (51) задаются смещение и скорость любой её точки в начальный момент времени
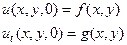 (52)
(52)
Граничные условия
В случае ограниченной мембраны наряду с начальными условиями (52) для уравнения (49) формулируются и граничные условия трех видов. В отличие от струны или стержня, границами являлись два противоположных конца, у мембраны границей является ограничивающий её плоский в исходном положении контур l.
В граничном условии первого рода задаются перемещения точек границы мембраны в любой момент времени, а именно
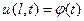 (53)
(53)
Если граница мембраны покоится, т.е. имеет место закрепление граница мембраны, то граничное условие (52) становится однородным
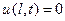 (54))
(54))
В граничном условии второго рода задаётся нормальная производная от перемещения границы мембраны в любой момент времени, а именно
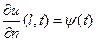 (55)
(55)
Как мы помним, производная по нормали с точностью до постоянного множителя T соответствует напряжению, поэтому говорят, что условие (55) задает напряжение на границе мембраны. По третьему закону Ньютона это напряжение равно вертикальной составляющей внешней силы, приходящейся на единицу длины граничного контура. В случае, если на границу не действует никаких сил, условие (55) становится однородным.
Граничное условие третьего рода задает в любой момент времени сумму перемещения границы и напряжения с некоторым постоянным множителем h:
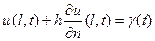 (56)
(56)
Если γ (t) равно нулю, условие (56) становится однородным и в этом случае имеет простую физическую интерпретацию. Для этого нужно представить, что граница мембраны скреплена упругим образом с плоскостью (x, y), как это показано на Рис.3.2.
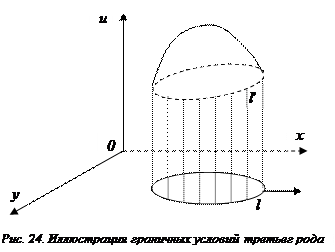
Тогда вертикальная составляющая напряжения на границе мембраны будет равна внешней упругой силе, приходящейся на единицу длины граничного контура, которая в каждой точке по закону Гука пропорциональна смещению в этой точке и направлена в сторону противоположную смещению (как и проекция T на ось u), т.е. равна 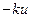 . Следовательно, можно записать, что
. Следовательно, можно записать, что
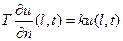
или
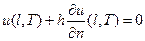 , (57)
, (57)
где 
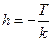 .
.
Теперь можно представить, что основание упругого закрепления границы перемещается параллельно оси u по закону ξ (t). Тогда сила, развиваемая упругим закреплением, будет равна – k [ u – ξ (t)], и мы можем записать
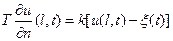
Разделив все члены этого равенства на k и обозначив 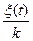 через γ (t), мы и получим формулу (56).
через γ (t), мы и получим формулу (56).




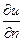 , где n – внешняя нормаль к контуру l.
, где n – внешняя нормаль к контуру l.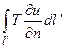
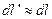 , то мы можем в записанном интеграле путь интегрирования dl 'заменить на dl. Тогда применяя формулу Грина, получим
, то мы можем в записанном интеграле путь интегрирования dl 'заменить на dl. Тогда применяя формулу Грина, получим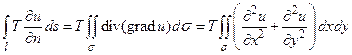 (46)
(46)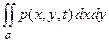 (47)
(47)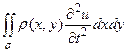 (48)
(48)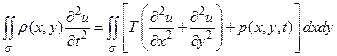 ,
,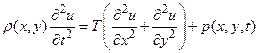 (49)
(49)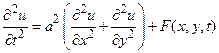 , (50)
, (50)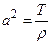 и
и 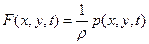
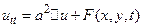 (51)
(51)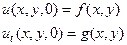 (52)
(52)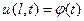 (53)
(53)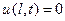 (54))
(54))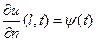 (55)
(55)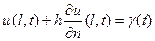 (56)
(56)
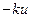 . Следовательно, можно записать, что
. Следовательно, можно записать, что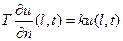
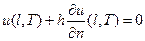 , (57)
, (57)
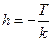 .
.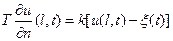
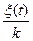 через γ (t), мы и получим формулу (56).
через γ (t), мы и получим формулу (56).


