1.Знать определения оригинала и изображения. Изображения некоторых функций.
2.Используя таблицу основных формул соответствия и теоремы операционного исчисления, уметь находить изображения оригиналов и оригиналы по их изображениям.
3.Уметь находить изображения дифференциального выражения.
4.Уметь находить операционным методом частные решения дифференциальных уравнений с постоянными коэффициентами.
Задания для самостоятельного выполнения
1 Найти изображение F (p) по заданному оригиналу f (t):
а) 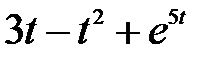 ; б)
; б) 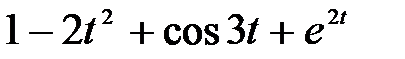 ; в)
; в) 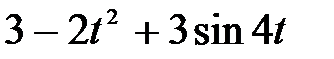 .
.
2 Найти оригинал f (t) по изображению F (p):
а) 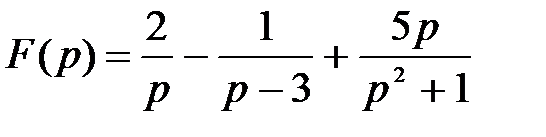 ; б)
; б) 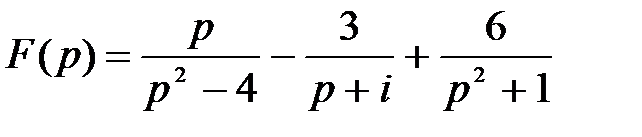 ;
;
в) 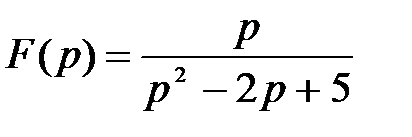 .
.
3 Найти изображение дифференциального выражения:
а) 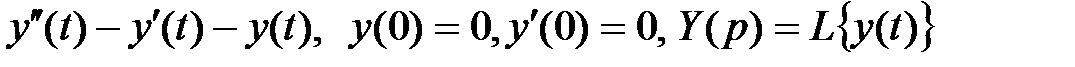 ;
;
б)  ;
;
в) 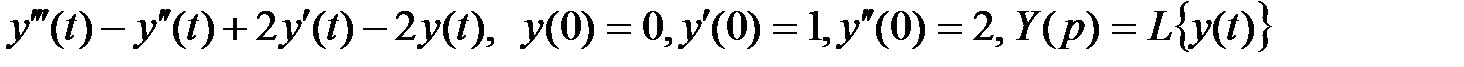 .
.
4 Операционным методом найти решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
а) 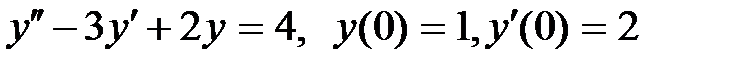 ; б)
; б) 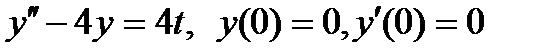 .
.
Образцы решения заданий
Любая комплексная функция f (t) действительного переменного t называется оригиналом, если она удовлетворяет следующим условиям:
1) f (t) – кусочно–непрерывная при t ≥ 0, это значит, что она либо непрерывна, либо в каждом конечном интервале имеет лишь конечное число точек разрыва 1-го рода;
2) f (t) ≡ 0 при t < 0;
3) при t → ∞ функция f (t) растёт не быстрее некоторой показательной функции (имеет ограниченную степень роста), т.е. существует такое положительное число М и такое неотрицательное число s, что для всех t ≥ 0 выполняется неравенство:| f (t) | ≤ M ∙ est, М > 0, s ≥ 0.
Точная нижняя грань s 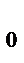
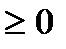 тех значений s, для которых выполняется указанное условие, называется показателем ро ста функции f (t).
тех значений s, для которых выполняется указанное условие, называется показателем ро ста функции f (t).
Изображением функции f (t) по Лапласу называется функция F (p) комплексного переменного p=s+i  из некоторой области D плоскости комплексного переменного p, определяемая равенством
из некоторой области D плоскости комплексного переменного p, определяемая равенством
F (p) = 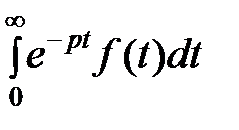 .
.
Связь между функциями f (t)и F (p) будем обозначать в дальнейшем следующим образом: f (t) = L –1{ F (p)} или F (p) = L { f (t)}.
Первую запись следует читать так: «Оригинал f (t) имеет изображение F (p)». Вторую запись следует читать так: «Изображение F (p) имеет оригинал f (t)» или «f (t) является оригиналом изображения F (p)». Используются также и другие обозначения.
Свойства преобразования Лапласа
1 Теорема единственности. Если два изображения F (р) и Φ (р) совпадают, то совпадают между собой и соответствующие им оригиналы во всех точках, за исключением, быть может, точек разрыва. То есть, если
F (p) = L { f (t)}, Ф (p) = L {φ (t)} и F (p) ≡ Ф (p), то f (t) ≡ φ (t)
во всех точках непрерывности f (t).
2 Теорема линейности. Если f (t) = L –1{ F (p)}, g (t) = L –1{ G (p)} для любых действительных или комплексных постоянных с 1 и с 2
с 1 f (t) + с 2 g (t) = с 1 L –1{ F (p)} + с 2 L –1{ G (p)}, Re p > s 0( k ) (k = 1,2,)
т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
3. Теорема подобия. Если f (t) = L –1{ F (p)}, Re p > s 0, то для любого числа а > 0
f (аt) = 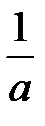 L –1{
L –1{ 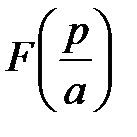 }, Re p > аs 0,
}, Re p > аs 0,
т.е. умножение аргумента оригинала на положительное число приводит к делению аргумента изображения и самого изображения на то же число а.
4. Теорема запаздывания. Если f (t) = L –1{ F (p)}, Re p > s 0, то для любого положительного числа τ
f (t – τ) = e– рτ L –1{ F (p)}, Re p > s 0.
5. Теорема о смещении изображения (затухания). Если
f (t) = L –1{ F (p)}, Re p > s 0, то для любого действительного или комплексного числа α
eαtf (t) = L –1{ F (р – α)}, Re (р – α) > s 0,
т.е. умножение оригинала на функцию eαt, влечёт за собой «смещение» переменной p.
6. Теорема дифференцирования оригинала. Если функции f(t), f  (t), …, f
(t), …, f 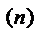 (t) являются функциями-оригиналами, то
(t) являются функциями-оригиналами, то
f / (t) = p L –1{ F (p)} – f (0),
f // (t) = p 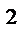 L –1{ F (p)} -p f ( 0) – f / (0),
L –1{ F (p)} -p f ( 0) – f / (0),
…
f 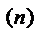 (t) = p
(t) = p 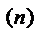 L –1{ F (p)} – p
L –1{ F (p)} – p 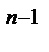 f (0) – p
f (0) – p 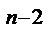 f / (0) -…-f
f / (0) -…-f 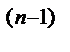 (0).
(0).
Величина f 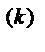 (0), k= 0, 1, …, n-1, понимается как
(0), k= 0, 1, …, n-1, понимается как 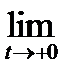 f
f 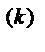 (t).
(t).
7. Теорема об интегрировании оригинала. Если функция f (t) является оригиналом и f (t) = L –1{ F (p)} то функция g (t) = 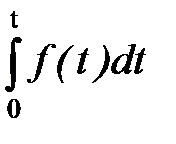 также является оригиналом и g (t) =
также является оригиналом и g (t) = 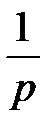 L –1{ F (p)}
L –1{ F (p)}
т.е. интегрирование оригинала в пределах от 0 до t приводит к делению изображения на p.
На основании определений оригинала и изображения и основных свойств преобразований Лапласа можно составить таблицу основных формул соответствия (таблица 6. 1).
Таблица 6. 1 – Таблица основных формул соответствия
| Номер
формулы
| Оригинал
| Изображение
|
|
|
| 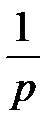
|
|
|
eαt
| 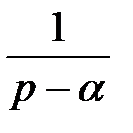
|
|
|
sin ω t
|   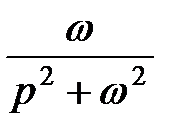 
|
|
|
cos ω t
| 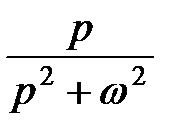
|
|
|
sh ω t
| 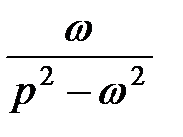
|
|
|
ch ω t
| 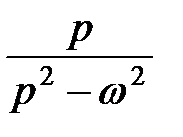
|
|
|
t
| 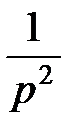
|
|
|
tn
| 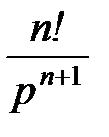
|
|
|
tn ∙ eαt
| 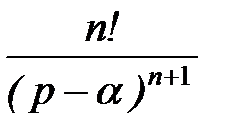
|
|
|
t ∙ sin ω t
| 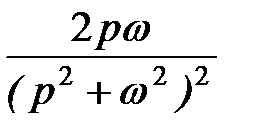
|
|
|
t ∙ cos ω t
| 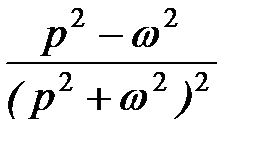
|
Задание 1. Найти изображение функции 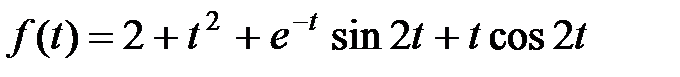 , используя основные свойства (теоремы) преобразования Лапласа.
, используя основные свойства (теоремы) преобразования Лапласа.
Решение. Найдем изображение каждого из слагаемых функции 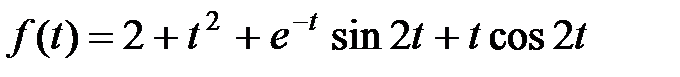 . Из таблиц соответствия известно, что:
. Из таблиц соответствия известно, что:
1 = L –1{ 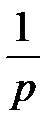 }.
}.
По теореме об интегрировании оригинала имеем
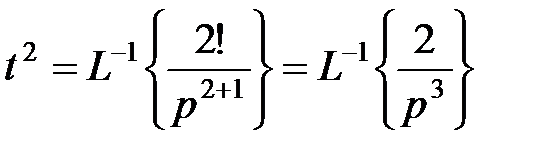 .
.
Так как 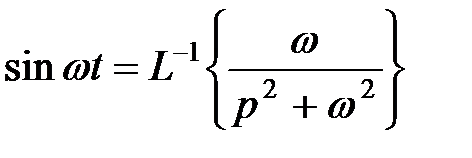 , то
, то 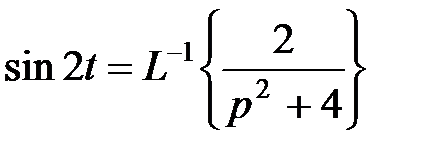 . Тогда по теореме о смещении изображения (затухания) получим
. Тогда по теореме о смещении изображения (затухания) получим
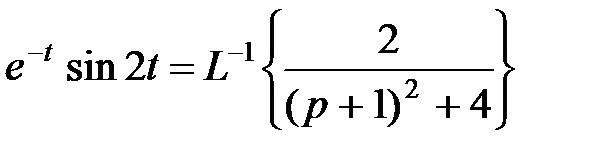 .
.
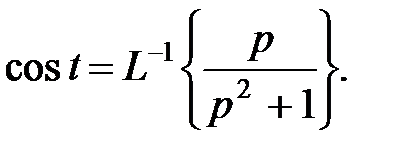
Применяя теорему подобия, находим
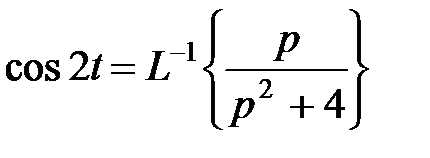 .
.
Для нахождения изображения функции 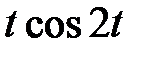 применим теорему о дифференцировании изображения. Получим
применим теорему о дифференцировании изображения. Получим
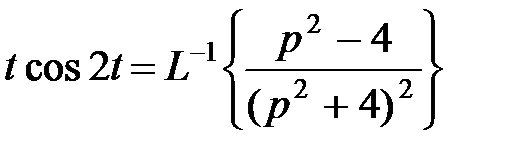 .
.
Далее, применяя теорему линейности преобразования Лапласа, получим

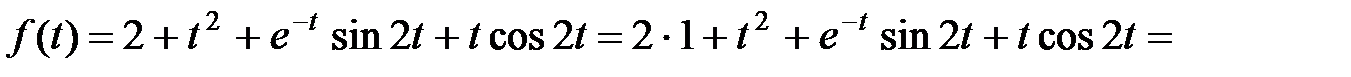
= 2 L –1{ 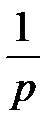 } +
} + 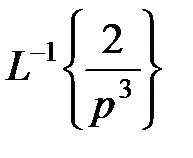 +
+ 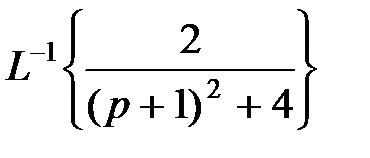 +
+ 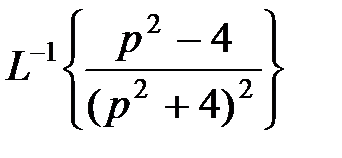 .
.
Следовательно,
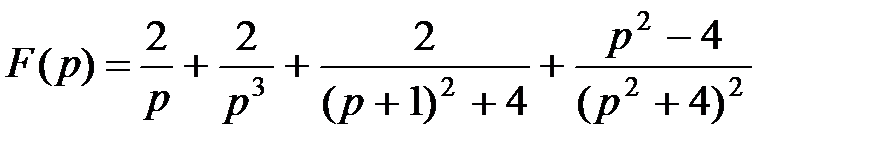 .
.
Задание 2. Найти оригинал f (t) по изображению 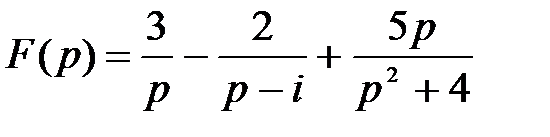 .
.
Решение. Используя табличные операционные соотношения и свойства линейности, получаем 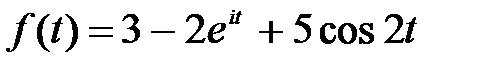 .
.
Задание 3. Найти изображение дифференциального выражения 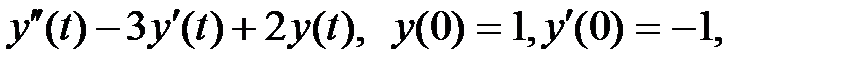 y (t) = L –1{ Y (p)}
y (t) = L –1{ Y (p)}
Решение. На основании свойства дифференцирования оригинала получаем:
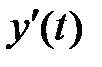 = p L –1{ Y (p)} – y (0),
= p L –1{ Y (p)} – y (0),
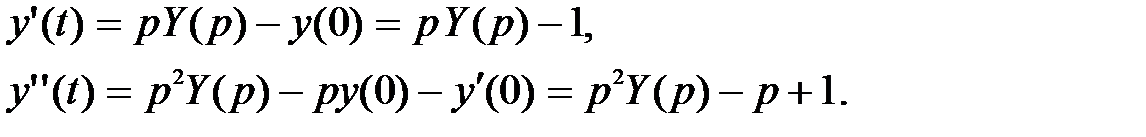
Используя свойство линейности, находим
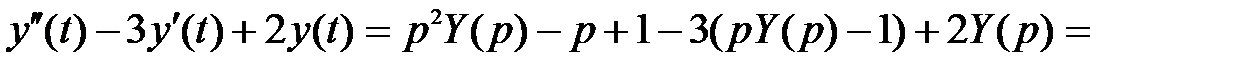
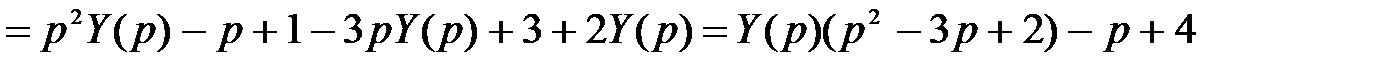 ,
,



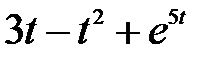 ; б)
; б) 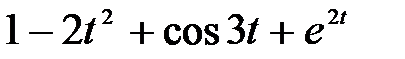 ; в)
; в) 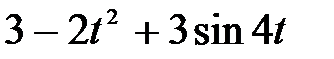 .
.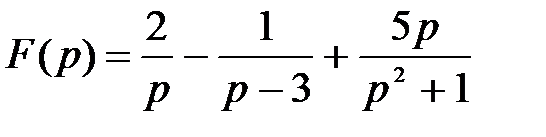 ; б)
; б) 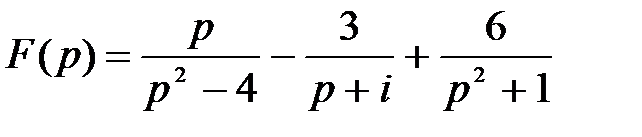 ;
;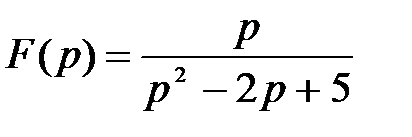 .
.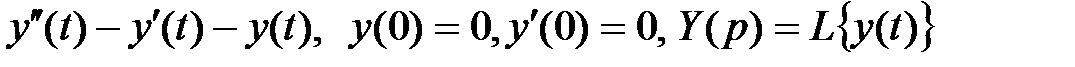 ;
; ;
;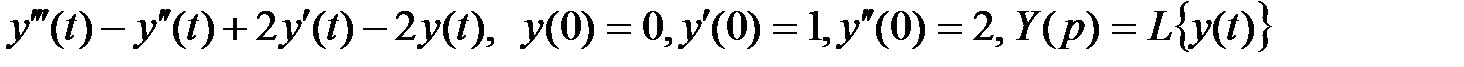 .
.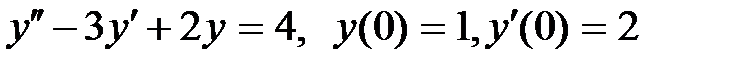 ; б)
; б) 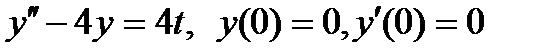 .
.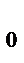
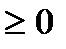 тех значений s, для которых выполняется указанное условие, называется показателем ро ста функции f (t).
тех значений s, для которых выполняется указанное условие, называется показателем ро ста функции f (t). из некоторой области D плоскости комплексного переменного p, определяемая равенством
из некоторой области D плоскости комплексного переменного p, определяемая равенством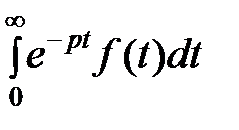 .
.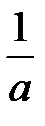 L –1{
L –1{ 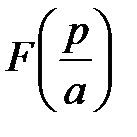 }, Re p > аs 0,
}, Re p > аs 0, (t), …, f
(t), …, f 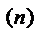 (t) являются функциями-оригиналами, то
(t) являются функциями-оригиналами, то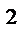 L –1{ F (p)} -p f ( 0) – f / (0),
L –1{ F (p)} -p f ( 0) – f / (0),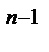 f (0) – p
f (0) – p 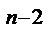 f / (0) -…-f
f / (0) -…-f 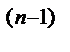 (0).
(0).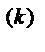 (0), k= 0, 1, …, n-1, понимается как
(0), k= 0, 1, …, n-1, понимается как 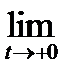 f
f 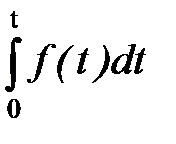 также является оригиналом и g (t) =
также является оригиналом и g (t) = 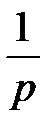 L –1{ F (p)}
L –1{ F (p)}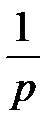
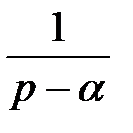

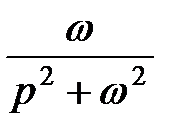
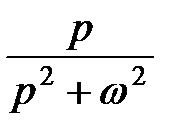
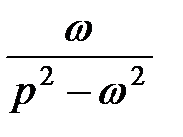
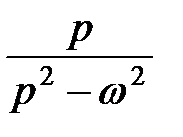
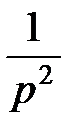
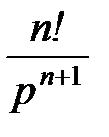
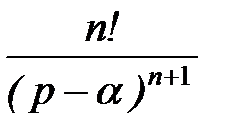
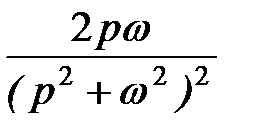
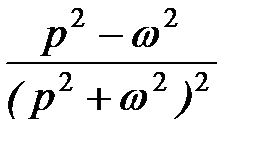
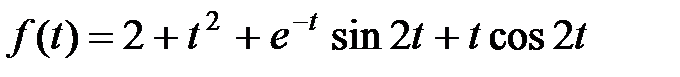 , используя основные свойства (теоремы) преобразования Лапласа.
, используя основные свойства (теоремы) преобразования Лапласа.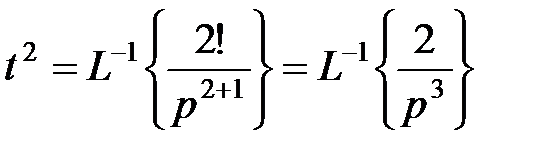 .
.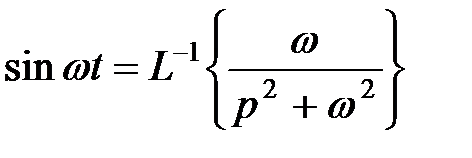 , то
, то 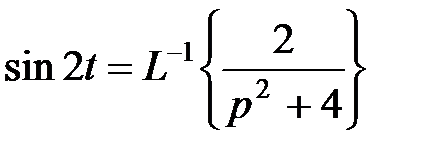 . Тогда по теореме о смещении изображения (затухания) получим
. Тогда по теореме о смещении изображения (затухания) получим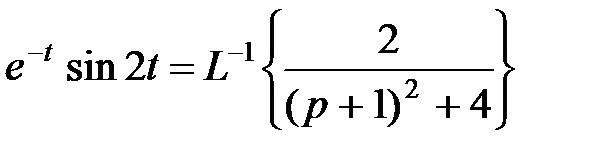 .
.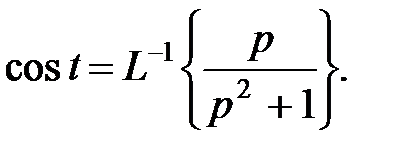
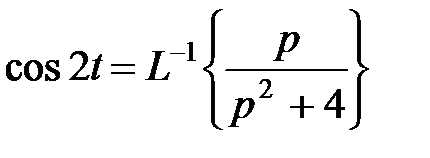 .
.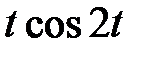 применим теорему о дифференцировании изображения. Получим
применим теорему о дифференцировании изображения. Получим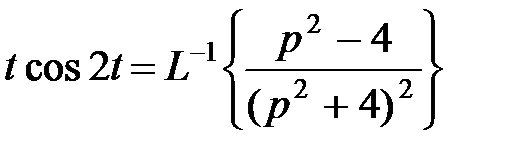 .
.
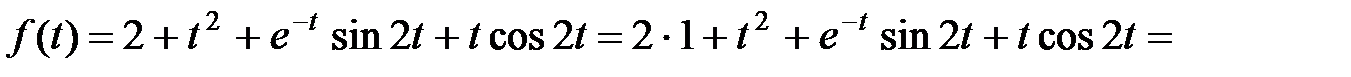
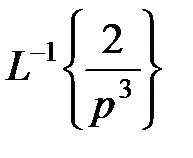 +
+ 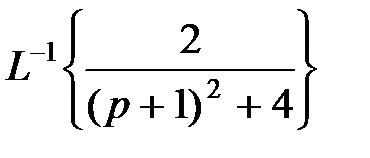 +
+ 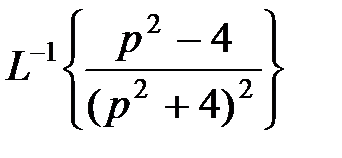 .
.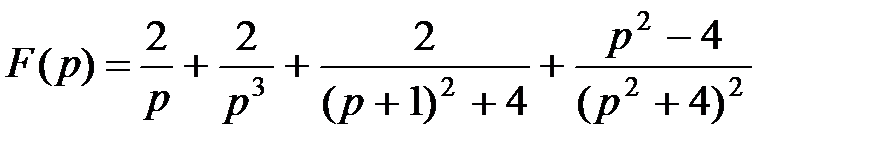 .
.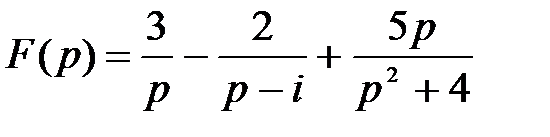 .
.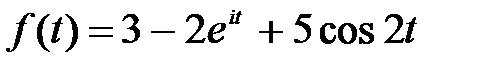 .
.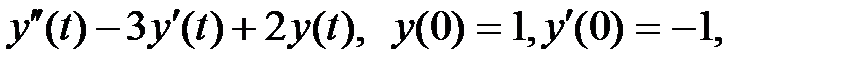 y (t) = L –1{ Y (p)}
y (t) = L –1{ Y (p)}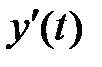 = p L –1{ Y (p)} – y (0),
= p L –1{ Y (p)} – y (0),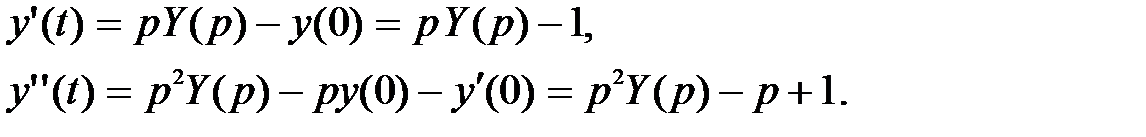
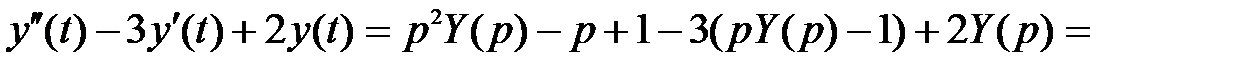
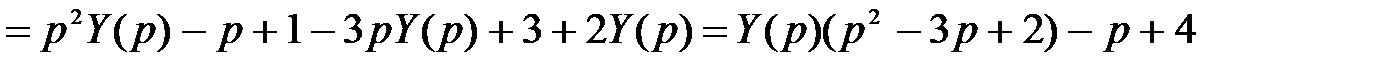 ,
,


