Дифференциальных уравнений с постоянными коэффициентами и
Непрерывной правой частью
Рассмотрим линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
 , (6. 1)
, (6. 1)
f (t) – непрерывная функция действительного переменного.
Требуется найти частное решение уравнения, удовлетворяющее начальным условиям:
 (6. 2)
(6. 2)
где  – заданные числа (задача Коши).
– заданные числа (задача Коши).
Будем предполагать, что функция f (t) является оригиналом. Искомую функцию y (t) и её производные  также предполагаем оригиналами. Полагаем f (t) = L –1{ F (p)}, y (t) = L –1{ Y (p)}.
также предполагаем оригиналами. Полагаем f (t) = L –1{ F (p)}, y (t) = L –1{ Y (p)}.
Для решения поставленной задачи (6. 1), (6. 2) перейдём от уравнения (6. 1) к изображающему (или операторному) уравнению, связывающему изображения Y (p) и F (p).
Применяя два раз теорему о дифференцировании оригинала, получим:
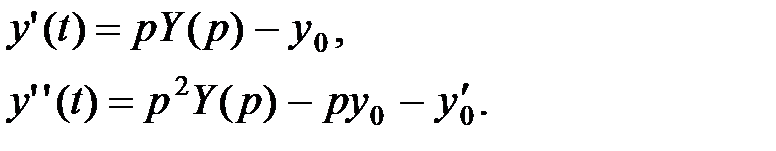
Далее, применяя теорему линейности перейдём от уравнения (6. 1) к операторному уравнению:
 . (6.3)
. (6.3)
Из уравнения (6. 3) выразим 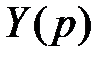 .Искомое частное решение y (t) является оригиналом, соответствующим данному изображению. Оно определяется с помощью таблиц соответствия.
.Искомое частное решение y (t) является оригиналом, соответствующим данному изображению. Оно определяется с помощью таблиц соответствия.
Задание 4. Найти частное решение уравнения  удовлетворяющее начальным условиям:
удовлетворяющее начальным условиям: 
Решение. Обозначим через y (t) искомое частное решение, через Y (p) – его изображение. Тогда:
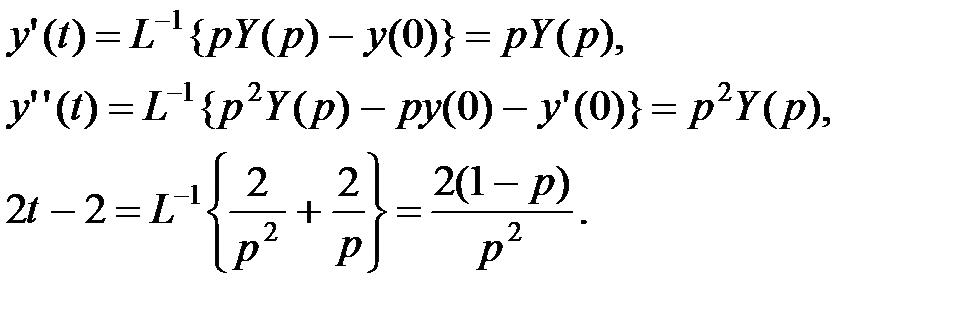
Операторное уравнение будет иметь вид

откуда
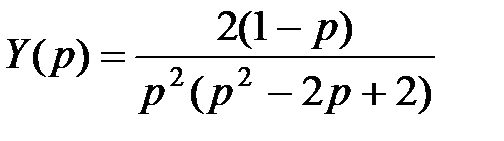 .
.
Дробь  разложим на сумму простых элементарных дробей и найдем коэффициенты разложения:
разложим на сумму простых элементарных дробей и найдем коэффициенты разложения:


Из системы:

Откуда 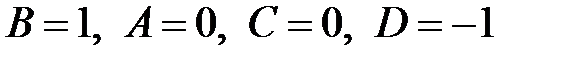 .
.
Тогда

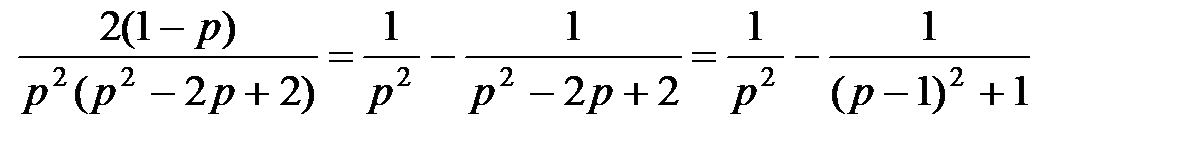 .
.
Используя таблицы соответствия, найдём: 
Таким образом, искомое частное решение: 
Тема 7. Основные уравнения математической физики.
1.Знать определение дифференциального уравнения в частных производных.
2.Знать, что является решением дифференциальных уравнений в частных производных, какие условия являются начальными, а какие граничными (краевыми).
3.Уметь находить решение задачи Коши о колебаниях бесконечной струны.
Задания для самостоятельного выполнения
1 Методом Даламбера найти уравнение u = u (x. t) формы однородной бесконечной струны, определяемой волновым уравнением

если в начальный момент t 0 = 0 форма струны и скорость точки струны с абсциссой х определяются соответственно заданными функциями
u(x,0) = fx), 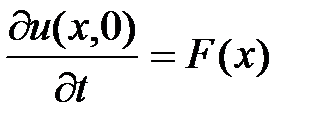 :
:
а)  ; б)
; б)  .
.
Образец решения задания
Рассмотрим задачу Коши для бесконечной однородной струны. Пусть требуется найти решение волнового уравнения

при начальных условиях
u(x,0) = fx),  .
.
Искомое решение задачи Коши для бесконечной струны u (x,t) определяется по формуле:
 ,
,
которая называется формулой Даламбера для бесконечной струны.
Задание 1. Найти форму бесконечной однородной струны, если начальная форма струны f (x) = ex, а начальная скорость ее F (x) = cos2 x.
Решение. Искомое решение u (x,t) найдем по формуле Даламбера:
 .
.
Так как f (x) = ex, F (x) = cos2 x, то

 .
.
Тема 8. Математическая статистика



 , (6. 1)
, (6. 1) (6. 2)
(6. 2) – заданные числа (задача Коши).
– заданные числа (задача Коши). также предполагаем оригиналами. Полагаем f (t) = L –1{ F (p)}, y (t) = L –1{ Y (p)}.
также предполагаем оригиналами. Полагаем f (t) = L –1{ F (p)}, y (t) = L –1{ Y (p)}.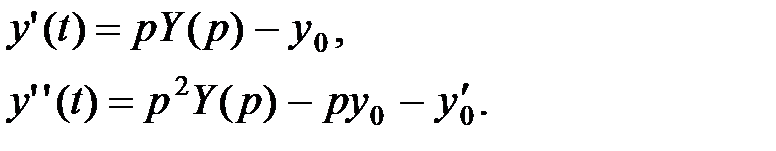
 . (6.3)
. (6.3)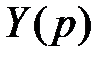 .Искомое частное решение y (t) является оригиналом, соответствующим данному изображению. Оно определяется с помощью таблиц соответствия.
.Искомое частное решение y (t) является оригиналом, соответствующим данному изображению. Оно определяется с помощью таблиц соответствия. удовлетворяющее начальным условиям:
удовлетворяющее начальным условиям: 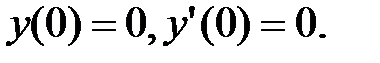
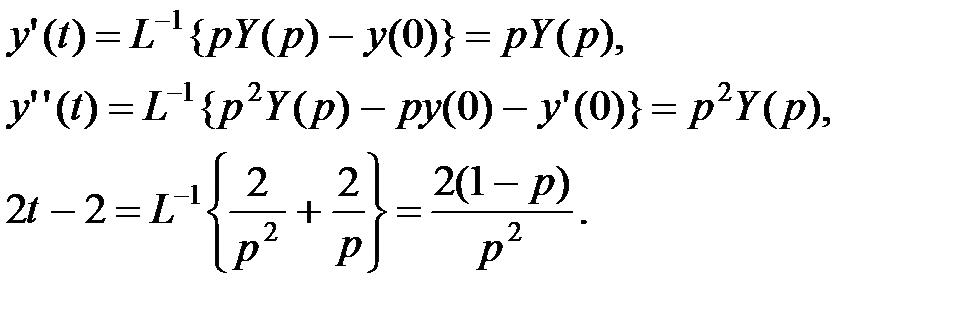

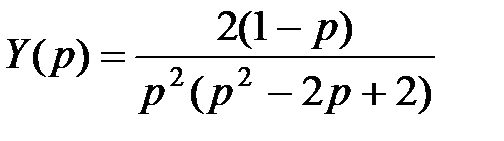 .
. разложим на сумму простых элементарных дробей и найдем коэффициенты разложения:
разложим на сумму простых элементарных дробей и найдем коэффициенты разложения:


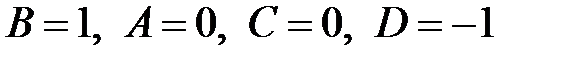 .
.
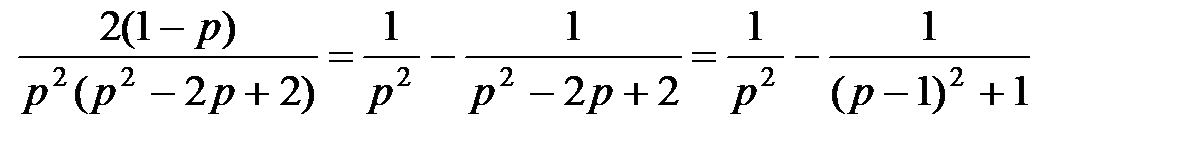 .
.


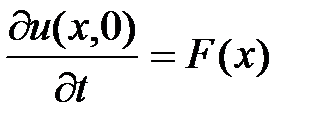 :
: ; б)
; б)  .
.
 .
. ,
, .
.
 .
.


