Чтобы построить ряд Фурье функции  заданной на отрезке
заданной на отрезке  , кусочно-непрерывной на
, кусочно-непрерывной на 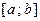 , имеющей в каждой точке
, имеющей в каждой точке  конечные односторонние производные, воспользуемся следующей с х е м о й:
конечные односторонние производные, воспользуемся следующей с х е м о й:
· Построим функцию  , называемую
, называемую  периодическим продолжением функции
периодическим продолжением функции  на всю числовую ось, совпадающую с функцией
на всю числовую ось, совпадающую с функцией  на
на 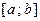 и удовлетворяющую условиям теоремы Дирихле – Дини. Число
и удовлетворяющую условиям теоремы Дирихле – Дини. Число  любое число, удовлетворяющее неравенству:
любое число, удовлетворяющее неравенству:  .
.
· Разложим функцию  в ряд Фурье. Этот ряд сходится в любой точке
в ряд Фурье. Этот ряд сходится в любой точке  и его сумма вычисляется по формуле:
и его сумма вычисляется по формуле:

· Назовем построенный ряд рядом Фурье функции  на отрезке
на отрезке  . Он сходится и имеет своей суммой число
. Он сходится и имеет своей суммой число  в любой точке
в любой точке  где функция
где функция  непрерывна.
непрерывна.
З а м е ч а н и е 13. Разлагая в ряд Фурье непериодическую функцию  заданную на отрезке
заданную на отрезке 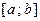 , мы имеем возможность по собственному усмотрению, во-первых, варъировать числом
, мы имеем возможность по собственному усмотрению, во-первых, варъировать числом  (выбирая его из условия
(выбирая его из условия  во-вторых, доопределять функцию
во-вторых, доопределять функцию  на всю числовую ось различными способами. Это приводит к различным (по внешнему виду) рядам Фурье для функции
на всю числовую ось различными способами. Это приводит к различным (по внешнему виду) рядам Фурье для функции  на
на 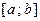 , имеющим в любой точке
, имеющим в любой точке 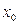 непрерывности функции
непрерывности функции  одну и ту же сумму
одну и ту же сумму  .
.
З а м е ч а н и е 14. Любую функцию  определенную на отрезке
определенную на отрезке  и обладающую там указанными в теореме Дирихле – Дини свойствами непрерывности, можно на этом отрезке разложить как в ряд Фурье вида (17), вида (19), так и общего вида (14). Это объясняется возможностью продления функции
и обладающую там указанными в теореме Дирихле – Дини свойствами непрерывности, можно на этом отрезке разложить как в ряд Фурье вида (17), вида (19), так и общего вида (14). Это объясняется возможностью продления функции  на
на  или по закону четности, или нечетности, или какому–либо другому.
или по закону четности, или нечетности, или какому–либо другому.
З а м е ч а н и е 15. Для решения примеров полезно знание следующих формул, легко получаемых методом интегрирования по частям:
 (22)
(22)
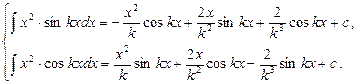 (23)
(23)
З а м е ч а н и е 16. Ряд Фурье (14) функции  можно почленно интегрировать в интервале
можно почленно интегрировать в интервале  получая разложение в ряд Фурье функции
получая разложение в ряд Фурье функции 
ПРИМЕРЫ С РЕШЕНИЯМИ
П р и м е р 1. Найти ряд Фурье  периодической функции
периодической функции  которая задается на отрезке
которая задается на отрезке  равенством
равенством 
Р е ш е н и е. График функции  изображен на рис. 1.
изображен на рис. 1.
 у
у
p
- 3 p -2 p -p О p 2 p 3 p х
Рис. 1
Эта функция непрерывна в любой точке  и кусочно непрерывно-дифференцируема, так как
и кусочно непрерывно-дифференцируема, так как  имеет в точках
имеет в точках  разрыв первого рода, а в остальных точках – непрерывна.
разрыв первого рода, а в остальных точках – непрерывна.
Следовательно, условия теоремы Дирихле – Дини выполнены при  и рассматриваемую функцию можно разложить в ряд Фурье (14), сходящийся в любой точке
и рассматриваемую функцию можно разложить в ряд Фурье (14), сходящийся в любой точке  к числу
к числу 
Учитывая четность функции  ее коэффициенты Фурье вычисляем по формуле (18):
ее коэффициенты Фурье вычисляем по формуле (18):




Тогда по формуле (17) находим:

О т в е т: 
П р и м е р 2. Разложить в ряд Фурье функцию:
 при
при 
Р е ш е н и е. Рассмотрим вспомогательную  – периодическую функцию
– периодическую функцию  определенную на
определенную на  и совпадающую с
и совпадающую с  на
на  (рис. 2).
(рис. 2).
 у
у
p
- 3 p -2 p -p О p 2 p 3 p х
-p 
Рис. 2
Функция  является
является  периодической, кусочно–непрерывной и кусочно непрерывно-дифференцируемой. Причем функции
периодической, кусочно–непрерывной и кусочно непрерывно-дифференцируемой. Причем функции  и
и  терпят разрывы первого рода в точках вида
терпят разрывы первого рода в точках вида 
Следовательно, ряд Фурье, составленный для функции  совпадет при
совпадет при  с функцией
с функцией 
Поэтому, учитывая нечетность функции  и формулы (20) при
и формулы (20) при  получаем:
получаем:


Значит, по формуле (19) находим искомое разложение:

О т в е т: 
П р и м е р 3. На интервале  разложить в ряд Фурье функцию:
разложить в ряд Фурье функцию:

Р е ш е н и е. График функции  изображен на рис. 3.
изображен на рис. 3.
 у
у
p

 -p О p х
-p О p х
 - 1
- 1
Рис. 3
Рассмотрим вспомогательную  периодическую функцию
периодическую функцию  график которой изображен на рис. 4.
график которой изображен на рис. 4.
 у
у
p
- 3 p -2 p -p О p 2 p 3 p х
- 1 Рис. 4
Непосредственно проверяется, что функция  удовлетворяет условиям теоремы Дирихле – Дини. По формулам (15) – (16), где
удовлетворяет условиям теоремы Дирихле – Дини. По формулам (15) – (16), где  найдем коэффициенты ряда Фурье функции
найдем коэффициенты ряда Фурье функции 

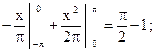











Следовательно, по формуле (14) получаем:
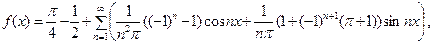
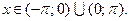
Заметим, что при  построенный ряд имеет своей суммой число:
построенный ряд имеет своей суммой число:

При  сумма данного ряда равна числу:
сумма данного ряда равна числу:

О т в е т:  ,
, 
П р и м е р 4. Для функции  из примера 1 найти сумму
из примера 1 найти сумму  ее ряда Фурье.
ее ряда Фурье.
Р е ш е н и е. Функция  , рассматриваемая в примере 1 (ее график см. на рис.1), удовлетворяет всем условиям Дирихле – Дини:
, рассматриваемая в примере 1 (ее график см. на рис.1), удовлетворяет всем условиям Дирихле – Дини:  периодическая, непрерывная на всей вещественной оси, дифференцируемая во всех точках
периодическая, непрерывная на всей вещественной оси, дифференцируемая во всех точках  в точках вида
в точках вида 
 имеет конечные односторонние производные:
имеет конечные односторонние производные:

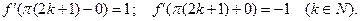
Поэтому, используя формулу (21), заключаем: 
О т в е т: 
П р и м е р 5. Для функции  из примера 2 найти сумму ее ряда Фурье.
из примера 2 найти сумму ее ряда Фурье.
Р е ш е н и е. В данном случае функция  является
является  периодической, непрерывной во всех точках вещественной оси, кроме точек
периодической, непрерывной во всех точках вещественной оси, кроме точек  терпит разрыв первого рода в любой из точек вида
терпит разрыв первого рода в любой из точек вида  дифференцируемая во всех точках
дифференцируемая во всех точках 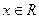 , включая точки разрыва функции
, включая точки разрыва функции  . Следовательно, по формуле (21) находим:
. Следовательно, по формуле (21) находим:
 если
если 
 ;
;
 если
если 
О т в е т:  если
если 
 если
если 
П р и м е р 6. Найти сумму ряда Фурье функции  периода
периода  если
если

Р е ш е н и е. Графики функции  и ее периодического продолжения приведены на рис. 5.
и ее периодического продолжения приведены на рис. 5.
 у
у

 1
1

- 3 - 1 О 1 3 х
Рис. 5
а) Найдем коэффициенты Фурье функции  Учитывая, что
Учитывая, что  то есть
то есть  вычисляем:
вычисляем:

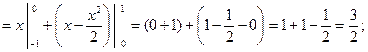




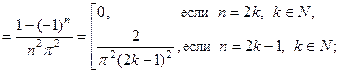






Итак, получили разложение:
 (24)
(24)
б) Проверим выполнение условий теоремы Дирихле – Дини:
- функция  является периодической с периодом
является периодической с периодом 
- функция  является непрерывной во всех точках вещественной оси, кроме
является непрерывной во всех точках вещественной оси, кроме  терпит разрыв первого рода в точках вида
терпит разрыв первого рода в точках вида 
- функция  имеет производную во всех точках, кроме
имеет производную во всех точках, кроме  В точках
В точках  она имеет конечные односторонние производные:
она имеет конечные односторонние производные:


Следовательно, по теореме Дирихле – Дини заключаем: ряд Фурье (24) сходится в любой точке 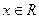 и имеет своей суммой функцию
и имеет своей суммой функцию  вида:
вида:
 при
при 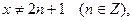

График функции  изображен на рис. 6.
изображен на рис. 6.
 у
у


 1
1














- 3 - 1 О 1 3 х Рис. 6
О т в е т:  при
при 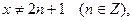

П р и м е р 7. Разложить в ряд Фурье функцию  при
при 
Р е ш е н и е. На рис. 7 представлен график функции  с ее продолжением периода
с ее продолжением периода 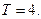
 у
у
 3
3

 -7 -3 О 1 5 9 х
-7 -3 О 1 5 9 х
 -1 Рис. 7
-1 Рис. 7
Для построенной таким образом периодической функции  выполнены условия теоремы Дирихле – Дини. Воспользовавшись замечанием 6, где
выполнены условия теоремы Дирихле – Дини. Воспользовавшись замечанием 6, где 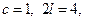 находим коэффициенты Фурье функции
находим коэффициенты Фурье функции 


 =
= 







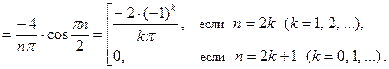
О т в е т: 

П р и м е р 8. Разложить в ряд Фурье функцию

Р е ш е н и е. График функции  изображен на рис. 8.
изображен на рис. 8.
 у
у

 3
3

 1
1
-2 О 2 х Рис. 8
Рассмотрим функцию  (см. рис. 9), являющуюся для
(см. рис. 9), являющуюся для  ее
ее  периодическим продолжением, где
периодическим продолжением, где 
 у
у

-6 -4 -2 О 2 4 6 х Рис. 9
Нетрудно видеть, что функция  удовлетворяет условиям теоремы Дирихле – Дини:
удовлетворяет условиям теоремы Дирихле – Дини:  периодическая; кусочно–непрерывная; имеет разрыв первого рода в точках вида
периодическая; кусочно–непрерывная; имеет разрыв первого рода в точках вида  имеет непрерывную производную
имеет непрерывную производную  во всех точках
во всех точках 
Построим ряд Фурье для функции  Найдем предварительно его коэффициенты:
Найдем предварительно его коэффициенты:









Следовательно, получаем:
 (25)
(25)
Ряд (25) сходится и имеет сумму:  при
при 
 при
при 
 при
при 
Следовательно, справедливо равенство:
 при
при 
О т в е т:  .
.
П р и м е р 9. Функцию  , заданную на интервале
, заданную на интервале  , разложить в ряд Фурье по синусам.
, разложить в ряд Фурье по синусам.
Р е ш е н и е. Рассмотрим вспомогательную функцию  график которой изображен на рис. 10.
график которой изображен на рис. 10.
 у
у
p
 -p О p 2p 3p х
-p О p 2p 3p х


 - p
- p
Рис. 10
Она  периодическая, нечетная. По формуле (20) вычисляем:
периодическая, нечетная. По формуле (20) вычисляем:




Следовательно, согласно теореме Дирихле – Дини получаем:

О т в е т: 
П р и м е р 10. Функцию  на отрезке
на отрезке  разложить в ряд Фурье по косинусам.
разложить в ряд Фурье по косинусам.
Р е ш е н и е. Рассмотрим  периодическую
периодическую  четную функцию
четную функцию  график которой изображен на рис.11.
график которой изображен на рис.11.
 у
у
2







4 - 2О24 х Рис. 11
Для нее по формулам (18) находим коэффициенты ряда Фурье:





Следовательно, учитывая теорему Дирихле – Дини, получаем:

О т в е т: 

П р и м е р 11. Разложить в ряд Фурье функцию 
а) на  по синусам; б) на
по синусам; б) на  по косинусам; в) на
по косинусам; в) на 
Р е ш е н и е. а) Чтобы разложить функцию  на
на  только по синусам, рассмотрим ее нечетное
только по синусам, рассмотрим ее нечетное  периодическое продолжение на всю числовую ось (см. рис. 12).
периодическое продолжение на всю числовую ось (см. рис. 12).
 у
у
 2p2
2p2


-3p -p О p 3p х
-2p2 Рис. 12
Найдем для этой функции коэффициенты Фурье:


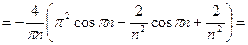

Следовательно, при 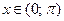 справедливо равенство:
справедливо равенство:

б) Чтобы разложить функцию  на
на  только по косинусам, рассмотрим ее четное
только по косинусам, рассмотрим ее четное  периодическое продолжение на всю числовую ось (см. рис. 13).
периодическое продолжение на всю числовую ось (см. рис. 13).
 у
у





 2p2
2p2

-3p -p О p 3p х Рис. 13
Найдем для этой функции коэффициенты Фурье:





Следовательно, при 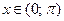 для функции
для функции  справедливо равенство:
справедливо равенство: 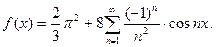
в) Для того чтобы функцию  разложить на интервале
разложить на интервале 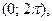 рассмотрим ее
рассмотрим ее  периодическое продолжение на всю числовую ось, график которого приведен на рис. 14.
периодическое продолжение на всю числовую ось, график которого приведен на рис. 14.
 у
у
8p2

 -4p -2p О 2p 4p х Рис. 14
-4p -2p О 2p 4p х Рис. 14
Вычислим для этой функции коэффициенты Фурье:








Следовательно, на  для функции
для функции  справедливо представление:
справедливо представление: 
О т в е т: а)  б)
б) 
в) 
П р и м е р 12. Пользуясь разложением функции  в ряд Фурье на
в ряд Фурье на  , найти сумму ряда: а)
, найти сумму ряда: а)  б)
б) 
Р е ш е н и е. Функция  , заданная на отрезке
, заданная на отрезке  и продолженная четным образом, имеет ряд Фурье:
и продолженная четным образом, имеет ряд Фурье:
 (26)
(26)
Следовательно, при  из (26) находим:
из (26) находим:

При  формула (26) принимает вид:
формула (26) принимает вид:

О т в е т: а)  б)
б) 
ПРИМЕРЫ
Разложить в ряд Фурье функции:
1. 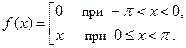 2.
2. 
3.  а) по косинусам, б) по синусам.
а) по косинусам, б) по синусам.
4.  по косинусам. 5.
по косинусам. 5.  на
на  по синусам.
по синусам.
6.  на
на  7.
7.  на
на 
8.  на
на 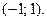 9.
9.  на
на 
10.  и
и  на интервале
на интервале  . Указание: воспользоваться разложением
. Указание: воспользоваться разложением  и почленным интегрированием.
и почленным интегрированием.
♦ ♦ ♦
Разложить в ряд Фурье функции:
11.  12.
12. 
13.  14.
14. 
15.  на
на 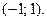 16.
16.  на
на 
17.  по косинусам. 18.
по косинусам. 18. 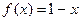 на
на  по синусам.
по синусам.
19.  на
на  по синусам.
по синусам.
20. Продолжить функцию  заданную в интервале
заданную в интервале  так, чтобы ее разложение на
так, чтобы ее разложение на  имело вид:
имело вид: 
ОТВЕТЫ
1. 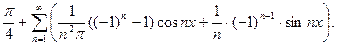 2.
2. 
3. а)  б)
б) 
4.  5.
5. 
6. 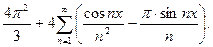 7.
7. 
8.  9.
9. 
10. 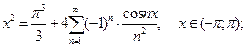

11.  12.
12. 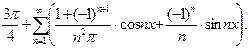
13.  14.
14. 
15.  16.
16. 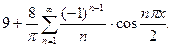
17.  18.
18. 
19. 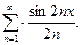 20.
20. 



 заданной на отрезке
заданной на отрезке  , кусочно-непрерывной на
, кусочно-непрерывной на 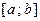 , имеющей в каждой точке
, имеющей в каждой точке  конечные односторонние производные, воспользуемся следующей с х е м о й:
конечные односторонние производные, воспользуемся следующей с х е м о й: , называемую
, называемую  периодическим продолжением функции
периодическим продолжением функции  на всю числовую ось, совпадающую с функцией
на всю числовую ось, совпадающую с функцией  любое число, удовлетворяющее неравенству:
любое число, удовлетворяющее неравенству:  .
. и его сумма вычисляется по формуле:
и его сумма вычисляется по формуле:
 в любой точке
в любой точке  где функция
где функция  (выбирая его из условия
(выбирая его из условия  во-вторых, доопределять функцию
во-вторых, доопределять функцию 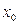 непрерывности функции
непрерывности функции  .
. и обладающую там указанными в теореме Дирихле – Дини свойствами непрерывности, можно на этом отрезке разложить как в ряд Фурье вида (17), вида (19), так и общего вида (14). Это объясняется возможностью продления функции
и обладающую там указанными в теореме Дирихле – Дини свойствами непрерывности, можно на этом отрезке разложить как в ряд Фурье вида (17), вида (19), так и общего вида (14). Это объясняется возможностью продления функции  или по закону четности, или нечетности, или какому–либо другому.
или по закону четности, или нечетности, или какому–либо другому. (22)
(22)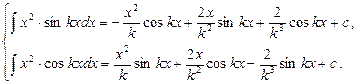 (23)
(23) получая разложение в ряд Фурье функции
получая разложение в ряд Фурье функции 
 периодической функции
периодической функции  равенством
равенством 
 у
у
 и кусочно непрерывно-дифференцируема, так как
и кусочно непрерывно-дифференцируема, так как  имеет в точках
имеет в точках  разрыв первого рода, а в остальных точках – непрерывна.
разрыв первого рода, а в остальных точках – непрерывна. и рассматриваемую функцию можно разложить в ряд Фурье (14), сходящийся в любой точке
и рассматриваемую функцию можно разложить в ряд Фурье (14), сходящийся в любой точке 





 при
при 
 – периодическую функцию
– периодическую функцию  определенную на
определенную на  и совпадающую с
и совпадающую с  (рис. 2).
(рис. 2). у
у

 является
является  и
и  терпят разрывы первого рода в точках вида
терпят разрывы первого рода в точках вида 
 с функцией
с функцией  получаем:
получаем:

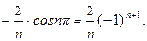


 разложить в ряд Фурье функцию:
разложить в ряд Фурье функцию:
 у
у
 -p О p х
-p О p х - 1
- 1 у
у



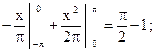











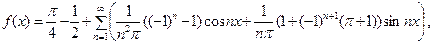
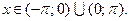
 построенный ряд имеет своей суммой число:
построенный ряд имеет своей суммой число:
 сумма данного ряда равна числу:
сумма данного ряда равна числу:
 ,
, 
 ее ряда Фурье.
ее ряда Фурье. периодическая, непрерывная на всей вещественной оси, дифференцируемая во всех точках
периодическая, непрерывная на всей вещественной оси, дифференцируемая во всех точках  в точках вида
в точках вида 
 имеет конечные односторонние производные:
имеет конечные односторонние производные:
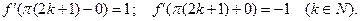


 терпит разрыв первого рода в любой из точек вида
терпит разрыв первого рода в любой из точек вида 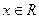 , включая точки разрыва функции
, включая точки разрыва функции  если
если 
 ;
; если
если 
 если
если  если
если
 у
у
 1
1
 то есть
то есть  вычисляем:
вычисляем:
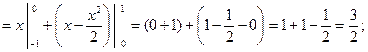




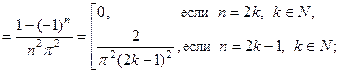






 (24)
(24)
 терпит разрыв первого рода в точках вида
терпит разрыв первого рода в точках вида  В точках
В точках  она имеет конечные односторонние производные:
она имеет конечные односторонние производные:

 при
при 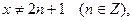

 у
у

 1
1













 при
при 
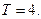
 у
у 3
3
 -7 -3 О 1 5 9 х
-7 -3 О 1 5 9 х -1 Рис. 7
-1 Рис. 7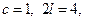 находим коэффициенты Фурье функции
находим коэффициенты Фурье функции 


 =
= 







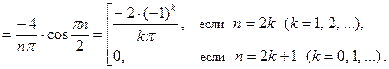



 у
у
 3
3
 1
1
 периодическим продолжением, где
периодическим продолжением, где  у
у


 имеет непрерывную производную
имеет непрерывную производную  во всех точках
во всех точках 
 Найдем предварительно его коэффициенты:
Найдем предварительно его коэффициенты:








 (25)
(25) при
при 
 при
при 
 при
при 
 при
при 
 .
. , заданную на интервале
, заданную на интервале  , разложить в ряд Фурье по синусам.
, разложить в ряд Фурье по синусам. график которой изображен на рис. 10.
график которой изображен на рис. 10. у
у


 -p О p 2p 3p х
-p О p 2p 3p х

 - p
- p




 на отрезке
на отрезке  разложить в ряд Фурье по косинусам.
разложить в ряд Фурье по косинусам. периодическую
периодическую  четную функцию
четную функцию  у
у
















 по синусам; б) на
по синусам; б) на 
 только по синусам, рассмотрим ее нечетное
только по синусам, рассмотрим ее нечетное  у
у 2p2
2p2




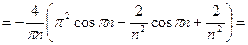

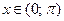 справедливо равенство:
справедливо равенство:
 у
у




 2p2
2p2









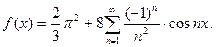
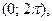 рассмотрим ее
рассмотрим ее  у
у
 -4p -2p О 2p 4p х Рис. 14
-4p -2p О 2p 4p х Рис. 14







 для функции
для функции 
 б)
б) 

 в ряд Фурье на
в ряд Фурье на  , найти сумму ряда: а)
, найти сумму ряда: а)  б)
б) 
 , заданная на отрезке
, заданная на отрезке  и продолженная четным образом, имеет ряд Фурье:
и продолженная четным образом, имеет ряд Фурье: (26)
(26)
 формула (26) принимает вид:
формула (26) принимает вид:
 б)
б) 
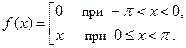 2.
2. 
 а) по косинусам, б) по синусам.
а) по косинусам, б) по синусам. по косинусам. 5.
по косинусам. 5.  на
на  по синусам.
по синусам. 7.
7.  на
на 
 на
на 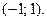 9.
9.  на
на 
 и
и  на интервале
на интервале  . Указание: воспользоваться разложением
. Указание: воспользоваться разложением  и почленным интегрированием.
и почленным интегрированием. 12.
12. 
 14.
14. 
 на
на  на
на 
 по косинусам. 18.
по косинусам. 18. 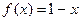 на
на  по синусам.
по синусам. на
на  заданную в интервале
заданную в интервале  так, чтобы ее разложение на
так, чтобы ее разложение на 
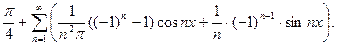 2.
2. 
 б)
б) 
 5.
5. 
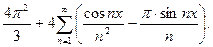 7.
7. 
 9.
9. 
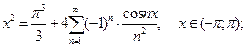

 12.
12. 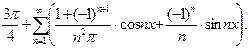
 14.
14. 
 16.
16. 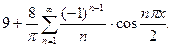
 18.
18. 
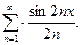 20.
20. 


