Пусть имеется вероятностное пространство (W, Å, P (×)) Определим на W числовую функцию X = X (w): каждому элементарному событию w приведено в соответствие вещественное число X (w).Такая функция называется случайной величиной. Мы ставим опыт, получаем элементарное событие w, смотрим, какое число X (w)= x было приведено ему в соответствие, и говорим: в опыте случайная величина X приняла значение x.
Рассмотрим простейший случай: число возможных значений случайной величины X конечно или счётно: x 1, ¼, xk, ¼ Такую случайную величину называют дискретной. Законом распределения дискретной случайной величины называют совокупность вероятностей её возможных значений: pk = P { X = xk }. Будем предполагать, что события { X = xk } содержатся в поле событий Å, и тем самым вероятности pk определены.
Очевидно, одно и только одно из своих значений случайная величина обязательно примет. Поэтому выполняется равенство
 pk =1,
pk =1,
называемое иногда условием нормировки в дискретном случае.
Задать случайную величину значит задать закон её распределения: т. е. указать её возможные значения и распределение вероятностей между ними.
В общем случае общепринятый способ задания случайной величины даёт так называемая функция распределения:
F (x)= P { X < x }.
Она указывает, какая вероятность досталась не отдельным точкам, а полуоси левее точки x, не включая саму точку x. Приходится дополнительно предполагать, что событие { X < x }ÎÅ, в противном случае функция распределения была бы не определена.
Дискретную случайную величину можно задавать её функцией распределения. Нетрудно сообразить, что это будет ступенчатая функция с разрывами в точках xk и скачками pk в этих точках:
F (x)= P { X < x }=  P { X = xk }=
P { X = xk }=  pk,
pk,
где суммирование ведётся по всем тем возможным значениям X, которые оказались меньше x.
Если существует такая функция p (x), которая позволяет представить функцию распределения интегралом:
F (x)=  p (x) dx,
p (x) dx,
то случайная величина X называется непрерывной, а p (x) – плотностью вероятности случайной величины X.
Функция распределения F (x) непрерывной случайной величины является непрерывной функцией (отсюда и название случайной величины), и, более того, – дифференцируемой функцией: F ¢(x)= p (x).
В более общем случае случайная величина X может принадлежать к смешанному типу: вероятность распределяется как между отдельными точками (дискретная составляющая), так и на интервалах (непрерывная составляющая). Если отдельным точкам xk достались вероятности pk, а остальная вероятность пошла на непрерывное распределение с линейной плотностью p (x), то:
F (x)= P { X < x }=  P { X = xk }+
P { X = xk }+  p (x) dx.
p (x) dx.
Если суммарная вероятность, доставшаяся точкам xk случайной величины X смешанного типа, равна A ( pk = A), а на непрерывное распределение X уходит вероятность B, (
pk = A), а на непрерывное распределение X уходит вероятность B, ( p (x) dx = B), то A + B =1.
p (x) dx = B), то A + B =1.
Можно считать, что случайная величина X является смесью двух случайных величин: дискретной Y с возможными значениями xk и вероятностями  pk и непрерывной Z с плотностью
pk и непрерывной Z с плотностью  p (x). Функция распределения X имеет вид: F (x)= AFY (x)+ BFZ (x).
p (x). Функция распределения X имеет вид: F (x)= AFY (x)+ BFZ (x).
Вообще, если имеются случайные величины Xi, i =1, 2, ¼, n с функциями
F (x)=  AiFXi (x),
AiFXi (x),
где числа Ai удовлетворяют условиям: 0£ Ai £1, A 1+ A 2+¼+ An =1, и играют роль весовых множителей, они регулируют вклад в смесь отдельных составляющих. Функция F (x), очевидно, обладает необходимыми свойствами функции распределения и может задавать случайную величину.
Основные свойства функции распределения F ( x )
и плотности вероятности p ( x )
1°. Считаем, что случайная величина X или совсем не принимает значений ±¥ или почти наверное их не принимает: P { X =+¥}= P { X =-¥}=0. При этом предположении:
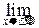 F (x)= F (-¥)=0,
F (x)= F (-¥)=0,  F (x)= F (+¥)=1.
F (x)= F (+¥)=1.
2°. F (x) – монотонно-неубывающая функция:
x 1< x 2 Þ F (x 1)£ F (x 2).
Действительно: { X < x 2}={ X < x 1}+{ x 1£ X < x 2}. Справа стоит сумма двух несовместимых событий. Поэтому:
P { X < x 2}= P { X < x 1}+ P { x 1£ X < x 2},
или:
F (x 2)= F (x 1)+ P { x 1£ X < x 2}
и неравенство F (x 2)³ F (x 1) следует из неотрицательности вероятности P { x 1£ X <
< x 2}.
3°. В доказательстве второго свойства мы выразили через функцию распределения вероятность попадания случайной величины X в полуоткрытый интервал:
P { x 1£ X < x 2}= F (x 2)- F (x 1).
4°. Перепишем последнее равенство, взяв x 1= x, x 2= x +e, e>0:
P { x £ X < x +e}= F (x +e)- F (x).
Перейдём здесь к пределу при e®0: P { X = x }=  F (x +e)- F (x)= F (x +0)- F (x). Таким образом, для любой случайной величины X вероятность любого конкретного значения равна скачку F (x +0)- F (x) её функции распределения в точке x. Во всех точках непрерывности F (x) этот скачок и, следовательно, вероятность P { X = x }, равны нулю. Для непрерывных случайных величин все точки таковы, и ни одной из них не досталось положительной вероятности.
F (x +e)- F (x)= F (x +0)- F (x). Таким образом, для любой случайной величины X вероятность любого конкретного значения равна скачку F (x +0)- F (x) её функции распределения в точке x. Во всех точках непрерывности F (x) этот скачок и, следовательно, вероятность P { X = x }, равны нулю. Для непрерывных случайных величин все точки таковы, и ни одной из них не досталось положительной вероятности.
Если мы наблюдаем непрерывную случайную величину и получили значение X = x, то мы получили пример события A ={ X = x }, вероятность которого равна нулю, которое, однако, произошло, а событие  ={ X ¹ x }, вероятность которого рана единице, не произошло. Ясно, что повторить появление события A почти наверное не удастся.
={ X ¹ x }, вероятность которого рана единице, не произошло. Ясно, что повторить появление события A почти наверное не удастся.
Так как функция распределения определена равенством F (x)= P { X < x }, где под знаком вероятности стоит строгое неравенство, то вероятность, возможно сосредоточенная в точке x, не учитывается, поэтому F (x) – функция, непрерывная слева:
 F (x -e)= F (x -0)= F (x).
F (x -e)= F (x -0)= F (x).
5°. Теперь нетрудно выразить через F (x) вероятность попадания случайной величины в произвольный интервал:
P { x 1£ X £ x 2}= F (x 2+0)- F (x 1),
P { x 1< X < x 2}= F (x 2)- F (x 1+0),
P { x 1< X £ x 2}= F (x 2+0)- F (x 1+0).
6°. Плотность вероятности p (x) неотрицательна. Это следует из монотонного неубывания F (x).
7°. Переходя к пределу при x ®+¥ в равенстве F (x)=  p (x) dx, и учитывая, что F (+¥)=1, получим условие нормировки для непрерывной случайной величины:
p (x) dx, и учитывая, что F (+¥)=1, получим условие нормировки для непрерывной случайной величины:
 p (x) dx =1.
p (x) dx =1.
Геометрический смысл этого равенства: площадь под кривой плотности вероятности всегда равна единице.
8°. Общее правило вычисления вероятностей для дискретной и непрерывной случайной величины: если A –– некоторое числовое множество на вещественной оси, то
P { X Î A }= 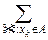 P { X = xk },
P { X = xk },
P { X Î A }=  p (x) dx
p (x) dx
и ясно, что в непрерывном случае вероятность событий { X Î A } определена лишь для таких множеств A, для которых имеет смысл интеграл  p (x) dx.
p (x) dx.
9°. Мы считаем, что задавая произвольную функцию F (x) с обязательными свойствами функции распределения: монотонное неубывание, непрерывность слева, F (-¥)=0, F (+¥)=1, – мы задаём некоторую случайную величину. Если F (x) – ступенчатая функция, то она задаёт дискретную случайную величину: точки скачков – её возможные значения, величины скачков – их вероятности.
Дискретную случайную величину можно задать таблицей её возможных значений и их вероятностей: xk, pk, k =1, 2, ¼, n, лишь бы были " pk ³0 и  pk =1.
pk =1.
Непрерывную случайную величину можно задать плотностью вероятности p (x). В качестве таковой может служить любая неотрицательная функция, удовлетворяющая условию нормировки:  p (x) dx =1.
p (x) dx =1.
Основные случайные величины
Любой сходящийся интеграл от неотрицательной функции порождает непрерывное распределение. Именно, если  j(x) dx = I, то роль плотности играет
j(x) dx = I, то роль плотности играет
p (x)= 
| |

j(
x), если
x Î
A,
0, если
x Ï
A.
Любая конечная сумма или сходящийся ряд с неотрицательными слагаемыми порождает дискретное распределение. Именно: если  qk = S, то роль дискретных вероятностей играют pk =
qk = S, то роль дискретных вероятностей играют pk = 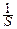 qk, а в качестве xk можно взять любые числа; наиболее простой выбор: xk = k.
qk, а в качестве xk можно взять любые числа; наиболее простой выбор: xk = k.
Рассмотрим конкретные примеры.
1°. Равномерное распределение. Его порождает интеграл  dx = b - a.
dx = b - a.
p (x)= 
| |

, если
x Î[
a,
b ],
0, если
x Ï[
a,
b ].
Этот закон распределения будем обозначать R (a, b); числа a и b называются параметрами распределения. Тот факт, что случайная величина X равномерно распределена на отрезке [ a, b ], будем обозначать следующим образом: X ~ R (a, b).
В частности, плотность случайной величины X ~ R (0, 1) имеет наиболее простой вид:
p (x)= 
| |
1, если
x Î[0, 1],
0, если
x Ï[0, 1].
Функция распределения такой случайной величины равна:
F (x)= 
| |
0, если
x <0,
x, если 0£
x £1,
1, если
x >0.
Если мы наугад выбираем точку на отрезке [0, 1], то её абсцисса x является конкретным значением случайной величины X ~ R (0, 1). Слово ''наугад" имеет в теории вероятностей терминологическое значение и говорится с целью подчеркнуть, что соответствующая непрерывная случайная величина распределена равномерно, или дискретная случайная величина имеет конечное число N возможных равновероятных значений.
2°. Экспоненциальное распределение.
Его порождает интеграл  e -m xdx =
e -m xdx =  , m>0.
, m>0.
p (x)= 
| |
Плотность вероятности, очевидно, равна
m e -m x, если x ³0,
0, если x <0,
F (x)= 
| |
а функция распределения:
1-m e -m x, если x ³0,
0, если x <0.
То обстоятельство, что случайная величина распределена по экспоненциальному закону, будем записывать так: X ~ Exp (m), m называется параметром распределения (m>0).
3°. Распределение Коши. Его порождает интеграл 
 dx =p.
dx =p.
Плотность вероятности: p (x)=  , -¥< x <+¥.
, -¥< x <+¥.
4°. Гамма-распределение. Его порождает интеграл, который определяет гамма-функцию: G(l)=  e - tt l-1 dt, l>0. Выполним в этом интеграле замену переменной, положим: t =m x, m>0:
e - tt l-1 dt, l>0. Выполним в этом интеграле замену переменной, положим: t =m x, m>0:
G(l)=ml  e -m xx l-1 dx.
e -m xx l-1 dx.
p (x)= 
| |
Соответствующая плотность вероятности равна:
 x l-1 e -m x, если x >0,
x l-1 e -m x, если x >0,
0, если x £0.
Будем обозначать это распределение G(l, m), l и m – параметры распределения (l>0, m>0).
5°. Нормальное распределение. Его порождает интеграл Пуассона:
I = 
 dx =
dx =  .
.
Докажем это равенство. Интеграл бы легко вычислялся, если бы подынтегральное выражение содержало множитель x. Такой множитель можно ввести под знак интеграла с помощью следующего остроумного приёма.
Запишем квадрат интеграла в следующем виде:
I 2= 
 dx ×
dx × 
 dy,
dy,
а теперь представим произведение интегралов как двойной интеграл:
I 2= 

 dxdy.
dxdy.
Перейдём в этом интеграле к полярным координатам. Положим: x = r cosj, y =
= r sinj, и ещё вспомним, что абсолютная величина якобиана при переходе от декартовых координат к полярным равна r. Заметим, наконец, что областью интегрирования двойного интеграла является вся плоскость, так что границы изменения переменных r и j, соответственно, таковы: r Î[0; +¥), jÎ[0; 2p). Поэтому:
I 2=  d j
d j 
 rdr.
rdr.
Теперь легко убедиться, что 
 rdr =1, а потому I 2=2p.
rdr =1, а потому I 2=2p.
Распределение с плотностью
p (x)= 
 , x Î(-¥; +¥)
, x Î(-¥; +¥)
называется стандартным нормальным законом и обозначается N (0, 1).
Ему соответствует функция распределения:
F 0(x)= 

 dx.
dx.
Обычно принято табулировать интеграл
F(x)= 

 dx,
dx,
называемый интегралом ошибок или интегралом Лапласа. Функция распределения стандартного нормального закона просто выражается через этот интеграл:
F 0(x)=  +
+  F(x).
F(x).
Если в интеграл Пуассона ввести параметры масштаба и сдвига с помощью замены переменной, заменив x на  , то он примет вид:
, то он примет вид:


 dx =1.
dx =1.
Случайную величину с плотностью вероятности
p (x)= 
 , x Î(-¥; +¥),
, x Î(-¥; +¥),
называют нормально распределённой случайной величиной или просто нормальной. Соответствующий ей закон распределения обозначают N (a, s), a и s – параметры распределения (s>0, a – любое вещественное число).
График p (x) представлен на рис. 1.
a – точка максимума p (x), его значение равно  . Так как площадь под кривой всегда равна единице, то чем меньше s, тем больше вероятности сосредоточивается вблизи максимума. Таким образом, устанавливаем вероятностный смысл параметров нормального закона: областью наиболее вероятных значений нормальной случайной величины является окрестность точки a, а s указывает на степень концентрации вероятности в окрестности точки a – чем меньше s, тем менее вероятны заметные отклонения X от a.
. Так как площадь под кривой всегда равна единице, то чем меньше s, тем больше вероятности сосредоточивается вблизи максимума. Таким образом, устанавливаем вероятностный смысл параметров нормального закона: областью наиболее вероятных значений нормальной случайной величины является окрестность точки a, а s указывает на степень концентрации вероятности в окрестности точки a – чем меньше s, тем менее вероятны заметные отклонения X от a.
Функцию распределения произвольного нормального закона легко выразить через интеграл Лапласа. Для этого нужно в выражении для функции распределения
F (x)= 

 dx
dx
выполнить замену переменной, положив  = y:
= y:
F (x)= 

 dy =
dy =  +
+  F(
F( ).
).
6°. Геометрическое распределение. Его порождает геометрическая прогрессия: 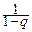 =
=  qk -1, 0< q <1.
qk -1, 0< q <1.
Соответствующая дискретная случайная величина имеет возможные значения xk = k, k =1, 2, ¼ с вероятностями pk =(1- q) qk -1. Обозначение геометрического распределения: G (q), q – параметр распределения (0< q <1).
7°. Пуассоновское распределение. Его порождает разложение в ряд показательной функции: e l= 
 , l>0, которому отвечает дискретная случайная величина, принимающая целые неотрицательные значения xk = k, k =0, 1, 2, ¼ с вероятностями pk =
, l>0, которому отвечает дискретная случайная величина, принимающая целые неотрицательные значения xk = k, k =0, 1, 2, ¼ с вероятностями pk =  .
.
Будем обозначать это распределение через P(l), l – параметр распределения (l>0).
8°. Биномиальное распределение. Его порождает формула бинома Ньютона: (p + q) n = 
 pmqn - m.
pmqn - m.
Чтобы сумма вероятностей распределения pk равнялась единице и все они были положительными, возьмём p >0, q >0, p + q =1, т. е. q =1- p. Возможными значениями будем считать xk = k, k =0, 1, 2, ¼, n, а их вероятностями – pk =  pkqn - k. Обозначим это распределение B (n, p), n и p – параметры распределения (0< p <1, n ÎN, т. е. n – натуральное число).
pkqn - k. Обозначим это распределение B (n, p), n и p – параметры распределения (0< p <1, n ÎN, т. е. n – натуральное число).
Биномиальная случайная величина появляется, например, в схеме Бернулли, называемой также схемой последовательных независимых испытаний. Состоит она в следующем: осуществляется некоторый комплекс условий, при котором мы имеем одно и только одно из двух событий: либо "успех", либо "неудачу", причём вероятность "успеха" равна p, вероятность "неудачи" равна q =
=1- p; эта попытка независимым образом повторяется n раз. Считая опытом все n попыток, можем считать элементарным событием опыта цепочку длины n, полученных в результате опыта "успехов" (У) и "неудач" (Н): УУУННУ
Н¼У.
Определим случайную величину X, задав её как число успехов в одном опыте. Событию { X = k } благоприятствуют те элементарные события, которые содержат "успех" ровно k раз, а "неудачу" – остальные n - k раз. Число таких благоприятствующих событию { X = k } элементарных событий, равно, очевидно,  , а вероятности всех их одинаковы и по теореме умножения для независимых событий равны pkqn - k. Окончательно получаем: P { X = k }=
, а вероятности всех их одинаковы и по теореме умножения для независимых событий равны pkqn - k. Окончательно получаем: P { X = k }=  pkqn - k, а возможными значениями случайной величины X оказываются числа xk = k, k =
pkqn - k, а возможными значениями случайной величины X оказываются числа xk = k, k =
=0, 1, 2, ¼ n. Таким образом, число успехов X в схеме Бернулли – биномиальная случайная величина: X ~ B (n, p).
Пусть имеется вероятностное пространство (W, Å, P (×)) и рассматривается некоторое событие A. Обозначим его вероятность P (A)= p. Пусть испытание независимым образом повторяется n раз, причём событие A в этих n последовательных попытках наблюдалось k раз. Число k называется абсолютной частотой события A. Оно является конкретным значением случайной величины X, определённой на серии из n независимых испытаний. Ничто не мешает объявить событие A "успехом", а событие  – "неудачей". Это превращает последовательность из n испытаний в схему Бернулли, а абсолютная частота события A оказывается распределённой по закону Бернулли.
– "неудачей". Это превращает последовательность из n испытаний в схему Бернулли, а абсолютная частота события A оказывается распределённой по закону Бернулли.
Геометрическое распределение также просто связано со схемой Бернулли: будем повторять попытку до появления первого "успеха". Элементарным событием в таком опыте является цепочка, у которой "успех" расположен только на последнем (k -м) месте, а на всех предыдущих местах (а их k -1) – только "неудачи": ННННН¼НУ. Свяжем с этим опытом случайную величину X – общее число попыток в опыте. Очевидно, значениями этой случайной величины могут быть xk = k, k =1, 2, 3, ¼, а их вероятности pk = qk -1 p, что и совпадает с геометрическим распределением G (p).


 pk =1,
pk =1, P { X = xk }=
P { X = xk }=  pk,
pk, p (x) dx,
p (x) dx, p (x) dx = B), то A + B =1.
p (x) dx = B), то A + B =1. pk и непрерывной Z с плотностью
pk и непрерывной Z с плотностью  p (x). Функция распределения X имеет вид: F (x)= AFY (x)+ BFZ (x).
p (x). Функция распределения X имеет вид: F (x)= AFY (x)+ BFZ (x). AiFXi (x),
AiFXi (x),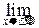 F (x)= F (-¥)=0,
F (x)= F (-¥)=0,  F (x)= F (+¥)=1.
F (x)= F (+¥)=1. F (x +e)- F (x)= F (x +0)- F (x). Таким образом, для любой случайной величины X вероятность любого конкретного значения равна скачку F (x +0)- F (x) её функции распределения в точке x. Во всех точках непрерывности F (x) этот скачок и, следовательно, вероятность P { X = x }, равны нулю. Для непрерывных случайных величин все точки таковы, и ни одной из них не досталось положительной вероятности.
F (x +e)- F (x)= F (x +0)- F (x). Таким образом, для любой случайной величины X вероятность любого конкретного значения равна скачку F (x +0)- F (x) её функции распределения в точке x. Во всех точках непрерывности F (x) этот скачок и, следовательно, вероятность P { X = x }, равны нулю. Для непрерывных случайных величин все точки таковы, и ни одной из них не досталось положительной вероятности. ={ X ¹ x }, вероятность которого рана единице, не произошло. Ясно, что повторить появление события A почти наверное не удастся.
={ X ¹ x }, вероятность которого рана единице, не произошло. Ясно, что повторить появление события A почти наверное не удастся. F (x -e)= F (x -0)= F (x).
F (x -e)= F (x -0)= F (x).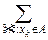 P { X = xk },
P { X = xk }, p (x) dx
p (x) dx
 j(x), если x Î A,
j(x), если x Î A, qk = S, то роль дискретных вероятностей играют pk =
qk = S, то роль дискретных вероятностей играют pk = 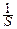 qk, а в качестве xk можно взять любые числа; наиболее простой выбор: xk = k.
qk, а в качестве xk можно взять любые числа; наиболее простой выбор: xk = k. dx = b - a.
dx = b - a. , если x Î[ a, b ],
, если x Î[ a, b ],
 e -m xdx =
e -m xdx =  , m>0.
, m>0.
 dx =p.
dx =p. , -¥< x <+¥.
, -¥< x <+¥.
 x l-1 e -m x, если x >0,
x l-1 e -m x, если x >0, dx =
dx =  .
. dy,
dy, dxdy.
dxdy. d j
d j  rdr.
rdr.


 +
+  , то он примет вид:
, то он примет вид:
 dx =1.
dx =1.






 ).
).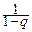 =
=  qk -1, 0< q <1.
qk -1, 0< q <1.
 , l>0, которому отвечает дискретная случайная величина, принимающая целые неотрицательные значения xk = k, k =0, 1, 2, ¼ с вероятностями pk =
, l>0, которому отвечает дискретная случайная величина, принимающая целые неотрицательные значения xk = k, k =0, 1, 2, ¼ с вероятностями pk =  .
.
 pmqn - m.
pmqn - m. pkqn - k. Обозначим это распределение B (n, p), n и p – параметры распределения (0< p <1, n ÎN, т. е. n – натуральное число).
pkqn - k. Обозначим это распределение B (n, p), n и p – параметры распределения (0< p <1, n ÎN, т. е. n – натуральное число).