

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пусть теперь система координат OXYZ перемещается относительно неподвижной (абсолютной) системы координат OaXYZ таким образом, что соответствующие оси всегда остаются параллельными: OX // OaX, OY // OaY, OZ // OaZ (рис. 11). Система координат Oxyz, по-прежнему, жестко связана с твердым телом. Тогда положение некоторой точки P тела, совершающего произвольное перемещение, определится из соотношения:
 , (2)
, (2)
где  - радиус-вектор центра O в неподвижной системе координат,
- радиус-вектор центра O в неподвижной системе координат,  - радиус-вектор точки P в системе координат Oxyz.
- радиус-вектор точки P в системе координат Oxyz.
 | |||
 | |||
Теперь, если задать  и
и  , то будет задано движение твердого тела в абсолютной системе координат.
, то будет задано движение твердого тела в абсолютной системе координат.
Задача
Определить конечное положение стержня AB из предыдущей задачи, если стержень после поворота на угол θ = 600 вокруг оси OZ совершил поступательное перемещение 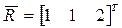 .
.
Решение
Введем абсолютную систему координат OaXYZ так, чтобы в начальном положении системы координат OaXYZ и OXYZ совпадали. Тогда конечные положения точек A и B стержня будут получены из соотношений:
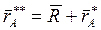 ,
, 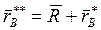 .
.
Выполняя вычисления, получим:
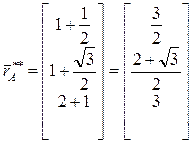 ,
, 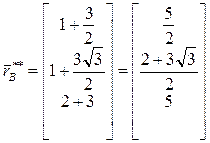 .
.
Начальное, промежуточное и конечное положения стержня, а также его перемещения изображены на рис. 12.
2.4. Скорость точки твердого тела в случае его произвольного движения
Пусть задан радиус-вектор некоторого центра O твердого тела 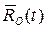 и матрица поворота A(t). Тогда скорость любой точки P, принадлежащей этому телу определится из соотношения:
и матрица поворота A(t). Тогда скорость любой точки P, принадлежащей этому телу определится из соотношения:
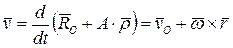 , (3)
, (3)
где 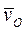 - абсолютная скорость центра O,
- абсолютная скорость центра O, 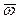 - угловая скорость твердого тела. Координаты вектора
- угловая скорость твердого тела. Координаты вектора 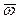 в системе координат OaXYZ определяются как элементы кососимметрической матрицы5
в системе координат OaXYZ определяются как элементы кососимметрической матрицы5
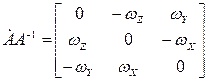 . (4)
. (4)
Скорость центра 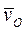 и угловая скорость
и угловая скорость 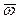 являются величинами, общими для всего твердого тела. Согласно (3), с их помощью можно вычислить скорость любой точки твердого тела относительно неподвижного начала отсчета.
являются величинами, общими для всего твердого тела. Согласно (3), с их помощью можно вычислить скорость любой точки твердого тела относительно неподвижного начала отсчета.
|
|
Задача
Вал, на котором укреплена зенитная пушка, вращается вокруг своей оси OX* по закону 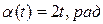 и одновременно поворачивается вокруг оси OZ неподвижной системы координат OXYZ по закону
и одновременно поворачивается вокруг оси OZ неподвижной системы координат OXYZ по закону 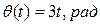 (рис. 13). Определить угловую скорость вала.
(рис. 13). Определить угловую скорость вала.
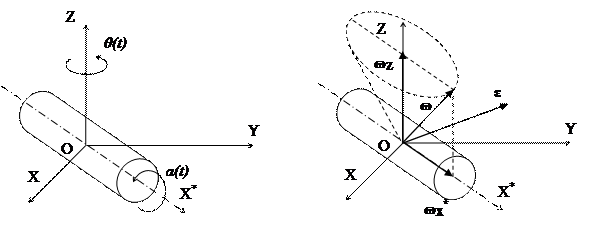
Рис. 14
Рис. 13
Решение
По условию задачи, вал вращается вокруг неподвижной точки O. Найдем матрицу поворота вала:
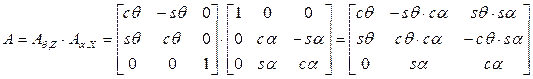 .
.
Вектор угловой скорости вала 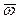 найдем согласно (4). Для этого выполним следующие вычисления:
найдем согласно (4). Для этого выполним следующие вычисления:
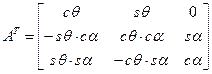 ;
; 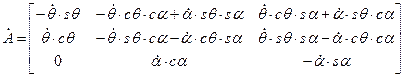 .
.
Учитывая, что 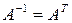 , получаем:
, получаем:
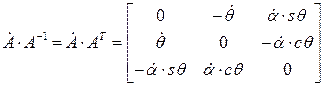 , откуда
, откуда 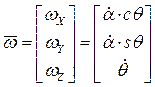 .
.
Модуль вектора угловой скорости: 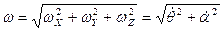 . Подставляя исходные данные
. Подставляя исходные данные 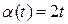 ,
, 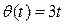 в полученные соотношения, окончательно будем иметь:
в полученные соотношения, окончательно будем иметь:
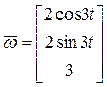 ,
, 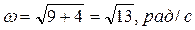 .
.
Таким образом, вектор угловой скорости вала имеет постоянную величину 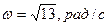 и вращается вокруг оси OZ по закону
и вращается вокруг оси OZ по закону 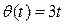 (рис. 14).
(рис. 14).
2.5. Ускорение точки твердого тела в случае его произвольного движения
Ускорение точки P, принадлежащей твердому телу, вычисляется в соответствии с соотношением:
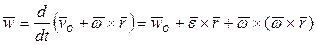 , (5)
, (5)
где 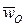 - ускорение центра O,
- ускорение центра O, 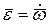 - угловое ускорение твердого тела. Слагаемое
- угловое ускорение твердого тела. Слагаемое 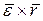 называют вращательным, а
называют вращательным, а 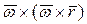 - осестремительным ускорением. Ускорение центра
- осестремительным ускорением. Ускорение центра 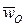 и угловое ускорение
и угловое ускорение 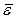 являются величинами, общими для всего твердого тела.
являются величинами, общими для всего твердого тела.
Задача
Вычислить угловое ускорение вала из задачи п. 2.4.
Решение
Угловое ускорение найдем, продифференцировав по времени t вектор угловой скорости:
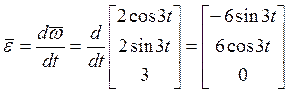 .
.
Модуль углового ускорения: 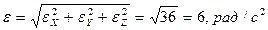 . Таким образом, угловое ускорение вала постоянно по величине, находится в плоскости OXY нормально к
. Таким образом, угловое ускорение вала постоянно по величине, находится в плоскости OXY нормально к 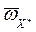 и вращается вокруг оси OZ вместе с вектором
и вращается вокруг оси OZ вместе с вектором 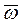 (рис. 14).
(рис. 14).
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!