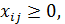Направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности называется линейным программированием (ЛП).
К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.
Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например:
§ задача об оптимальном использовании ресурсов при производственном планировании;
· задача о смесях (планирование состава продукции);
· задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");
· транспортные задачи (анализ размещения предприятия, перемещение грузов).
· задача о назначении.
Математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.
В общем виде модель записывается следующим образом:
целевая функция:
 (1.1)
(1.1)
ограничения:
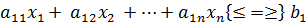 ,
,
 ,
,
………………………….. ……….. (1.2)
 ;
;
требование неотрицательности переменных
 , j=
, j=  (1.3)
(1.3)
При этом 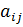 ,
,  ,
, 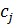
 - заданные постоянные величины.
- заданные постоянные величины.
Задача состоит в нахождении оптимального значения функции (1) при соблюдении ограничений (1.2) и (1.3).
Систему ограничений (2) называют функциональными ограничениями задачи, а ограничения (3) - прямыми.
Вектор  , удовлетворяющий ограничениям (2) и (3), называется допустимым решением (планом) задачи линейного программирования. План
, удовлетворяющий ограничениям (2) и (3), называется допустимым решением (планом) задачи линейного программирования. План  , при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным.
, при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным.
С каждой задачей ЛП связывают другую задачу ЛП, которая записывается по определенным правилам и называется двойственной задачей ЛП.
Двойственной к задаче ЛП (1)—(3) является задача
 (1.4)
(1.4)
 , j=
, j=  (1.5)
(1.5)

 (1.6)
(1.6)
Соответственно, двойственной к задаче ЛП (1.4)—(1.6) является задача (1.1)—(1.3). Каждой переменной (специальному ограничению) исходной задачи соответствует специальное ограничение (переменная) двойственной задачи. Если исходная задача ЛП имеет решение, то имеет решение и двойственная к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.
1.2. Задача оптимального распределения ресурсов при планировании выпуска продукции предприятия. Симплексный метод решения задачи линейного программирование. Надстройка ПОИСК РЕШЕНИЯ.
Пример 1. Предположим, что для производства двух видов продукции А и В используются три вида ресурсов. На изготовление единицы изделия А расходуется a1, а2 и а 3 кг ресурсов соответствующего вида, на изготовление единицы изделия В расходуется b1, b2 и b3 кг ресурсов. На складе фирмы наличные объемы ресурсов соответствующего вида составляют p1, р2 и рз кг. От реализации единицы готовой продукции вида А фирма имеет прибыль в размере с1 рублей, а от единицы продукции вида В - с2 рублей. Требуется:
1. Найти такие объемы производства продукции А и В, при которых достигается максимум суммарной прибыли от реализации. При этом количество используемых ресурсов на производство продукции не должно превосходить их наличного количества;
2. Составить математическую модель задачи линейного программирования
3. Найти решение задачи симплекс – методом.
| a1
| а2
| а 3
| b1
| b2
| B3
| p1
| р2
| рз
| с1
| с2
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
1) Математическая модель задачи:
Пусть х1 - число единиц продукции вида А и х2 – число единиц продукции вида В. Требуется найти максимум целевой функции
 при следующей системе ограничений:
при следующей системе ограничений:
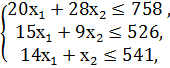

2) Решим задачу симплекс - методом.
Запишем задачу в форме основной задачи линейного программирования, т.е. перейдем от ограничений – неравенств к ограничениям- равенствам. Для этого необходимо ввести четыре дополнительные переменные 
Найти Zmax=10 х1 +2 х2, если:
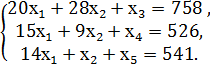
При условиях 
Введем в рассмотрение векторы: 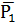 =
=  ;
;  =
=  ;
;  =
=  ;
;
 =
=  ;
;  =
= 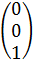 , координатами которых будут коэффициенты при неизвестных, взятые из левой части системы ограничений, и вектор
, координатами которых будут коэффициенты при неизвестных, взятые из левой части системы ограничений, и вектор  =
= 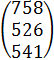 , координатами которого являются свободные члены системы ограничений.
, координатами которого являются свободные члены системы ограничений.
 - линейно- независимые векторы. Это допустимый базис задачи.
- линейно- независимые векторы. Это допустимый базис задачи.
Базисом является- 
Опорный план 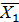 ={0,0,758,526,541}, т.е. свободные переменные
={0,0,758,526,541}, т.е. свободные переменные  ,
, 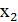 полагаем равными нулю, а базисные
полагаем равными нулю, а базисные  - координатам вектора
- координатам вектора 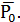
Симплекс – таблица первой итерации
| | | |
|
|
|
|
|
| | Базисные неизвестные
| Свободные члены
| х1
| х2
| х3
| х4
| х5
|
|
| х3
|
|
|
|
|
|
|
|
| х4
|
|
|
|
|
| 0
|
|
| х5
|
|
|
|
|
|
|
|
|
|
| -10
| -2
|
|
|
|
Последняя строка таблицы (индексная строка) рассчитывается следующим образом:
Для столбца свободных членов - умножаем первый и третий столбцы и прибавляем свободный член целевой функции;
Для столбца х1- умножаем первый и четвертый столбцы и вычитаем коэффициент при х1 целевой функции;
Для столбца х2- умножаем первый и пятый столбцы и вычитаем коэффициент при х2 целевой функции;
Признак оптимальности плана - отсутствие отрицательных чисел в индексной строке. Если план не оптимален, то его улучшают, для чего находят направляющие столбец и строку.
1) Максимальное по абсолютной величине отрицательное индексное число (-10), ему соответствует направляющий столбец (), Переменную х1 следует ввести в базис следующей симплекс таблицы.
Направляющая строка характеризуется наименьшим положительным частным от деления элементов столбца Р0 на соответствующие элементы направляющего столбца.
Так как  = min{37,9;35,066;38,64}=35 то направляющей будет строка ().
= min{37,9;35,066;38,64}=35 то направляющей будет строка ().
Из базиса следует вывести переменную x4. Разрешающий элемент 15.
Симплекс – таблица второй итерации
| Базисные неизвестные
| Свободные члены
| х1
| х2
| х3
| х4
| х5
|
| Х3
| 56,66
|
| 0,4
|
| -1,33
|
|
| Х1
| 35,066
|
| 0,6
|
| 0,066
|
|
| х5
| 50,066
|
| -7,4
|
| -0,93
|
|
| | 350,66
|
|
|
| 0,666
|
|
Заполняем симплекс таблицу второй итерации. Сначала делим направляющую строку на разрешающий элемент. Затем умножаем полученную строку на (-20) и прибавляем к первой строке, умножаем на (-14) и прибавляем к третьей, умножаем на (10) и прибавляем к индексной строке. Это заполнение симплекс таблицы по методу Гаусса.
Получен следующий опорный план: 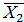 ={35,066, 0, 56,66, 0, 50,066}. Он является оптимальным, так в индексной строке нет отрицательных чисел. Zmax= 350,66
={35,066, 0, 56,66, 0, 50,066}. Он является оптимальным, так в индексной строке нет отрицательных чисел. Zmax= 350,66
Вычислительная процедура симплекс-метода является итерационным процессом. Если задача содержит несколько переменных и ограничений, то этот процесс очень громоздок. Во многие практические задачи входят десятки переменных и ограничений (иногда намного больше), и ясно, что неразумно решать эти задачи вручную. Симплекс-метод - это метод для электронно-вычислительных машин. Не случайно развитие теории линейного программирования совпало по времени с развитием электронно-вычислительных машин. Без них теория имела бы весьма узкую область приложений.
Рассмотрим решение задачи оптимизации с помощью надстройки Поиск решения в средеEXCEL
Поиск решения — это надстройка Excel, которая позволяет решать оптимизационные задачи. Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите команду Сервис => Надстройки и активизируйте надстройку Поиск решения. Если же этой надстройки нет, в диалоговом окне Надстройки, необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки Excel(или Office) установить надстройку Поиск решения.
После выбора команд Сервис => Поиск решения появится диалоговое окно Поиск решения.
Основные параметры диалогового окна Поиск решения:
• Установить целевую ячейку;
• Изменяя ячейки;
• Ограничения.
Сначала нужно заполнить поле Установить целевую ячейку. Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или установить конкретное значение.
Второй важный параметр средства Поиск решения — это параметр Изменяя ячейки. Здесь указываются ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. Для поиска решения можно указать до 200 изменяемых ячеек. К этим ячейкам предъявляется два основных требования: они не должны содержать формул и изменение их значений должно отражаться на изменении результата в целевой ячейке. Другими словами, целевая ячейка зависит от изменяемых ячеек.
Третий параметр, который нужно вводить на вкладке Поиск решения, — это Ограничения.
Для решения задачи необходимо:
1) указать адреса ячеек, в которые будет помещен результат решения (установить изменяемые ячейки);
2) ввести исходные данные;
3) ввести зависимость для целевой функции;
4) ввести зависимости для ограничений;
5) запустить команду Поиск решения;
6) назначить ячейку для целевой функции (установить целевую ячейку);
7) ввести ограничения;
8) ввести параметры для решения ЗЛП.
1. Обозначим через  , х 2число единиц продукции каждого вида. В нашей задаче оптимальные значения вектора
, х 2число единиц продукции каждого вида. В нашей задаче оптимальные значения вектора 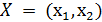 будут помещены в ячейках B3:C3, а оптимальное значение целевой функции - в ячейке D4.
будут помещены в ячейках B3:C3, а оптимальное значение целевой функции - в ячейке D4.
2. Введем исходные данные задачи, как показано на рис. 1.1.
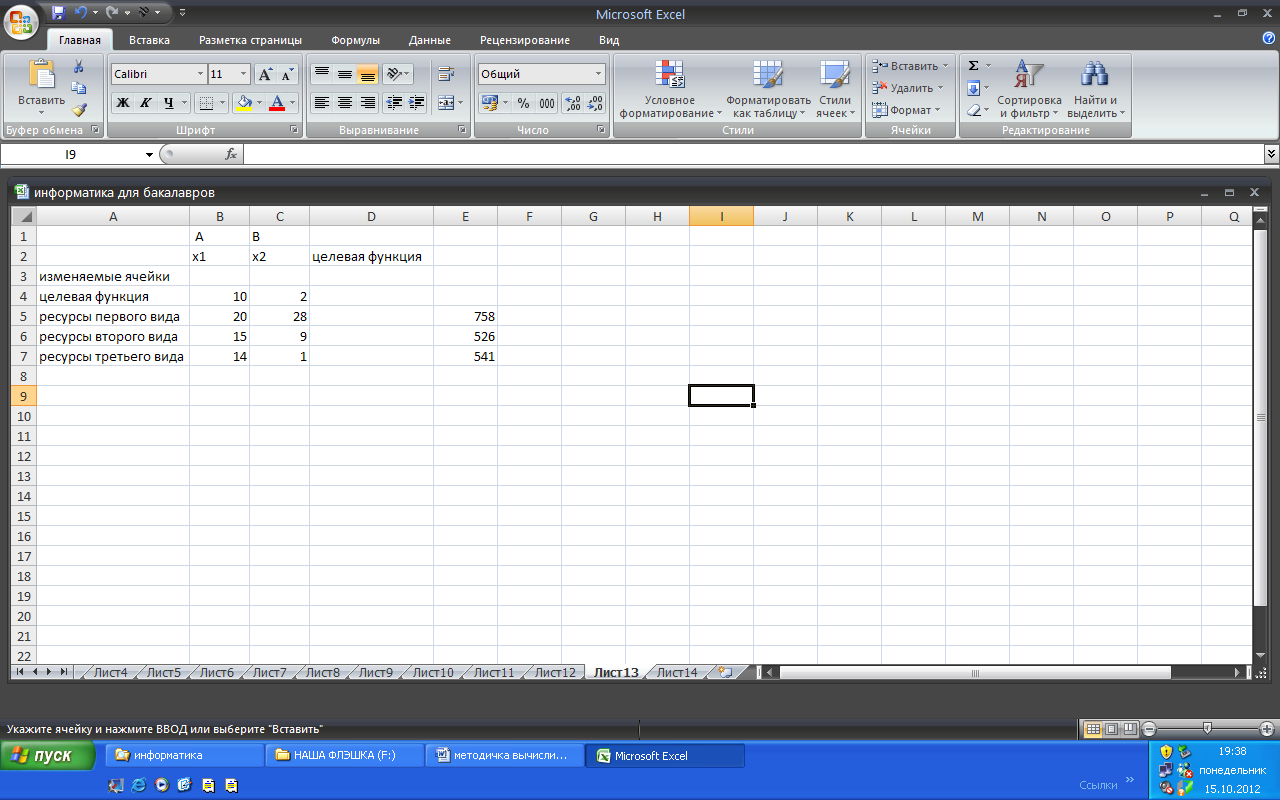
Рис. 1.1. Введены исходные данные
3. Введем зависимость для целевой функции.
Поместим курсор в ячейку DЗ, произойдет выделение ячейки.
Поместим курсор на кнопку мастер функций, расположенную на панели инструментов.
Введем Enter. На экране появится диалоговое окно Мастер функций — шаг 1 из 2.
В окне Категория выберите категорию Математические
В окне Функции выберите строку СУММПРОИЗВ. На экране появится диалоговое окно СУММПРОИЗВ (рис. 1.2.).
В строку Массив 1 введите В3: С3.
В строку Массив 2 введите В4: С4.

Рис. 1.2. Введены данные для функции СУММПРОИЗВ
Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а помещая курсор мыши в ячейки, чьи адреса следует ввести.
Массив 1 будет использоваться при вводе зависимостей для ограничений, поэтому на этот массив надо сделать абсолютную ссылку. В Excel можно использовать относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, и абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например $А$2, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при копировании, а абсолютные — нет.
4. Ввести зависимости для ограничений.
Содержимое ячейки D4 скопируем в ячейки D5—D7 (рис. 1.3.). Содержимое ячеек D4— D7 необходимо проверить. Они обязательно должны содержать информацию, как это показано для примера на рис. 1.4
Чтобы работать в режиме представления формул в Excel, необходимо выбрать меню Сервис, Параметры, в этом поле выбрать команду отображать формулы.)

Рис. 1.3. Введены зависимости для целевой функции и всех ограничений
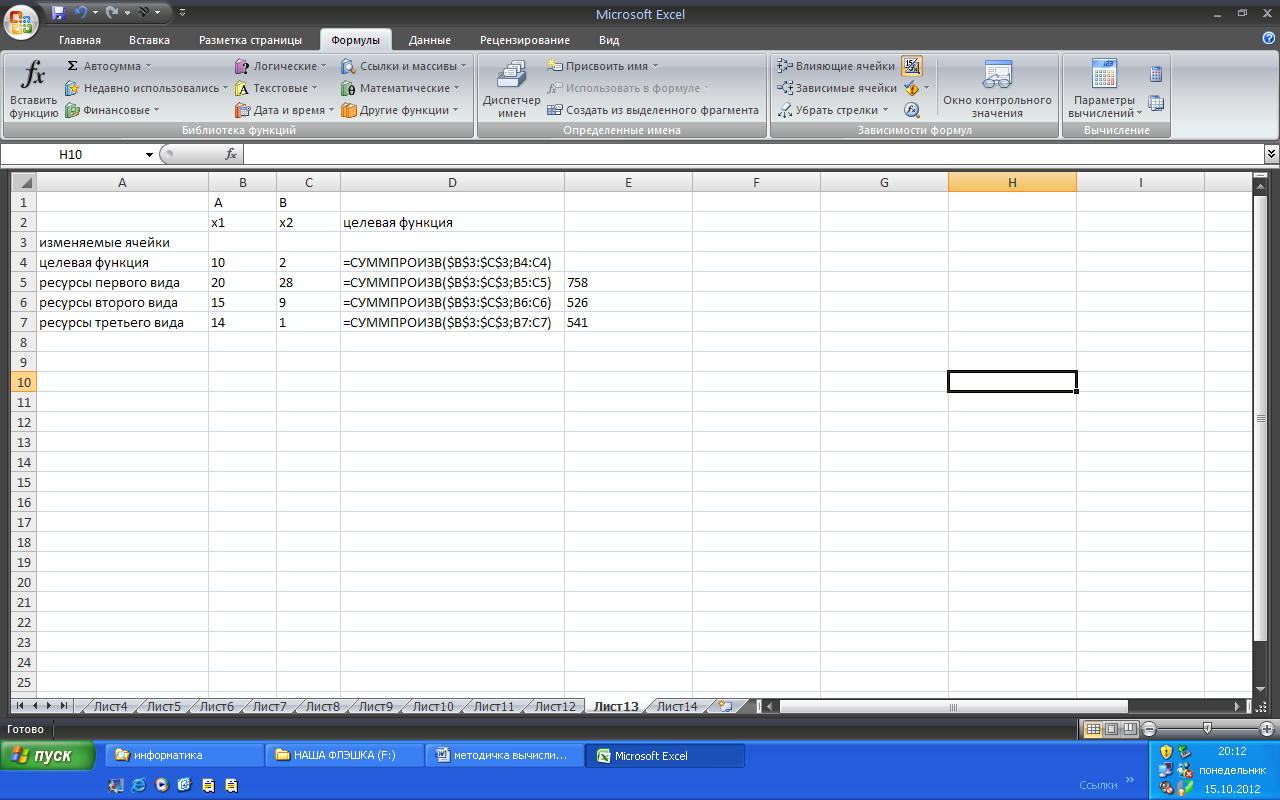
Рис. 1.4. Проверка содержимого ячеек D4— D7
5. Запускаем команду Поиск Решения.
В строке Меню указатель мыши поместите на Сервис.
В развернутом меню выберите команду Поиск решения. Появится диалоговое окно Поиск решения (рис. 1.5.).
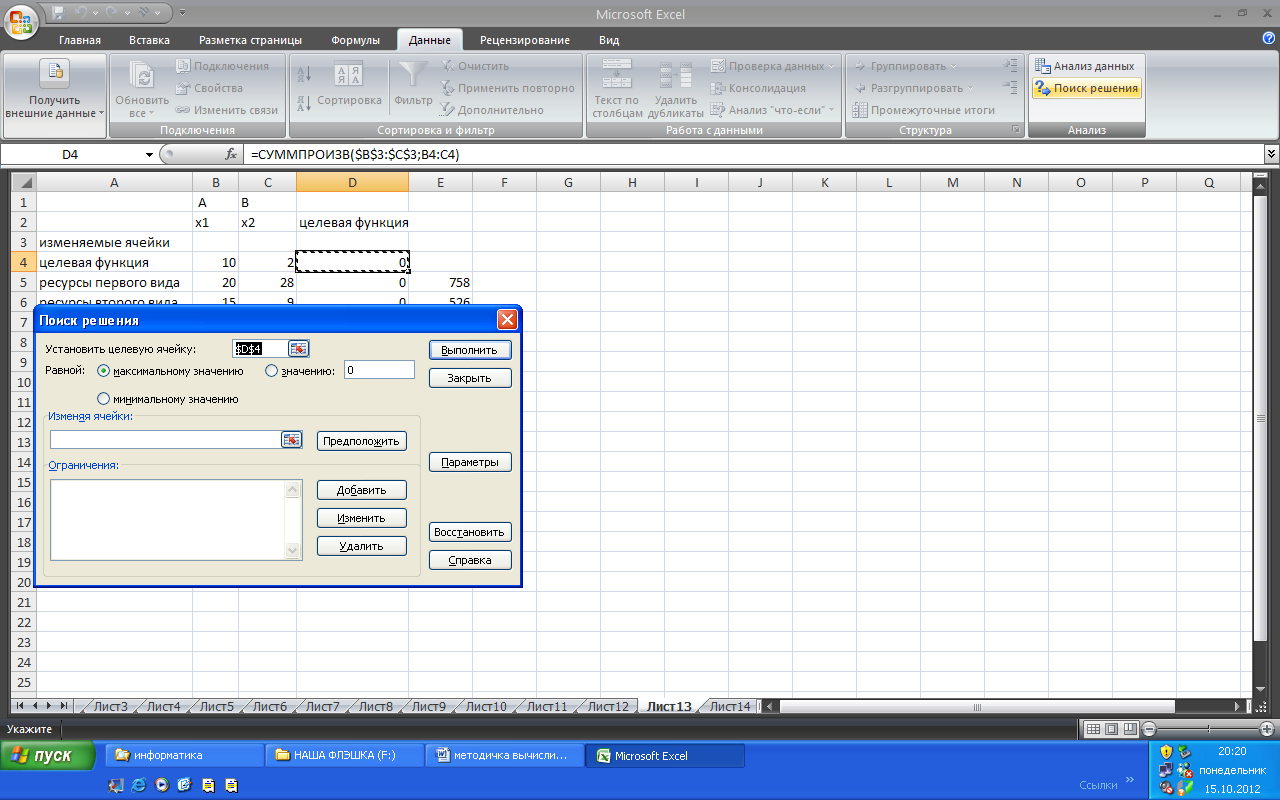
Рис. 1.5. Меню Поиск Решения.
6. Назначим ячейку для целевой функции.
Поясним смысл элементов окна Поиск решения на примере нашей задачи.
Установить целевую ячейку — определяет целевую ячейку, значение которой необходимо либо максимизировать, либо минимизировать, либо сделать равным конкретному значению.
· Помещаем курсор в строку Установить целевую ячейку.
Сюда необходимо внести адрес ячейки, содержащей целевую функцию.
· Введем адрес ячейки $D$4. Для того чтобы сделать это, нужно щелкнуть мышью на той ячейке рабочего листа, где содержится целевая функция, - D4. Вокруг D4 появится движущийся пунктирный контур, а в поле окна — соответствующий адрес.
· Введем тип целевой функции в зависимости от условия задачи. Для этого отметим, чему равна целевая функция — Максимальному значению или Минимальному значению.
Изменяя ячейки — определяет изменяемые ячейки. Изменяемая ячейка — это ячейка, которая может быть изменена в процессе поиска решения для достижения нужного результата. Допускается задание до 200 изменяемых ячеек.
· Поместим курсор в строку Изменяя ячейки.
· Введем адреса искомых переменных $В$3:$С$3.
ü Предположить — отыскивает все неформульные ячейки, прямо или непрямо зависящие от формулы в окне Установить целевую ячейку, и помещает их ссылки в окно Изменяя ячейки.
ü Ограничения — перечисляет текущие ограничения в данной задаче.
ü Добавить — выводит диалоговое окно Добавление ограничения, в котором можно добавить ограничения к текущей задаче.
ü Изменить — выводит диалоговое окно Изменение ограничения, в котором можно модифицировать имеющиеся ограничения.
ü Удалить — удаляет выделенное ограничение.
7. Введем ограничения.
· Поместим указатель мыши на кнопку Добавить. На экране появится диалоговое окно Добавление ограничения (рис.1. 6.).

Рис. 1.6. Диалоговое окно Добавление ограничения
Excel воспринимает ограничения в виде ссылок на ячейки, в которых содержатся соответствующие формулы, при этом левая часть ограничения представляет собой, как правило, ссылку на формулу, а правая — значение: число или ссылку на ячейку, содержащую значение. Адреса ячеек должны содержать символ $. Если определяется интервал ячеек, то он должен быть той же формы и тех же размеров, что и интервал в окне Ссылка на ячейку.
Поясним смысл элементов окна Добавление ограничения.
ü Ссылка на ячейку — определяет ячейку или интервал ячеек, чьи значения необходимо ограничить.
ü Ограничение — определяет условие, налагаемое на содержимое окна Ссылка на ячейку.
· В строке Ссылка на ячейку введем адрес диапазона ячеек $D$4: $D$7.
· Введем знак ограничения: выберем из списка отношение, которое нужно установить между ячейкой (или интервалом) и ограничением, которое нужно ввести в окне справа от списка.
Можно выбрать < =, =,> =, или «цел». Если вы выбрали «цел» для указания на то, что переменная должна быть целочисленной, то слово «Целое» появится в окне справа от списка.
· В строке Ограничение введем адрес $E$5: $E$7 (рис. 1.7).

Рис. 1.7. Добавлены ограничения
После того как введены все ограничения, нажмите кнопку ОК. На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 1.8.).

Рис. 1.8. Введены все условия задачи
8. Ввести параметры для решения задачи линейного программирования.
· В диалоговом окне Поиск решения поместите указатель мыши на кнопку Параметры. На экране появится диалоговое окно Параметры поиска решения (рис. 1.9).
С помощью команд, находящихся в этом окне, можно вводить условия для решения задач оптимизации всех классов. Можно определять параметры для линейных и нелинейных задач. Каждый из параметров в диалоговом окне имеет значение по умолчанию, подходящее для большинства задач.

Рис. 1.9. Введены параметры
Поясним смысл элементов окна Параметры поиска решения.
ü Максимальное время — служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах), не превышающее 32767; значение 100, используемое по умолчанию, подходит для большинства простых задач.
ü Предельное число итераций — ограничивает время, требующееся для процесса отыскания решения, путем ограничения числа итераций. Это значение должно быть положительным целым числом до 32 767.
ü Относительная погрешность — контролирует точность ответов, получаемых при поиске решений. Число, вводимое в это поле:
• используется при определении того, удовлетворяет ли значение ячейки Ограничение нужному равенству или находится ли оно в указанных границах;
• должно быть дробным числом от 0 до 1 (не включая концы);
• имеет значение по умолчанию, равное 0,000001;
• указывает на меньшую точность, если число введено с меньшим количеством десятичных знаков (например, 0,0001).
ü Допустимое отклонение —служит для задания величины отклонения от оптимального решения, если изменяемые ячейки ограничены множеством целых чисел. Чем выше отклонение (допустимое отклонение в процентах), тем быстрее процесс решения. Установка отклонения не играет роли, если не введены целочисленные ограничения.
ü Сходимость — применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Параметр принимает значения от 0 до 1. Лучшую сходимость характеризует большее количество десятичных знаков, например: 0,0001 соответствует меньшему относительному изменению по сравнению с 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения.
ü Линейная модель — ускоряет процесс отыскания решения. Команда может бьггь использована только, если все связи в модели линейны.
ü Показывать результаты итераций — прерывает поиск решения и показывает результаты после каждой итерации.
ü Автоматическое масштабирование — включает автоматический масштаб. Это полезно, когда параметры ввода (Изменяя яче£^ки) и вывода (Установить целевую ячейку и Ограничения) сильно различаются по величине; например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
ü Оценки — определяет подход, используемый для получения исходных оценок основных переменных в каждом одномерном поиске:
• линейная — использует линейную экстраполяцию вдоль касательного вектора;
• квадратичная — использует квадратичную экстраполяцию, что дает лучшие результаты для нелинейных задач.
ü Разности — определяет способ вычисления производной при оценке частных производных целевых и ограничивающих функций:
• прямые — такой способ дифференцирования установлен по умолчанию;
• центральные — требует больше вычислений на рабочем листе, но может помочь в тех случаях, когда получено сообщение о том, что Поиск решения не может улучшить решение.
ü Метод поиска — определяет, какой алгоритм используется при каждой итерации. Нужно указать один из методов:
• Ньютона — установлен по умолчанию. Обычно требует больше памяти, чем метод сопряженного градиента, но меньшее число итераций;
• сопряженного градиента — требует меньше памяти, чем метод Ньютона, но обычно большее число итераций для достижения конкретного уровня точности. Если объем вычислений достаточно велик и важно экономно использовать память, то целесообразно применять этот метод.
ü Загрузить модель — выводит окно диалога Загрузить модель, в котором можно указать, какую именно модель нужно загрузить.
ü Сохранить модель — выводит окно диалога Сохранить модель, в котором можно указать, где именно нужно сохранить данную модель. Используется кнопка Сохранить модель только в том случае, если нужно сохранить более чем одну модель Поиска решения вместе с данным рабочим листом. Первая модель Поиска решения автоматически сохраняется вместе с рабочим листом.
· Установим флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения.
· Поместим указатель мыши на кнопку ОК. На экране появится диалоговое окно Поиск решения.
· Поместите указатель мыши на кнопку Выполнить.
ü Выполнить — запускает процесс решения определенной задачи.
Через непродолжительное время появятся диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками ВЗ:СЗ для значений  и ячейкой D4 с максимальным значением целевой функции (рис. 1.10).
и ячейкой D4 с максимальным значением целевой функции (рис. 1.10).
Диалоговое окно Результаты поиска решения выводит результаты последнего вычисления, используя значения ячеек, наиболее близкие к нужному решению. Когда Поиск решения завершает попытки отыскания решения, то на экран вверху диалогового окна Результаты поиска решения выводится сообщение о завершении.

Рис. 1.10. Решение найдено
Поясним смысл элементов окна Результаты поиска решения.
ü Сохранить найденное решение — принимает решение, найденное Поиском решения, и подставляет найденные значения в соответствующие ячейки.
ü Восстановить исходные значения — восстанавливает исходные значения в изменяемых ячейках.
ü Тип отчета — создает указанный тип отчета. Каждый отчет появляется на отдельном листе рабочей книги.
• Результаты — перечисляет изменяемые ячейки и ячейку в окне Установить целевую ячейку вместе с исходным и конечным значением. Также показывает ограничения и информацию о них.
• Устойчивость — показывает, насколько чувствительно решение к изменениям коэффициентов в целевой функции или правых частей ограничений. Для нелинейных моделей отчет предоставляет двойственные значения (нормированные градиенты и множители Лагранжа), для линейных моделей — включает нормируемую стоимость, теневые цены и ограничения на изменение правой стороны равенства.
• Пределы — перечисляет изменяемые ячейки вместе с соответствующими значениями, ячейку в окне Установить целевую ячейку, верхние и нижние пределы и целевые значения. Нижний предел есть наименьшее значение, которое может находиться в изменяемой ячейке, если фиксировать остальные ячейки и удовлетворить все ограничения. Верхний предел есть наибольшее значение. Целевое значение есть значение ячейки в окне Установить целевую ячейку, когда значение изменяемой ячейки достигает наименьшего или наибольшего предела.
Если указать тип отчета Результаты, можно получить дополнительную информацию об оптимальном решении (рис. 1.11).
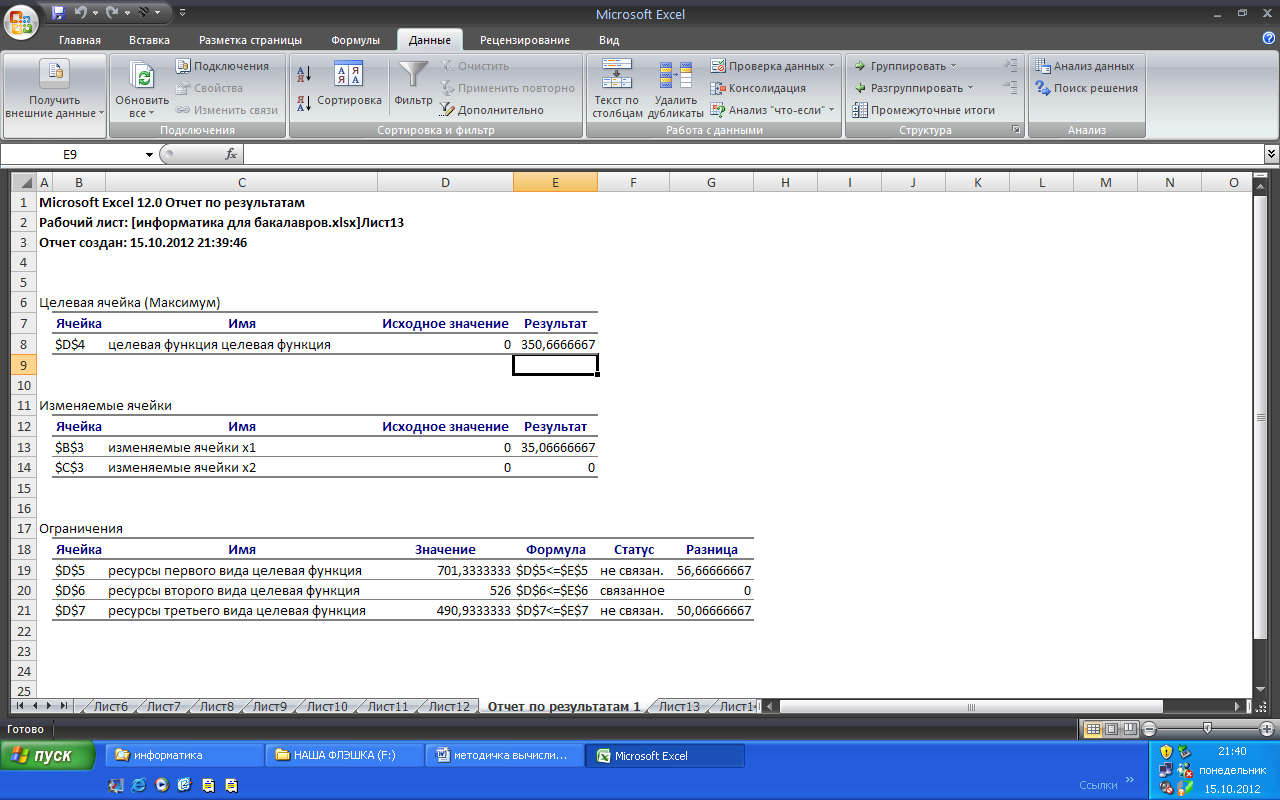
Риc.1. 11. Отчет Результаты
Ответ. Необходимо выпустить 35 изделий вида А, чтобы получить максимальную прибыль в 350 денежных единиц.
Особые случаи при решении ЗЛП в Excel:
1) получено сообщение Значения целевой ячейки не сходятся (рис. 1.12). Такое сообщение выдается в случае неограниченности целевой функции.
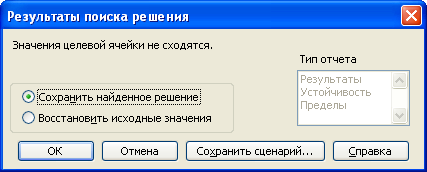
Рис. 1.12. Задача не имеет решения
2) получено сообщение Поиск не может найти подходящего решения (рис. 1.13). Такое сообщение выдается в случае несовместности системы ограничений.
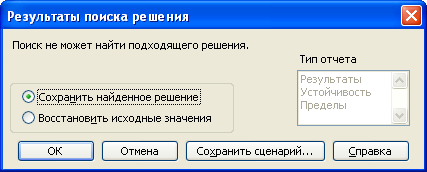
Рис. 1.13. Задача не имеет решения
1.3. Транспортная задача
Рассмотрим задача транспортировки продукта, который в определенных количествах предлагается различными производителями. Известны потребности нескольких потребителей в этом продукте. Требуется определить, от каких производителей и в каких объемах должны получать продукт потребители. Поставки должны осуществляться таким образом, чтобы совокупные издержки на транспортировку продукта были минимальными.
Обозначения:
 — величина предложения продукта в пункте i (i = 1,..., n);
— величина предложения продукта в пункте i (i = 1,..., n);
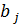 — величина спроса на продукт в пункте j (j = 1,..., т);
— величина спроса на продукт в пункте j (j = 1,..., т);
 — затраты на транспортировку единицы продукта из пункта i в пункт j;
— затраты на транспортировку единицы продукта из пункта i в пункт j;
 — количество продукта, перевозимого из пункта i в пункт j.
— количество продукта, перевозимого из пункта i в пункт j.
Модель транспортной задачи:
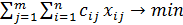 , (1.7)
, (1.7)
 ,
, 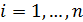 , (1.8)
, (1.8)
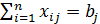 ,
,  , (1.9)
, (1.9)
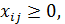
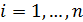 ;
;  . (1.10)
. (1.10)
Здесь (1.7) — целевая функция (минимум затрат на транспортировку продукта);
(1.8)— ограничения по величине предложения в каждом пункте производства;
(1.9)— ограничения по величине спроса в каждом пункте потребления;
(1.10)— условия неотрицательности объемов перевозок.
1. Замкнутая транспортная задача. Общее предложение равно общему спросу:

Это необходимое и достаточное условие существования допустимого плана задачи (1)—(4).



 (1.1)
(1.1)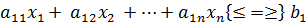 ,
, ,
, ;
; , j=
, j=  (1.3)
(1.3)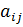 ,
,  ,
, 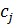
 - заданные постоянные величины.
- заданные постоянные величины. , удовлетворяющий ограничениям (2) и (3), называется допустимым решением (планом) задачи линейного программирования. План
, удовлетворяющий ограничениям (2) и (3), называется допустимым решением (планом) задачи линейного программирования. План  , при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным.
, при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным. (1.4)
(1.4) , j=
, j=  (1.5)
(1.5)
 (1.6)
(1.6) при следующей системе ограничений:
при следующей системе ограничений: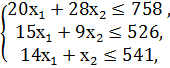


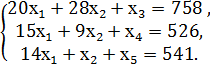

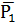 =
=  ;
;  =
=  ;
;  =
=  ;
; =
=  ;
;  =
= 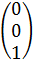 , координатами которых будут коэффициенты при неизвестных, взятые из левой части системы ограничений, и вектор
, координатами которых будут коэффициенты при неизвестных, взятые из левой части системы ограничений, и вектор  =
= 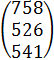 , координатами которого являются свободные члены системы ограничений.
, координатами которого являются свободные члены системы ограничений. - линейно- независимые векторы. Это допустимый базис задачи.
- линейно- независимые векторы. Это допустимый базис задачи.
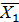 ={0,0,758,526,541}, т.е. свободные переменные
={0,0,758,526,541}, т.е. свободные переменные  ,
, 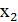 полагаем равными нулю, а базисные
полагаем равными нулю, а базисные  - координатам вектора
- координатам вектора 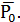
 = min{37,9;35,066;38,64}=35 то направляющей будет строка ().
= min{37,9;35,066;38,64}=35 то направляющей будет строка ().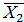 ={35,066, 0, 56,66, 0, 50,066}. Он является оптимальным, так в индексной строке нет отрицательных чисел. Zmax= 350,66
={35,066, 0, 56,66, 0, 50,066}. Он является оптимальным, так в индексной строке нет отрицательных чисел. Zmax= 350,66 , х 2число единиц продукции каждого вида. В нашей задаче оптимальные значения вектора
, х 2число единиц продукции каждого вида. В нашей задаче оптимальные значения вектора 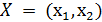 будут помещены в ячейках B3:C3, а оптимальное значение целевой функции - в ячейке D4.
будут помещены в ячейках B3:C3, а оптимальное значение целевой функции - в ячейке D4.








 и ячейкой D4 с максимальным значением целевой функции (рис. 1.10).
и ячейкой D4 с максимальным значением целевой функции (рис. 1.10).



 — величина предложения продукта в пункте i (i = 1,..., n);
— величина предложения продукта в пункте i (i = 1,..., n);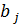 — величина спроса на продукт в пункте j (j = 1,..., т);
— величина спроса на продукт в пункте j (j = 1,..., т); — затраты на транспортировку единицы продукта из пункта i в пункт j;
— затраты на транспортировку единицы продукта из пункта i в пункт j; — количество продукта, перевозимого из пункта i в пункт j.
— количество продукта, перевозимого из пункта i в пункт j.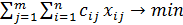 , (1.7)
, (1.7) ,
, 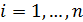 , (1.8)
, (1.8)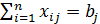 ,
,  , (1.9)
, (1.9)