Результаты работы могут быть использованы в теории квантовой информации и квантовых вычислений при выборе и определении оптимальных режимов работы логических элементов квантовых компьютеров в виде двухуровневых атомов или ионов в оптических и магнитных ловушках
Полученные в работе результаты могут также использоваться в учебном процессе при подготовке студентов, специализирующихся по теоретической физике, лазерной физике и оптике.
Структура и объем работы
Работа изложена на 34 страницах печатного текста. Состоит из введения, 3 глав, заключения и библиографический список, который включает 41 наименования. Общий объем работы 34 траниц текста.
Глава 1. Модель Джейнса-Каммингса. Кубит
Модель Джейнса-Каммингса
Модель Джейнса- Каммнгса была предложена в 1963 году Эдвином Джейнсом и Фредом Каммингсом при сравнении полуклассической теории спонтанного излучения и квантовой теории излучения. В полуклассической теории взаимодействия атом-поле, поле рассматривалось как функция времени, а не как оператор, атом же квантовался. Многие явления в современной оптике описываются полуклассической теорией (например, цикл Раби).
Модель Джейнса-Каммингса показала, что на эволюцию состояния двухуровневой системы влияет квантование поля излучения по сравнению с полуклассической теорией взаимодействия света и атомов. Так же было обнаружено, дискретность состояния поля влечет за собой распад и возрождение атомной инверсии. Такой чисто квантовый эффект может быть описан моделью Джейнса-Каммингса, но только в случае полуклассической теории. В 1987 году Ремпе, Вальтер, и Кляйн продемонстрировали случай квантовых коллапсов (распадов) и ревайвэлов (возрождений) в одноатомном мазере.
Рассмотрим модель Джейнса-Каммингса подробнее. Для данной системы можно записать гамильтониан с помощью гамильтониана из классической электродинамики. Нерелятивистский электрон взаимодействует с потенциальным полем U(r) и электромагнитным полем с потенциалом A(r). Классический гамильтониан для такой системы будет иметь вид:
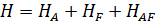 , (1.1)
, (1.1)
Каждое слагаемое распишем:
 .
.
здесь p-импульс электрона, m-его масса, e-заряд. 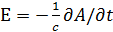 ,
,
 , электромагнитное поле поперечное. Член
, электромагнитное поле поперечное. Член  описывает возмущение, а
описывает возмущение, а 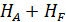 гамильтониан невозмущенной системы, в рамках теории возмущения.
гамильтониан невозмущенной системы, в рамках теории возмущения.
Само представление о двухуровневом атоме построено на предположении о том, что из всех возможных состояний мы можем ограничится лишь двумя, и ограничение накладывается так же моду поля, в данном случае рассматривается одна мода поля.
Состояние атома, как известно, ограничивается правилами отбора и характеризуется значениями момента и четности. В модели Джейнса-Каммингса всевозможные типы переходов, в частности дипольные переходы.
Задача сводится к вычислению члена  в выбранном базисе, но обычно этим членом пренебрегают, а более точное вычисление
в выбранном базисе, но обычно этим членом пренебрегают, а более точное вычисление  приводит к перенормировке массы.
приводит к перенормировке массы.
Запишем векторный потенциал в рамках вторичного квантования для одной моды поля:
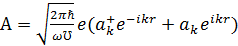 , (1.2)
, (1.2)
где e-единичный вектор поляризации,  - частота,
- частота,  -объем квантования.
-объем квантования.
Так как объемы атома намного меньше чем длина волны оптического излучения, то мы можем прибегнуть к следующему приближению: 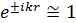 . Тогда для матричных элементов
. Тогда для матричных элементов  в данном приближении:
в данном приближении:
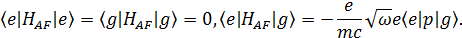
Беря в учет соотношение 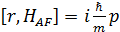 , заменим матричные элементы импульса на радиус-вектор. Так же введем атомные операторы
, заменим матричные элементы импульса на радиус-вектор. Так же введем атомные операторы
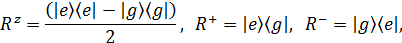
Тогда гамильтониан будет иметь вид:
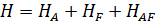 , (1.3)
, (1.3)
где 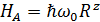 ,
, 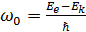 ,
, 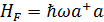 ,
, 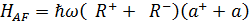 ,
,  .
.
Дальше нужно из  исключить члены
исключить члены 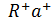 ,
, 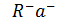 . В итоге мы приходим к модели Джейнса-Каммингса:
. В итоге мы приходим к модели Джейнса-Каммингса:
 . (1.4)
. (1.4)
Можно подчеркнуть, что аналогичный по структуре гамильтониан можно получить при приближении 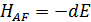 , подробнее этот вопрос можно рассмотреть в работе [16].
, подробнее этот вопрос можно рассмотреть в работе [16].
Кубит
Квантово-механические процессы, как правило, описываются переходами между энергетическими уровнями [37]. Один из уровней описывает начальное состояние до перехода, второй уровень-конечное состояние после перехода. Нужно отметить, что такой переход так же может осуществляться через несколько промежуточных состояний.
Существует система, называемая кубитом, в которой можно ограничится рассмотрением двух уровней.
Применим постулаты квантовой механики к описанию кубита. Пространство состояний кубита является двумерным гильбертовым пространством. Вектор произвольного состояния кубита есть когерентная линейная суперпозиция базисных состояний:
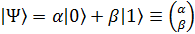 , (2.1)
, (2.1)
где 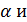
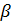 - комплексные числа, удовлетворяющие условию нормировки:
- комплексные числа, удовлетворяющие условию нормировки:  ; векторы
; векторы 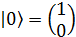 и
и 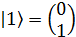 – ортонормированные базисные состояния. При этом положении кубит находится в обоих состояниях одновременно. Базисные состояния кубита могут быть выбраны произвольным образом, различается лишь поворот в двухмерном базисном состоянии. Выбор базиса определяется измерительным процессом.
– ортонормированные базисные состояния. При этом положении кубит находится в обоих состояниях одновременно. Базисные состояния кубита могут быть выбраны произвольным образом, различается лишь поворот в двухмерном базисном состоянии. Выбор базиса определяется измерительным процессом.
С помощью вектора состояния 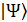 описывается «чистое» состояние, состояние замкнутой квантовой системы. На самом деле данная система рассматривается в совокупности квантовой системы, которая взаимодействует с окружением (Рисунок 1).
описывается «чистое» состояние, состояние замкнутой квантовой системы. На самом деле данная система рассматривается в совокупности квантовой системы, которая взаимодействует с окружением (Рисунок 1).

Рис. 1. Смешанное состояние  ,являющаяся частью системы.
,являющаяся частью системы.
Чтобы описать отельные подсистемы нужно пользоваться матрицей плотности 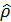 . Опишем систему, состояние которой нам не полностью известно, для этого воспользуемся понятием статистического ансамбля чистых состояний, вероятность нахождения системы в них равна
. Опишем систему, состояние которой нам не полностью известно, для этого воспользуемся понятием статистического ансамбля чистых состояний, вероятность нахождения системы в них равна 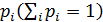 . Таким состоянием системы называют смешанное состояние.
. Таким состоянием системы называют смешанное состояние.



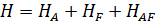 , (1.1)
, (1.1) .
.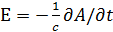 ,
, , электромагнитное поле поперечное. Член
, электромагнитное поле поперечное. Член  описывает возмущение, а
описывает возмущение, а 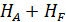 гамильтониан невозмущенной системы, в рамках теории возмущения.
гамильтониан невозмущенной системы, в рамках теории возмущения. приводит к перенормировке массы.
приводит к перенормировке массы.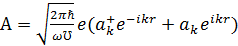 , (1.2)
, (1.2) - частота,
- частота,  -объем квантования.
-объем квантования.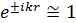 . Тогда для матричных элементов
. Тогда для матричных элементов 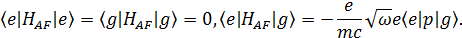
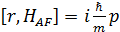 , заменим матричные элементы импульса на радиус-вектор. Так же введем атомные операторы
, заменим матричные элементы импульса на радиус-вектор. Так же введем атомные операторы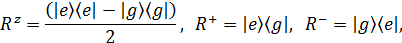
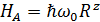 ,
, 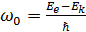 ,
, 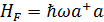 ,
, 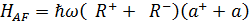 ,
,  .
.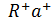 ,
, 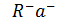 . В итоге мы приходим к модели Джейнса-Каммингса:
. В итоге мы приходим к модели Джейнса-Каммингса: . (1.4)
. (1.4)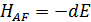 , подробнее этот вопрос можно рассмотреть в работе [16].
, подробнее этот вопрос можно рассмотреть в работе [16].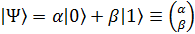 , (2.1)
, (2.1)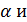
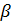 - комплексные числа, удовлетворяющие условию нормировки:
- комплексные числа, удовлетворяющие условию нормировки:  ; векторы
; векторы 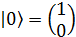 и
и 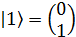 – ортонормированные базисные состояния. При этом положении кубит находится в обоих состояниях одновременно. Базисные состояния кубита могут быть выбраны произвольным образом, различается лишь поворот в двухмерном базисном состоянии. Выбор базиса определяется измерительным процессом.
– ортонормированные базисные состояния. При этом положении кубит находится в обоих состояниях одновременно. Базисные состояния кубита могут быть выбраны произвольным образом, различается лишь поворот в двухмерном базисном состоянии. Выбор базиса определяется измерительным процессом.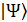 описывается «чистое» состояние, состояние замкнутой квантовой системы. На самом деле данная система рассматривается в совокупности квантовой системы, которая взаимодействует с окружением (Рисунок 1).
описывается «чистое» состояние, состояние замкнутой квантовой системы. На самом деле данная система рассматривается в совокупности квантовой системы, которая взаимодействует с окружением (Рисунок 1).
 ,являющаяся частью системы.
,являющаяся частью системы.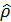 . Опишем систему, состояние которой нам не полностью известно, для этого воспользуемся понятием статистического ансамбля чистых состояний, вероятность нахождения системы в них равна
. Опишем систему, состояние которой нам не полностью известно, для этого воспользуемся понятием статистического ансамбля чистых состояний, вероятность нахождения системы в них равна 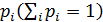 . Таким состоянием системы называют смешанное состояние.
. Таким состоянием системы называют смешанное состояние.


