Соотношения электростатики
Характер отклика материала на воздействие приложенного электрического поля легче всего представить на примере плоского конденсатора [4]. Пусть постоянная разность потенциалов V приложена к пластинам такого конденсатора c площадью металлических пластин (обкладок) S, находящимся на расстоянии d в вакууме (рис. 1.1а). Пренебрегая краевыми эффектами, можно считать, что электрическое поле Е в промежутке между пластинами будет однородным:
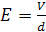 (1.1)
(1.1)
Следует заметить, что электрическое поле имеет не только величину, но и направление, поэтому более полно характеризуется векторной величиной, обозначаемой Е и имеющей компоненты Ex, Ey, Ez. В рассматриваемом случае поле должно быть направлено перпендикулярно пластинам. В системе СИ фундаментальный закон Кулона связывает силу F, действующую между двумя точечными зарядами q1 и q2, находящимися в вакууме и расстояние r: F =q1q2 r /(4πεor3), где коэффициент пропорциональности εo называется диэлектрической проницаемостью вакуума и равен 8,85•10–12 Ф•м–1. Появление множителя 4π в знаменателе связано с тем, что диэлектрическая проницаемость (как и магнитная) нормирована, с тем, чтобы избежать постоянного присутствия этого множителя в уравнениях Максвелла.
Из закона Кулона следует, что плотность зарядов (+Q) и (–Q) на пластинах (чаще плотность зарядов Q/S обозначается как σ [Kл/м2]) прямо пропорциональна величине поля, т.е.
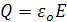 (1.2)
(1.2)
Емкость конденсатора в вакууме Со на единицу площади электрода равна отношению плотности заряда к приложенному напряжению
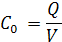 (1.3)
(1.3)
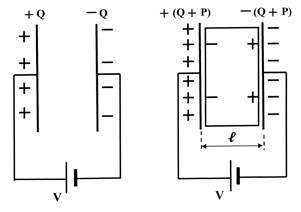
Рис. 1.1. Заряды на пластинах плоского конденсатора в случае, когда между пластинами находится вакуум (а) и диэлектрик (б)
Рассмотрим теперь конденсатор, в котором между пластинами находится интересующий нас диэлектрик той же площади S (рис. 1.1б). Под действием приложенного электрического поля заряды в диэлектрическом материале (электроны и протоны) перераспределяются, поскольку положительные заряды притягиваются к отрицательному электроду и наоборот. Это явление называется поляризацией материала. Если материал изотропен, влияние электрического поля сведется к появлению в каждом элементарном объеме dv малого дипольного момента Р dv, ориентированного параллельно полю. Поляризация Р, таким образом, определяется как векторная величина, выражающая величину и направление электрического момента, наведенного в материале внешним полем. Каждый элемент объема поляризованного материала электрически подобен двум зарядам +q и –q, находящимся на расстоянии ℓ в направлении поля, и обладает дипольным моментом Q ℓ = P dv. Эти диполи складываются как стопка магнитиков, и на поверхностях, прилегающих к электродам, появляются заряды с плотностью +Р и Р [1, 2, 9]. Используя теорему Грина, можно строго показать, что поле, обусловленное однородной поляризацией Р в материале, эквивалентно полю, возникающему при наличии заряда Рn, распределенного на граничной поверхности, где Рn нормальная компонента поляризации на поверхности. Вектора Е и Р при этом сонаправлены. Дипольный момент направлен от –q к +q. Наличие поляризации, или связанных зарядов, означает, что на электродах конденсатора может быть запасен больший заряд и, таким образом, емкость системы возрастает. Отношение этой емкости к емкости в вакууме зависит от материала и определяется величиной
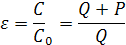 (1.4)
(1.4)
наведенной в нем поляризации.
Это отношение не зависит от приложенного напряжения и, следовательно, от величины электрического поля и называется диэлектрической постоянной материала. Подставляя Q из уравнения (1.2) в уравнение (1.4) и используя векторные обозначения, получаем
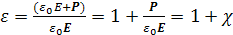 (1.5)
(1.5)
где 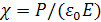 электрическая восприимчивость материала.
электрическая восприимчивость материала.
Величина εεo Е, называемая электрическим смещением D в материале, получается преобразованием уравнения (1.5):
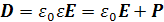 (1.6)
(1.6)
Это основное уравнение электрического поля, которое выполняется в любой точке изотропной среды. Величина εεo является абсолютной диэлектрической проницаемостью материала, а отношение ε, названное нами выше диэлектрической постоянной материала, более точно следует называть относительной диэлектрической проницаемостью (по отношению к абсолютной диэлектрической проницаемости вакуума εo); в дальнейшем этот термин и будет использоваться. Поток электрического смещения начинается и заканчивается на свободных зарядах, будучи непрерывным даже на границе двух сред. Электрическое поле, напротив, испытывает разрыв на границе двух материалов из–за различия в них величины поляризации.
Рассматривая поляризацию на молекулярном уровне, можно сказать, что влияние внешнего электрического поля заключается в индуцировании электрического заряда.
Когда поле невелико, величина поляризации прямо пропорциональна величине поля. В случае анизотропного материала ее направление не обязательно совпадает с направлением поля диполя m на каждой отдельной молекуле, величина которого зависит от локальной напряженности электрического поля E L:
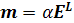 (1.7)
(1.7)
Коэффициент пропорциональности, а называется поляризуемостью молекулы. Для изотропных молекул, в том числе одноатомных молекул инертных газов, направление индуцированных диполей в среднем совпадает с направлением внешнего поля. (Поскольку локальное поле, как мы увидим в дальнейшем, пропорционально полному внешнему полю, m = const • Е.) Полный дипольный момент единицы объема, поляризация Р, зависит от числа молекул в единице объема N o:
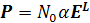 (1.8)
(1.8)
В большинстве случаев молекулы анизотропные и их поляризуемость зависит от направления внешнего поля, так что направление индуцированного диполя не совпадает с направлением внешнего поля. Говоря более строго, поляризуемость является симметричным тензором второго ранга, связывающим вектор индуцированного диполя с вектором внешнего поля:
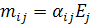 (1.9)
(1.9)
с основными компонентами α1, α2 и α3 в приведении к главным осям:
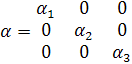 (1.10)
(1.10)
Тогда ε может рассматриваться как скалярная величина, не зависящая от направления вектора электрического поля, как в уравнении (1.6). Это утверждение теряет силу, если в диэлектрике имеется выделенное направление вследствие, например, механической деформации или твердотельной полимеризации. В этом случае относительная диэлектрическая проницаемость оказывается тензором έ:
D =εoέ E (1.11)
Число компонентов тензора относительной диэлектрической проницаемости уменьшается при появлении симметрии в материале. В продольно ориентированном материале имеются две независимые компоненты, параллельная и перпендикулярная направлению ориентации (ε║ и ε┴ или ε1 и ε2), поскольку материал изотропен в плоскости, нормальной направлению ориентации, т.е. ε1 = ε2.
Приведенное выше рассмотрение справедливо для линейного диэлектрика, в котором поляризация пропорциональна величине внешнего поля. В реальности, как и для большинства физических явлений, диэлектрические свойства материалов нелинейные. К счастью, коэффициенты при членах более высоких порядков, Е 2, Е 3 и т.д., малы и ими обычно можно пренебречь. Однако в некоторых условиях они становятся, как мы увидим в дальнейшем, заметны.
Молекулярная поляризуемость
Рассмотрим теперь более детально поляризацию на молекулярном или микроскопическом уровне. Молекулярная поляризация имеет три составляющие [4].
1. Электронная поляризация. В любом атоме электрическое поле вызывает смещение электронов относительно положительно заряженного ядра. Это смещение незначительно, поскольку величина внешнего поля обычно намного меньше воздействия, оказываемого на электрон ядром атома. Так, принимая заряд протона равным 1,6•10–19 Кл, а типичный радиус атома 10–10 м, получим, что напряженность электрического поля в точке, где находится электрон, составляет 1011 В•м–1, тогда как внешние поля редко превышают 108 В•м–1. При этом электронная поляризация проявляется на очень высоких частотах и ответственна за преломление света.
Электронная поляризация сферического атома может быть рассчитана исходя из нескольких приближенных моделей. В первой из известных моделей атом рассматривался как проводящая сфера радиусом R; тогда можно показать, что поляризуемость равна 4πεоR3 величине, приблизительно равной объему молекулы. Используя более реалистичную полуклассическую модель атома Бора, можно показать, что воздействие внешнего поля, направленного по нормали к плоскости орбиты электрона радиусом R, вызовет ее небольшой сдвиг – х, как показано на рис. 1.2. В первом приближении радиус орбиты останется неизменным и равным R, а индуцированный дипольный момент μ, атома будет равен e•x. При этом внешнее поле, действующее на электрон, уравновешивается кулоновским полем положительно заряженного ядра:
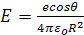 (1.12)
(1.12)
где cosθ≈ x/R. Тогда электронная поляризуемость атома:
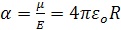 3 (1.13)
3 (1.13)
Более точные квантовомеханические расчеты отличаются от этого выражения множителем 9/2.
Возникновение анизотропии электронной поляризации в молекулах можно проследить на примере простой двухатомной молекулы, состоящей из двух одинаковых атомов радиусом R, находящихся на расстоянии L во внешнем электрическом поле Е.
На каждый атом воздействует внешнее поле и поле диполя, наведенного в соседнем атоме. Если поля параллельны (рис. 1.3а), они складываются и диполь μ║, наведенный в каждом атоме с поляризуемостью α, определяется уравнением
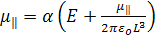 (1.14)
(1.14)
Решая уравнение относительно μ║, получаем
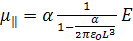 (1.15)
(1.15)
соответственно, поляризуемость α║ всей молекулы равна
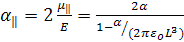 (1.16)
(1.16)
При поперечной ориентации (рис. 1.3б) поле наведенного диполя на соседнем атоме направлено противоположно внешнему полю и наведенный диполь определяется
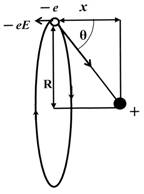
Рис. 1.2. Наведенный диполь при смещении орбиты электрона в атоме [10, 11]
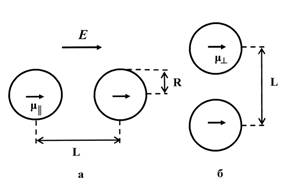
Рис. 1.3. Поляризуемость двухатомной молекулы: а) в направлении внешнего поля и б) в поперечном направлении
уравнением
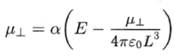 (1.17)
(1.17)
Поперечная поляризуемость молекулы равна
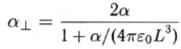 (1.18)
(1.18)
Если поляризуемость каждого атома 4πεоR3, получаем
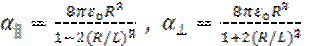 (1.19)
(1.19)
Таким образом, в первом приближении получаем выражение для степени анизотропии (α║ – α┴) [4]:
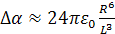 или
или 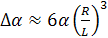 (1.20)
(1.20)
2. Атомная поляризация. Внешнее электрическое поле может приводить к смещению ядер атомов в молекуле или в кристаллической решетке. Тяжелые ядра атомов менее подвижны, чем электроны, и поляризация атомов не может иметь места на столь же высоких частотах, что и электронная поляризация, а потому она наблюдается при частотах не выше ИК диапазона. Из данных колебательной спектроскопии известно, что в молекулярных твердых телах силовые постоянные для изгибных и крутильных колебаний, при которых изменяются углы связей, обычно намного меньше силовых постоянных для валентных (растягивающих) колебаний. Поэтому можно ожидать, что изгибные моды вносят основной вклад в атомную поляризацию. Величина атомной поляризации обычно мала и составляет всего одну десятую от электронной поляризации, хотя и существуют исключения, когда одна из изгибных мод приводит к значительному отклонению от симметричного расположения центров положительных и отрицательных зарядов в молекуле. В ионных соединениях этот эффект может быть достаточно велик, например в случае кристалла хлорида натрия при сдвиге всех положительных ионов относительно отрицательных [4].
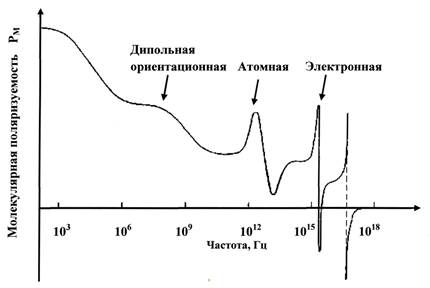
Рис. 1.4. Дисперсия молекулярной поляризации в диэлектрике [12]
3. Ориентационная поляризация. В случае, когда молекулы обладают собственным постоянным дипольным моментом, они ориентируются во внешнем поле, вследствие чего возникает поляризация в этом направлении. Это явление обсуждается в следующем параграфе, а скорость ориентации диполей, сильно зависящая от межмолекулярных взаимодействий, является предметом следующей главы. На данном этапе достаточно сказать, что ориентация молекулярных диполей может вносить значительный вклад в полную поляризацию материала во внешнем поле, однако быть достаточно медленной, чтобы проявиться полностью [4].
На рис. 1.4 показано характерное уменьшение поляризации материала с ростом частоты измерения, когда исчезает вклад менее компонентов молекулярной поляризации. Аналогичное поведение имеет место и для относительной диэлектрической проницаемости [4].
Локальное поле
Рассматривая диэлектрический материал на молекулярном уровне, мы начинаем сознавать, что электрическое поле внутри него меняется от точки к точке вследствие взаимодействия полей диполей, наведенных на каждой из молекул внешним полем. Хотя электрическое поле, усредненное по объему, достаточно большому по сравнению с размерами молекул (что эквивалентно электрическому полю в классической континуальной модели [8]), может быть однородным. Поле, действующее на отдельный поляризуемый объект, атом или молекулу, называется локальным полем EL и является важным понятием, связывающим наблюдаемое поведение материала как целого со свойствами составляющих его атомов или молекул.
При расчете локального поля удобно разделить его на две основные компоненты:
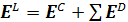 (1.21)
(1.21)
где Е С – поле, обусловленное зарядами на электродах, благодаря которым внешнее поле существует в материале, и ∑ Е D – сумма полей всех молекулярных диполей, за исключением диполя молекулы, находящейся в рассматриваемой точке образца. Решение в общем виде затруднено, поскольку для бесконечно большого образца сумма ∑ Е D не сходится, а также зависит от формы образца. Подход, впервые использованный Лоренцом и сыгравший важную роль в развитии теории диэлектриков, основан на следующей простой модели. Рассмотрим образец материала, помещенный между электродами плоского конденсатора, как показано на рис. 1.5, и сферу вокруг некоторой молекулы с центром в точке А. Локальное поле в точке А запишется в виде
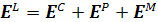 , ( 1.22)
, ( 1.22)
где сумма ∑ Е D разделена на составляющие ЕР – от части образца, лежащей вне сферы, и ЕМ – от образца внутри сферы. Если радиус сферы мал по сравнению с размером конденсатора, но велик в сравнении с молекулой, допустимо рассчитывать ЕР в рамках классической электростатики, рассматривая материал вне сферы как сплошную среду с диэлектрической проницаемостью ε. Дискретную структуру материала необходимо учитывать лишь при вычислении ЕМ. Рассмотрим теперь компоненты локального поля в отдельности.
Плотность заряда на электродах, как показано ранее, равна (Q + Р), поэтому величина поля за счет этого источника запишется в виде
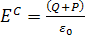 . (1.23)
. (1.23)
Подставляя Q из уравнения (1.2), получаем
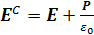 , (1.24)
, (1.24)
где Е внешнее поле (Е = V/d).
Поле в точке А от поляризации материала вне сферы в свою очередь можно разделить на две части, обусловленные кажущимися поверхностными зарядами, индуцированными этим полем на границах области. Первая часть обусловлена кажущимися зарядами с плотностью – Р и + Р на поверхности электродов и равна Р/εо. Вторая часть обусловлена кажущимися зарядами с плотностью Pcosθ на поверхности рассматриваемой сферы, где θ – угол, показанный на рис. 1.5, и может быть получена интегрированием по элементам поверхности между углами θ и (θ + dθ). Площадь такого элемента равна 2πr2sinθdθ.
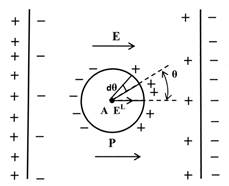
Рис. 1.5. Модель Лоренца для локального поля
По соображениям симметрии поля, перпендикулярные Р в центре сферы, взаимно уничтожаются и полное поле в направлении Р становится равным
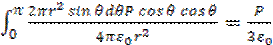 . (1.25)
. (1.25)
Отсюда имеем
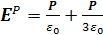 (1.26)
(1.26)
EM –поле в точке А от молекул внутри сферы, это поле зависит от конкретного их расположения. Для некоторых специальных случаев, например кубических решеток и полностью случайного распределения,
EM= 0. (1.27)
В этих случаях окончательно имеем для локального поля в точке А:
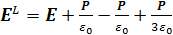 , (1.28)
, (1.28)
т. е. EL = E + P /3εo.
Подставляя Р из уравнения (1.5), получаем [4]
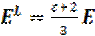 . ( 1.29)
. ( 1.29)





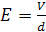 (1.1)
(1.1)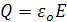 (1.2)
(1.2)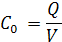 (1.3)
(1.3)
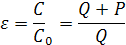 (1.4)
(1.4)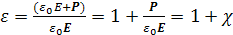 (1.5)
(1.5)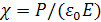 электрическая восприимчивость материала.
электрическая восприимчивость материала.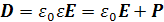 (1.6)
(1.6)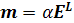 (1.7)
(1.7)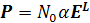 (1.8)
(1.8)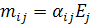 (1.9)
(1.9)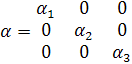 (1.10)
(1.10)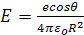 (1.12)
(1.12)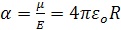 3 (1.13)
3 (1.13)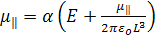 (1.14)
(1.14)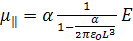 (1.15)
(1.15)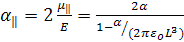 (1.16)
(1.16)

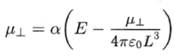 (1.17)
(1.17)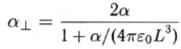 (1.18)
(1.18)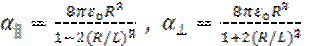 (1.19)
(1.19)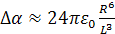 или
или 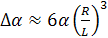 (1.20)
(1.20)
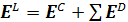 (1.21)
(1.21)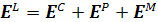 , ( 1.22)
, ( 1.22)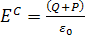 . (1.23)
. (1.23)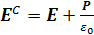 , (1.24)
, (1.24)
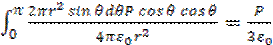 . (1.25)
. (1.25)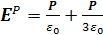 (1.26)
(1.26)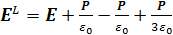 , (1.28)
, (1.28)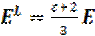 . ( 1.29)
. ( 1.29)

