В качестве переносчика информации s (t), излучаемого РПУ и называемого излучаемым сигналом, используется высокочастотное колебание
 (2.10.1)
(2.10.1)
представляющее собой детерминированную функцию. Огибающая колебания  , в общем случае комплексная, и несущая частота f 0 в значительной степени определяют качественные показатели системы и подлежат обоснованному выбору.
, в общем случае комплексная, и несущая частота f 0 в значительной степени определяют качественные показатели системы и подлежат обоснованному выбору.
Рассмотрим пример наложения информации на излучаемый сигнал s (t) в радиолокационных системах. На рис.2.19 изображен простейший радиолокационный сигнал, имеющий вид одиночного радиоимпульса с вещественной огибающей A (t) длительности t и (простой радиоимпульс)
 (2.10.2)
(2.10.2)

Рис 2.19
Сигнал (2), излученный радиолокационной станцией (РЛС), распространяется в сторону объекта (цели), координаты которого измеряются, отражается от объекта и возвращается к РЛС. Отраженный сигнал, принимаемый РЛС, обозначим s пр(t). Он отличается от излученного сигнала s (t), во-первых, запаздыванием по времени (рис.2.19), которое равно времени распространения электромагнитной волны от РЛС до цели и обратно
 , (2.10.3)
, (2.10.3)
где R - расстояние от РЛС до цели, c - скорость распространения радиоволн. Кроме того, при распространении и отражении сигнала происходит непредсказуемое уменьшение амплитуды импульса, которое характеризуют параметром интенсивности e, и также непредсказуемое изменение  начальной фазы сигнала при отражении. Поэтому принимаемый сигнал
начальной фазы сигнала при отражении. Поэтому принимаемый сигнал
 (2.10.4)
(2.10.4)
Обозначим сумму всех постоянных фазовых сдвигов, входящих в (4), символом j
 . (2.10.5)
. (2.10.5)
Начальная фаза является случайной величиной, которую обычно можно считать равномерно распределенной в интервале j Î(0, 2 p). В результате принимаемый сигнал
 (2.10.6)
(2.10.6)
имеет вид известной детерминированной функции времени t и совокупности неизвестных параметров t, j, e.
Рассмотрим более общий случай принимаемого сигнала короткого, но произвольного вида (1) с учетом того, что цель перемещается и дальность до цели в процессе ее облучения изменяется R = R (t). Положим t 0– средний момент облучения цели. Тогда на небольшом интервале облучения, равном длительности отраженного сигнала T с,
 , (2.10.7)
, (2.10.7)
где R (t 0) - дальность и 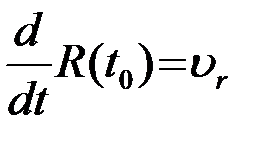 - радиальная скорость цели в момент t 0. Время запаздывания t (t) равно 2 R (t)/ c
- радиальная скорость цели в момент t 0. Время запаздывания t (t) равно 2 R (t)/ c
 ,
,
и 
Обозначим доплеровское смещение частоты
 ,
,
а сумму всех постоянных фазовых сдвигов j
 .
.
Кроме того, учтем что для узкополосных радиосигналов третьим слагаемым в аргументе комплексной огибающей  можно пренебречь. Условие, оправдывающее эту возможность и называемое условием узкополосности сигнала, сводится к следующему. Если на верхней частоте F с спектра огибающей
можно пренебречь. Условие, оправдывающее эту возможность и называемое условием узкополосности сигнала, сводится к следующему. Если на верхней частоте F с спектра огибающей  сдвиг фазы, обусловленный третьим слагаемым, мал
сдвиг фазы, обусловленный третьим слагаемым, мал
 , (2.10.8)
, (2.10.8)
то это слагаемое может быть опущено. Окончательно получаем
 (2.10.9)
(2.10.9)
Таким образом, в сигналах измерительного типа информация о дальности кодируется во временном запаздывании огибающей принимаемого сигнала относительно излученного, а информация о cкорости - в смещении несущей частоты сигнала. Другие параметры отражающих объектов и окружающей среды также проявляются в изменении некоторых параметров излучаемого (зондирующего) сигнала s (t). Обобщая рассмотрение, можно сделать вывод. Принимаемый сигнал измерительного типа так же, как и сигнал связного типа (дискретный и цифровой), имеет вид известной детерминированной функции времени t и ряда параметров l 1, l 1,..., lℓ, имеющих непредсказуемые значения. Один l 1 или несколько l 1,..., lk из этих параметров являются информационными и подлежат измерению в процессе обработки принимаемого колебания в РПрУ. Остальные параметры lk +1,..., lℓ сигнала  не несут полезной информации, называются несущественными и не подлежат измерению. В приведенном примере радиолокационного сигнала такими параметрами являются параметр интенсивности e и начальная фаза j.
не несут полезной информации, называются несущественными и не подлежат измерению. В приведенном примере радиолокационного сигнала такими параметрами являются параметр интенсивности e и начальная фаза j.
Излучаемый сигнал (1) обычно представляет собой не одиночный импульс, как это было принято в упрощенном примере (2) и показано на рис.2.19, а периодическую (с периодом T 0) последовательность лементарных импульсов
 (2.10.10)
(2.10.10)
При этом отраженный от цели принимаемый сигнал  вследствие движения цели и сканирования (перемещения) луча антенны РЛС имеет вид “пачки” импульсов
вследствие движения цели и сканирования (перемещения) луча антенны РЛС имеет вид “пачки” импульсов  конечной длительности T с. Модели пачек отраженных импульсов будут подробнее рассмотрены в §5.5.
конечной длительности T с. Модели пачек отраженных импульсов будут подробнее рассмотрены в §5.5.
СЛУЧАЙНЫЕ МОДЕЛИ СИГНАЛОВ
Общие сведения
Моделями случайных сигналов служат случайные функции времени - случайные процессы (СП). В § 2.1. уже было введено определение СП. Под СП понимается такая функция времени X(t), которая, являясь исходом случайного эксперимента, непредсказуемым образом принимает вид конкретной функции x(t,w) из некоторого множества функций {x(t,w), wÎW}, где Wмножество исходов случайного эксперимента. Каждому элементу w пространства исходов Wставится в соответствие конкретная реализация СП x(t,w), называемая также выборочной функцией или траекторией СП. Важно, что исходы СП не только непредсказуемы, но и обладают статистической устойчивостью. Последнее означает, что каждой реализации (исходу) можно приписать вероятностную меру, например, вероятность или плотность вероятностей. Полное задание СП предусматривает определение множества возможных реализаций {x(t,w), wÎW} и вероятностной меры, характеризующей вероятность появления отдельных реализаций.
На рис.3.1. ситуация иллюстрируется на упрощенном примере, в котором множество исходов состоит всего лишь из 3 элементов: w1=1, w2=2, w3=3. Им соответствуют три реализации - выборочные функции x(t,1), x(t,2), x(t,3), показанные на рисунке. Определены вероятности исходов P1, P2, P3 (P1+P2+P3 =1). Характерно, что отдельные реализации СП являются детерминированными функциями, заданными в данном случае графически. Возможность полного задания СП, приведенная в примере, не характерна для СП. Обычно множество исходов W бесконечное и нужен специальный математический аппарат для представления и анализа СП.

Рис. 3.1
В большинстве случаев для задания СП X(t) пользуются многомерными плотностями вероятностей (ПВ). Тождественным является подход, в котором пользуются многомерными функциями распределения. Сечение (отсчет, мгновенное значение) СП X(t) в некоторый фиксированный момент времени t1 представляет случайную величину X(t1)=X1. Так, например, для СП, представленного на рис.3.1., это случайная величина X1, принимающая одно из трех значений x(t1,1), x(t1,2), x(t1,3) с вероятностями соответственно P1, P2, P3. В общем случае сечение СП X(t1) - случайная величина X1, которая может принимать счетное или континуальное множество значений. Аналогично могут быть определены сечения СП в другие моменты времени t2,...,tn. При этом получаются случайные величины X(t2)=X2,...,X(tn)=Xn.
Плотность вероятности n-го порядка (n-мерная ПВ) СП X(t) называется совместная ПВ n случайных величин X1,.., Xn - сечений процесса в моменты t1,...,tn. Многомерные ПВ играют существенную роль в теории СП. Поэтому более подробно обсудим их, начиная с простейших.
Одномерная ПВ p1(x1,t1) - ПВ случайной величины X(t1)=X1, является функцией двух переменных: значения функции x1 и момента ее отсчета t1ÎT, где T - область определения СП, например tÎ(0,T), tÎ(0,¥) и т.д. С помощью ПВ p 1(x1,t1) можно подсчитать математическое ожидание и дисперсию СП X(t) в произвольный момент t1ÎT, а также вероятность (Вер) того, что реализация x(t,w) процесса X(t) в момент t1 пройдет через "окно" a1<x<b1 (рис.3.2).
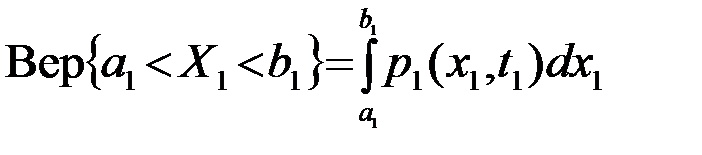 .(3.1.1)
.(3.1.1)

Рис 3.2
Если окно достаточно малое (a1, b1)=(x1, x1+D x), то
 .(3.1.2)
.(3.1.2)
Учитывая, что в одномерной ПВ p1(..) и в соотношениях, связанных с ней, используется один отсчетный момент t1ÎT и одно значение СП x1, индекс "1" часто опускают и вместо p1(x1,t1) пишут p1(x, t) или p(x,t).
Зная распределение мгновенных значений процесса X(t) в любой фиксированный момент времени t1, мы располагаем далеко неполной характеристикой процесса. Два процесса могут иметь одинаковые ПВ p1(x1, t1) и, следовательно, одинаковые характеристики, определяемые этой ПВ, но, тем не менее, существенно отличаются друг от друга. Например, один процесс может быстро флюктуировать, а другой - изменяться очень медленно. Это значит, что совместное распределение сечений X(t1)=X1 и X(t2)=X2, определяемое ПВ второго порядка p2(x1, t1; x2, t2), для этих процессов разное. ПВ второго порядка p2(x1, t1; x2, t2) определяется для всех возможных моментов отсчета t1, t2ÎT СП X(t) и поэтому в общем случае является функцией 4-х переменных: двух значений x1 и x2 реализации x(t,w) и двух моментов отсчета t1 и t2. Эта ПВ, в частности, определяет вероятность того, что реализация процессах x(t, w) в любые моменты t1, t2ÎT пройдет через "окна" x1Î(a1, b1), x2Î(a2, b2) (рис.3.2), а также смешанные моменты вида  . Здесь и в дальнейшем скобки вида
. Здесь и в дальнейшем скобки вида  означают статистическое усреднение (усреднение по ансамблю реализаций), т.е.
означают статистическое усреднение (усреднение по ансамблю реализаций), т.е.
 .(3.1.3)
.(3.1.3)
Из двумерной ПВ может быть получена одномерная ПВ
 .(3.1.4)
.(3.1.4)
Одномерная ПВ, как правило, не определяет двумерную ПВ. Двумерная ПВ, давая более полную характеристику СП x(t), чем одномерная ПВ, в свою очередь в общем случае не является исчерпывающей характеристикой СП. Она, в частности, не определяет смешанные моменты 3-сечений процесса X(t1)=X1, X(t2)=X2, X(t3)=X3, а именно  , а также вероятность прохождения траектории процесса через три "окна" в моменты времени t1, t2, t3. Ясно, что такое рассуждение можно продолжить. В результате придем к выводу: чем более высокого порядка n ПВ pn(x1, t1;...; xn, tn) находится в нашем распоряжении, тем более полными сведениями о СП X(t) мы располагаем. ПВ n-го порядка pn(x1, t1;...; xn, tn) определяет вероятность того, что реализация СП в моменты времени t1,..., tn пройдет через узкую полосу, образованную окнами (x1, x1+Dxn),..., (xn, xn+Dxn) (рис.3.3.). При достаточно большом n практически определяется вероятность любой траектории процесса.
, а также вероятность прохождения траектории процесса через три "окна" в моменты времени t1, t2, t3. Ясно, что такое рассуждение можно продолжить. В результате придем к выводу: чем более высокого порядка n ПВ pn(x1, t1;...; xn, tn) находится в нашем распоряжении, тем более полными сведениями о СП X(t) мы располагаем. ПВ n-го порядка pn(x1, t1;...; xn, tn) определяет вероятность того, что реализация СП в моменты времени t1,..., tn пройдет через узкую полосу, образованную окнами (x1, x1+Dxn),..., (xn, xn+Dxn) (рис.3.3.). При достаточно большом n практически определяется вероятность любой траектории процесса.
Получение аналитических выражений для ПВ pn(x1, t1;...; xn, tn) высокого порядка в общем случае представляет весьма сложную математическую задачу. Исключение составляют несколько классов СП, для которых полное задание СП не требует знания ПВ высокого порядка или для которых эта ПВ определяется сравнительно просто. Именно такие СП в основном используются в качестве математических моделей сигналов и помех в теории РТС. Приведем краткую характеристику этих СП.

Рис. 3.3
Квазидетерминированные процессы. Квазидетерминированный процесс x(t, l) представляет собой детерминированную функцию x(..) времени t и случайного параметра l, скалярного или векторного  . В качестве примера можно привести гармоническое колебание:
. В качестве примера можно привести гармоническое колебание:
 , (3.1.5)
, (3.1.5)
если некоторые из его параметров, допустим, амплитуда А и начальная фаза j являются случайными величинами. Множество Lвозможных значений двумерной случайной величины l =(A, j) (например, L:{AÎ(0,¥), j Î(0,2p)} и совместная плотность вероятностей p(A, j) определяют множество возможных реализаций СП (5) и ПВ каждой его реализации. Таким образом, вероятностное задание квазидетерминированного процесса сводится к заданию множества Lвозможных значений параметра l и его ПВ p(l). Нет необходимости определять многомерные ПВ процесса X(t), хотя в принципе это можно сделать по заданным функции X(t, l) и ПВ p(l).
Случайные процессы с независимыми значениями. Эти СП характерны тем, что мгновенные значения (отсчеты) процесса X(t1)=X1 и X(t2)=X2 в любые несовпадающие моменты времени являются статистически независимыми случайными величинами. При этом многомерная ПВ pn(x1, t1;...; xn, tn) любого порядка n определяется одномерной ПВ p(x,t), а именно, равна произведению одномерных ПВ
 . (3.1.6)
. (3.1.6)
Марковские процессы. Основной характеристикой марковского процесса является так называемая ПВ перехода p(xi, ti | xi-1, ti-1), i=2,3,...,n, (ti >ti-1), которая представляет собой условную ПВ того, что в момент времени t=ti сечение процесса X(ti) примет значение xi при условии, что в момент t=ti-1<ti имело место равенство X(ti-1)=xi-1. Здесь и в дальнейшем там, где это не может привести к недоразумениям, ПВ различных случайных величин, являющиеся различными функциями, обозначаются одним и тем же символом p. Аналогично одним символом P обозначаются вероятности различных событий. Условные ПВ и условные вероятности отмечены наличием вертикальной черты в аргументе, справа от которой проставляются обусловленные величины или события. Для марковских процессов характерно, что условная ПВ при известном произвольном числе предшествующих значений процесса равна условной ПВ при условии, что известно лишь ближайшее предшествующее значение
 . (3.1.7)
. (3.1.7)
ПВ перехода p(xi, ti | xi-1, ti-1) для любых ti-1, tiÎT, где T - область определения процесса X(t), совместно с ПВ первого порядка p1(x1,t1) определяет ПВ марковского процесса любого порядка. Действительно

При дальнейшем аналогичном понижении порядка ПВ pn-1(×), pn-2(×) и т.д., получим
 . (3.1.8)
. (3.1.8)
Таким образом, ПВ второго порядка p2(xi,ti;xi-1,ti-1) обеспечивает полное вероятностное определение марковского процесса, так как по ней определяются фигурирующие в (8) ПВ 1-го порядка и ПВ перехода
 (3.1.9)
(3.1.9)
 .(3.1.10)
.(3.1.10)
Аппарат теории марковских процессов хорошо разработан и широко используется в теории РТС, технической кибернетике и физике. Мы используем марковские процессы в качестве моделей сообщений l (t) при изучении фильтрации процессов (гл.7).
Нормальные (гауссовские) процессы. Нормальным или гауссовским процессом называется СП X(t), у которого многомерная ПВ любого порядка n является нормальной. В частности, сечение процесса X(t1)=X1 в любой момент времени t1 - нормальная случайная величина. Соответственно одномерная ПВ p1(x1,t1) представляет собой гауссовскую кривую. Также нормальной случайной величиной является любой линейный функционал нормального СП. В дальнейшем мы подробно остановимся на определении различных свойств и характеристик гауссовского процесса, так как в большинстве теоретических исследований используется гауссовская модель помех радиоприему. Здесь же ограничимся обсуждением только некоторых особенностей процесса.
Нормальный СП является еще одним примером СП, у которого ПВ второго порядка p2() определяет многомерную ПВ pn() любого порядка n, и, следовательно, дает полное вероятностное описание СП. Особая роль нормальных СП связана с асимптотической нормальностью распределения сумм независимых случайных величин и СП (центральная предельная теорема теории вероятностей). Центральная предельная теорема теории вероятностей утверждает, что функция распределения суммы независимых малых случайных величин с ростом числа слагаемых сходится к нормальной (гауссовской) функции распределения. Исключительная важность этой теоремы заключается в том, что она дает теоретическое объяснение наблюдению: если исход случайного эксперимента определяется большим числом независимых факторов, влияние каждого из которых мало, то статистические свойства исходов такого эксперимента хорошо аппроксимируются гауссовским распределением. Это свойство позволяет во многих случаях обосновать целесообразность выбора модели помех и некоторых сообщений в виде гауссовского СП. Наконец, учитывая благоприятные аналитические свойства гауссовских и марковских процессов, если даже процесс имеет иной характер, его стремятся, идеализируя аппроксимировать гауссовской или (и) марковской моделью (СП может быть одновременно гауссовским и марковским).



 (2.10.1)
(2.10.1) , в общем случае комплексная, и несущая частота f 0 в значительной степени определяют качественные показатели системы и подлежат обоснованному выбору.
, в общем случае комплексная, и несущая частота f 0 в значительной степени определяют качественные показатели системы и подлежат обоснованному выбору. (2.10.2)
(2.10.2)
 , (2.10.3)
, (2.10.3) начальной фазы сигнала при отражении. Поэтому принимаемый сигнал
начальной фазы сигнала при отражении. Поэтому принимаемый сигнал (2.10.4)
(2.10.4) . (2.10.5)
. (2.10.5) (2.10.6)
(2.10.6) , (2.10.7)
, (2.10.7)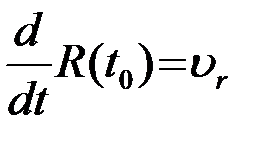 - радиальная скорость цели в момент t 0. Время запаздывания t (t) равно 2 R (t)/ c
- радиальная скорость цели в момент t 0. Время запаздывания t (t) равно 2 R (t)/ c ,
,
 ,
, .
. можно пренебречь. Условие, оправдывающее эту возможность и называемое условием узкополосности сигнала, сводится к следующему. Если на верхней частоте F с спектра огибающей
можно пренебречь. Условие, оправдывающее эту возможность и называемое условием узкополосности сигнала, сводится к следующему. Если на верхней частоте F с спектра огибающей  , (2.10.8)
, (2.10.8) (2.10.9)
(2.10.9) не несут полезной информации, называются несущественными и не подлежат измерению. В приведенном примере радиолокационного сигнала такими параметрами являются параметр интенсивности e и начальная фаза j.
не несут полезной информации, называются несущественными и не подлежат измерению. В приведенном примере радиолокационного сигнала такими параметрами являются параметр интенсивности e и начальная фаза j. (2.10.10)
(2.10.10) конечной длительности T с. Модели пачек отраженных импульсов будут подробнее рассмотрены в §5.5.
конечной длительности T с. Модели пачек отраженных импульсов будут подробнее рассмотрены в §5.5.
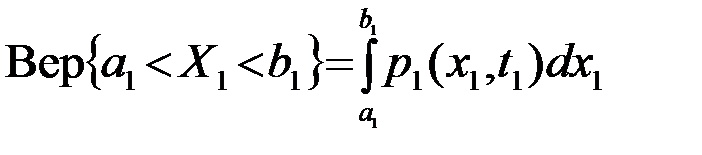 .(3.1.1)
.(3.1.1)
 .(3.1.2)
.(3.1.2) . Здесь и в дальнейшем скобки вида
. Здесь и в дальнейшем скобки вида  означают статистическое усреднение (усреднение по ансамблю реализаций), т.е.
означают статистическое усреднение (усреднение по ансамблю реализаций), т.е. .(3.1.3)
.(3.1.3) .(3.1.4)
.(3.1.4) , а также вероятность прохождения траектории процесса через три "окна" в моменты времени t1, t2, t3. Ясно, что такое рассуждение можно продолжить. В результате придем к выводу: чем более высокого порядка n ПВ pn(x1, t1;...; xn, tn) находится в нашем распоряжении, тем более полными сведениями о СП X(t) мы располагаем. ПВ n-го порядка pn(x1, t1;...; xn, tn) определяет вероятность того, что реализация СП в моменты времени t1,..., tn пройдет через узкую полосу, образованную окнами (x1, x1+Dxn),..., (xn, xn+Dxn) (рис.3.3.). При достаточно большом n практически определяется вероятность любой траектории процесса.
, а также вероятность прохождения траектории процесса через три "окна" в моменты времени t1, t2, t3. Ясно, что такое рассуждение можно продолжить. В результате придем к выводу: чем более высокого порядка n ПВ pn(x1, t1;...; xn, tn) находится в нашем распоряжении, тем более полными сведениями о СП X(t) мы располагаем. ПВ n-го порядка pn(x1, t1;...; xn, tn) определяет вероятность того, что реализация СП в моменты времени t1,..., tn пройдет через узкую полосу, образованную окнами (x1, x1+Dxn),..., (xn, xn+Dxn) (рис.3.3.). При достаточно большом n практически определяется вероятность любой траектории процесса.
 . В качестве примера можно привести гармоническое колебание:
. В качестве примера можно привести гармоническое колебание: , (3.1.5)
, (3.1.5) . (3.1.6)
. (3.1.6) . (3.1.7)
. (3.1.7)
 . (3.1.8)
. (3.1.8) (3.1.9)
(3.1.9) .(3.1.10)
.(3.1.10)


