Модуль 1. Общая теория статистики
Модульная единица 1.1. Предмет и метод статистики, статистика как общественная наука
Слово статистика произошло от латинского status – состояние. Введено в употребление немецким ученым Готфридом Ахенвалем.
В настоящее время термин “статистика” употребляется в трех значениях:
Статистикой называют отрасль практической деятельности, которая имеет целью сбор, обработку, анализ и публикацию массовых данных о различных явлений общественной жизни “статистический учет”
Статистикой называют цифровой материал, который характеризует общественные явления или территориальные распределения какого либо признака.
Статистикой называют отрасль знания, научную дисциплину, учебный предмет.
Предметом статистики является количественная сторона массовых общественных явлений, в неразрывной связи с их качественной стороной, ли их содержанием, а также количественное выражение закономерностей общественного развития в конкретных условия места и времени.
Предметом статистики является количественная сторона массовых значимых явлений и процессов, в неразрывной связи с их качественной стороной отражающей отвращающей присущее им своеобразие а также раскрывающая существующие закономерности развития в конкретных условиях места и времени.
Статистическая совокупность - это масса отдельных единиц, объединенных единой качественной стороной, но различающихся между собой по ряду признаков. Например: совокупностью будет КРС в, каком-либо хозяйстве, различающийся по полу, возрасту, и т.д.
Единица совокупности – это первичный элемент статистической совокупности, являющейся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счета.
Признак – это качественная особенн6ость единицы совокупности. По характеру отображения свойств изучаемой совокупности признаки делятся на две основные группы.
Количественные признаки – имеющие непосредственное количественное выражение (возраст, заработок и т.д.)
Атрибутивные (качественные) - признаки, не имеющие непосредственного количественного выражения, (например: профессии различаются характером труда: учитель, инженер и т. д.).
В случае, когда имеются противоположные по значению варианты признака, говорят об альтернативном признаке (да, нет). Например, продукция может быть годной или не годной.
Статистический показатель – это понятие (категория) отображающее количественные характеристики (размеры) статистической совокупности.
Статистические данные – это конкретные численные значения статистических показателей. Они всегда определенны не только количественно, но и качественно и зависят от условия места и времени.
Система статистических показателей - это совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями..
Метод статистики – это целая совокупность приемов, при помощи которых статистика исследует свой предмет. Она включает в себя три группы методов:
1. Метод массовых наблюдений
2. Метод группировок
3. Метод обобщающих показателей
По охвату единиц совокупности различают
1. сплошное наблюдение – регистрации подлежат все без исключения единицы совокупности.
2. не сплошное наблюдение, оно подразделяется на способы
· способ основного массива – обследованию подвергается основная часть совокупности, при этом сознательно игнорируется та часть совокупности, о которой заранее известно, что она не играет большой роли в характеристики совокупности (например, при исследовании урожайности зерновых по Красноярскому краю, можно заранее исключить Таймырский автономный округ)
· способ выборочного наблюдения – при данном способе обследованию подлежит не вся совокупность, а только отобранная в определенном порядке выборочная совокупность. Полученные в результате обследования выборочной совокупности результаты распространяют на всю совокупность.
· монографическое наблюдение – изучается небольшое число или отдельные единицы совокупности для более углубленного изучения вопросов.
Правила расчета средних
1. Совокупность, по которой рассчитывается средняя, должна быть достаточна, многочисленна (не менее трех единиц), чем больше совокупность, тем точнее расчет средней.
2. Единицы совокупности должны быть однородны как в качественном плане (при расчете среднего роста не должны попасть данные веса), так и в количественном (средний уровень жизни по стране является лишь описательной характеристикой, но не типической характеристикой, и в данном случае все население страны необходимо разбить на группы, которые отражают достаток, и рассчитывать групповые средние).
Общая формула степенной простой средней:
 . (5.1)
. (5.1)
Общая формула степенной взвешенной средней:
 , (5.2)
, (5.2)
где  - степенная средняя;
- степенная средняя;
 -индивидуальное значение для i -й единицы совокупности;
-индивидуальное значение для i -й единицы совокупности;
 - знак степени;
- знак степени;
 - знак суммирования;
- знак суммирования;
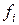 - частота, с которой в совокупности появляется i -о значение варианты.
- частота, с которой в совокупности появляется i -о значение варианты.
Средняя арифметическая простая:
 . (5.3)
. (5.3)
Средняя арифметическая взвешенная:
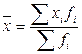 . (5.4)
. (5.4)
Основные свойства дисперсии
1. Если из каждого значения варианты отнять (прибавить) одно и то же постоянное число А, то средний квадрат отклонений от этого не изменится:
 , (5.34)
, (5.34)
Отсюда следует, что дисперсию можно рассчитать не только по заданным вариантам, но и по отклонениям этих вариант от какого-то постоянного числа:
 , (5.35)
, (5.35)
2. Если каждое значение вариант разделить или умножить на одно и то же постоянное число А, то дисперсия уменьшится (увеличится) от этого в А2 раз, а стандартное отклонение (среднее квадратическое отклонение) – в А раз:
 , (5.36)
, (5.36)
Отсюда следует, что все варианты можно разделить на какое-то одно и то же постоянное число (например, интервал ряда), рассчитать среднее квадратическое отклонение, а затем умножить его на это постоянное число: 
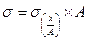 , (5.37)
, (5.37)
3. Средний квадрат отклонений, рассчитанный от средней величины, всегда будет меньше среднего квадрата отклонений, рассчитанного от любой другой величины А (свойство минимизации): 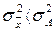 , причем больше на квадрат разности между средней
, причем больше на квадрат разности между средней  и этой величиной А, т.е. на
и этой величиной А, т.е. на  . Данное правило можно записать как:
. Данное правило можно записать как:
 или
или  (5.38)
(5.38)
Базисный абсолютный прирост
 (6.2)
(6.2)
1. если динамический ряд обозначить как:  то,
то,
· цепной абсолютный прирост рассчитывается как
· 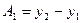



· Цепной абсолютный прирост называют скоростью роста.
· базисный абсолютный прирост рассчитывается как
· 



2. если динамический ряд обозначить как:  то,
то,
· цепной абсолютный прирост рассчитывается как
· 


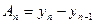
· базисный абсолютный прирост рассчитывается как
· 



Абсолютные приросты могут быть как положительные, так и отрицательные.
Коэффициент роста  – отношение текущего уровня ряда динамики к уровню принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %
– отношение текущего уровня ряда динамики к уровню принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %  . Коэффициент роста показывает во сколько раз уровень текущего периода выше или ниже уровня базисного периода, темп роста – сколько процентов он составил по отношению к базисному уровню.
. Коэффициент роста показывает во сколько раз уровень текущего периода выше или ниже уровня базисного периода, темп роста – сколько процентов он составил по отношению к базисному уровню.
1. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент роста рассчитывается как
· 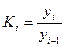 (6.3)
(6.3)
· 
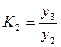
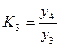

· базисный коэффициент роста рассчитывается как
·  (6.4)
(6.4)
· 
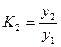


· последняя формула показывает коэффициент роста за весь период.
2. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент роста рассчитывается как
· 
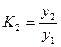


· базисный коэффициент роста рассчитывается как
· 



последняя формула показывает коэффициент роста за весь период.
Коэффициент (темп) роста всегда число положительное.
Коэффициент (темп) прироста  показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%), то есть, сколько частей (процентов) составляет относительный прирост данного уровня по отношению к базисному уровню. Рассчитывается двумя способами:
показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%), то есть, сколько частей (процентов) составляет относительный прирост данного уровня по отношению к базисному уровню. Рассчитывается двумя способами:
Первый способ - как отношение абсолютного прироста к базисному уровню.
1. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент прироста рассчитывается как
·  (6.5)
(6.5)
· 
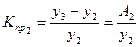


· базисный коэффициент прироста рассчитывается как
·  (6.6)
(6.6)
· 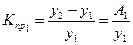


 последняя формула показывает коэффициент прироста за весь период
последняя формула показывает коэффициент прироста за весь период
2. если динамический ряд обозначить как:  то,
то,
· цепной коэффициент прироста рассчитывается как
· 



· базисный коэффициент прироста рассчитывается как
· 



последняя формула показывает коэффициент прироста за весь период
Второй способ – коэффициент (темп) роста минус 1 (100).
 или
или 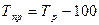 (6.8)
(6.8)
Коэффициент (темп) прироста может быть как положительным, так и отрицательным.
Абсолютное значение одного процента прироста показывает часть абсолютного прироста, которая обеспечила 1% относительного прироста. Рассчитывается двумя способами.
Первый способ – как отношение абсолютного прироста к темпу прироста за тот же период
 (6.9)
(6.9)
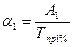
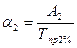

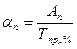
Второй способ – как 0,01 часть от предыдущего (базисного) уровня.
 (6.10)
(6.10)
Для обобщения характеристики динамики, рассчитанной по уровням динамического ряда, определяют средние показатели динамического ряда. Средние показатели динамического ряда подразделяются на:
Средние уровни ряда.
В зависимости от вида временного ряда выбирают следующие методы расчета среднего уровня ряда:
Для интервального ряда динамики с равными интервалами средний уровень ряда  рассчитывается как средняя арифметическая простая исходных уровней
рассчитывается как средняя арифметическая простая исходных уровней
 (6.11)
(6.11)
где n – число уровней динамического ряда.
Для расчета среднего уровня моментного ряда динамики с равными отрезками между датами средний уровень определяют как среднюю хронологическую.

 (6.12)
(6.12)
где  – порядковый номер последнего уровня, если первый уровень динамического ряда обозначается как
– порядковый номер последнего уровня, если первый уровень динамического ряда обозначается как 
 (6.13)
(6.13)
Для интервального ряда динамики с неравными интервалами средний уровень ряда  рассчитывается как средняя арифметическая взвешенная
рассчитывается как средняя арифметическая взвешенная
 (6.14)
(6.14)
где  - продолжительность периода между датами.
- продолжительность периода между датами.
С редние показатели изменения уровней ряда (средний абсолютный прирост, средние коэффициенты (темпы) роста и прироста)
Средний абсолютный прирост (средняя скорость роста)  определяется как средняя арифметическая из показателей абсолютного прироста.
определяется как средняя арифметическая из показателей абсолютного прироста.
 (6.15)
(6.15)
где  - количество абсолютных приростов.
- количество абсолютных приростов.
Средний коэффициент (темп) роста рассчитывается по формуле средней геометрической из индивидуальных коэффициентов (темпов) роста, так как необходимо учитывать, то обстоятельство, что скорость развития явления идет по правилам сложных процентов, где накапливается процент на процент.
если динамический ряд обозначить как: 
 (6.16)
(6.16)
где
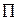 - знак произведения
- знак произведения
 – число коэффициентов роста.
– число коэффициентов роста.
Корни высоких степеней находятся логарифмированием, для чего прологарифмируем левую и правую части уравнения:
 (6.17)
(6.17)
Если использовать взаимосвязи, существующие между коэффициентами роста, вычисленными с переменной базой (цепные показатели), и коэффициентами роста, вычисленными с постоянной базой (базисные показатели), т.е. учитывая, что  , и динамический ряд обозначен:
, и динамический ряд обозначен:  - средний коэффициент роста можно определить по формуле:
- средний коэффициент роста можно определить по формуле:
 (6.18)
(6.18)
где  – число уровней динамического ряда.
– число уровней динамического ряда.
Средний коэффициент (темп) прироста рассчитать по индивидуальным коэффициентам (темпам) прироста, с помощью средней геометрической, нельзя, так как темпы прироста могут иметь отрицательные значения, а отрицательные числа логарифмов не имеют. Поэтому средний коэффициент (темп) прироста рассчитывают как:
 или
или  (6.19)
(6.19)
1.6.2 Выявление и характеристика основной тенденции развития
Расчет показателей динамики, как правило, является только первым этапом статистического исследования рядов динамики. Дальнейший анализ заключается в более сложных обобщениях, с определением основной тенденции развития, колеблемости уровней и связи рядов, прогнозированием развития явления на будущие периоды.
Если тренд отсутствует, то
· для каждого конкретного месяца (квартала, недели и т.д.):
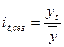 (6.48)
(6.48)
где  - уровень динамического ряда за месяц (квартал, неделю и т.д.)
- уровень динамического ряда за месяц (квартал, неделю и т.д.)
 - средний уровень за весь период (год, квартал и т.д.)
- средний уровень за весь период (год, квартал и т.д.)
· для больших (средних) промежутков времени (за несколько месяцев, кварталов и т.д.)
 или
или 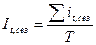 (6.49)
(6.49)
где 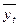 - средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.)
- средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.)
 - число лет.
- число лет.
2. Если в динамическом ряду существует ярко выраженный тренд, расчет проводится следующим образом
а) для каждого уровня определяют значения выровненного уровня
b) рассчитывают, как отношение фактического уровня динамического ряда к выровненному уровню по тренду либо как отношение средней из фактических уровней одноименных месяцев (кварталов, недель и т.д.) к средней из выровненных данных по тем же месяцам (кварталам, неделям и т.д.).
 либо
либо  (6.50)
(6.50)
c) также находят среднее из отношений фактических уровней к выровненному уровню для одноименных месяцев (кварталов, недель и т.д.)
 (6.51)
(6.51)
где  - число лет
- число лет
1.6.2.5 Экстраполяция и интерполяция
Исследование динамических рядов социально-экономических явлений, определения закономерности их развития во времени создают основу для статистического прогнозирования (экстраполяции) и интерполяции изучаемого явления.
Экстраполяция в динамике предполагает распространение полученных выводов, полученных в прошлом на будущее время. При этом предполагается, что закономерность развития, динамического ряда сохраняется в будущем.
Самый простой метод экстраполяции это применение средних характеристик ряда динамики: среднего абсолютного прироста и среднего темпа роста.
Более часто применяют экстраполяцию динамического ряда по аналитически выровненным рядам.
После того как по фактическому динамическому ряду выявлен тренд (выровненный ряд, отражающий тенденцию развития) экстраполяцию можно провести двумя методами:
1. графический метод. Заключается в построении точного графика выровненного динамического ряда, на котором линию полученного тренда продлевают до интересующей нас даты.
2. аналитический метод. При данном методе в рассчитанное аналитическое уравнение подставляют номер интересующего нас периода.
Выявление основной тенденции развития дает возможность определять также значение недостающего члена ряда – интерполяция. Также проводится графическим и аналитическим методом.
Частные уравнения регрессии
Частные уравнения регрессии, рассчитываются на основе множественного уравнения регрессии:
 (9.139)
(9.139)
Они показывают изолированное влияние одного конкретного  фактора на результативный признак
фактора на результативный признак  , при зафиксированном, на среднем уровне, положении остальных, включенных в модель факторов. Влияния зафиксированных факторов в уравнениях частной регрессии присоединены к свободному члену уравнения регрессии
, при зафиксированном, на среднем уровне, положении остальных, включенных в модель факторов. Влияния зафиксированных факторов в уравнениях частной регрессии присоединены к свободному члену уравнения регрессии  .
.
Частные множественные регрессии записываются, как:
 (9.140)
(9.140)
Обозначение  показывает, что изучается влияние на результат
показывает, что изучается влияние на результат  , фактора
, фактора  , при зафиксированном на среднем уровне положении факторов
, при зафиксированном на среднем уровне положении факторов  . Обозначение
. Обозначение  показывает, что изучается влияние на результат
показывает, что изучается влияние на результат  , фактора
, фактора  , при зафиксированном на среднем уровне положении факторов
, при зафиксированном на среднем уровне положении факторов  , и т, д. Знак
, и т, д. Знак  в нижнем индексе обозначения отделяет фактор влияния, которого исследуется, от факторов, влияние которых изолируется.
в нижнем индексе обозначения отделяет фактор влияния, которого исследуется, от факторов, влияние которых изолируется.
Частные уравнения множественной регрессии для линейной модели имеют вид:
 (9.141)
(9.141)
На основе частных уравнений регрессии рассчитывают частные коэффициенты эластичности:
 (9.142)
(9.142)
Частные коэффициенты эластичности отличаются от средних коэффициентов.
Частный коэффициент эластичности показывает, на сколько, в среднем, процентов изменится результат при подстановке в уравнение регрессии конкретного значения 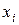 .
.
Средний коэффициент эластичности  показывает, на сколько в среднем процентов изменится результат, если соответствующий данному коэффициенту фактор увеличится на 1%, при зафиксированных, на средних уровнях величин остальных, включенных в модель, факторов.
показывает, на сколько в среднем процентов изменится результат, если соответствующий данному коэффициенту фактор увеличится на 1%, при зафиксированных, на средних уровнях величин остальных, включенных в модель, факторов.
 (9.143)
(9.143)
1.9.4.6.3 Множественная корреляция
Силу связи во множественных моделях изучают с помощью показателя множественной корреляции и его квадрата – показателя множественной детерминации.
Показатель множественной корреляции  – показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Может принимать значения от 0 до 1, то есть в отличие от парной модели не показывает направление связи.
– показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Может принимать значения от 0 до 1, то есть в отличие от парной модели не показывает направление связи.
Показатель множественной детерминации  - показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов.
- показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов.
В статистике и эконометрике показатель множественной корреляции (детерминации) принято называть индексом или коэффициентом множественной (совокупной) корреляции.
Для линейной множественной функции и для функций нелинейных по переменным (полиномы разных степеней, равносторонняя гипербола и т.п. функции) индекс множественной корреляции совпадает скоэффициентом множественной корреляции.
Коэффициент (индекс) множественной корреляции рассчитывают, используя следующие формулы:
 (9.144)
(9.144)
где:
 - остаточная дисперсия (9.145)
- остаточная дисперсия (9.145)
 - общая дисперсия для признака
- общая дисперсия для признака  (9.146)
(9.146)
 (9.147)
(9.147)
Коэффициент множественной корреляции можно рассчитать и, как:
 (9.148)
(9.148)
где:
 - парные коэффициенты корреляции между результативным признаком
- парные коэффициенты корреляции между результативным признаком  и одним из факторов
и одним из факторов 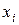 .
.
Для функций нелинейных по оцениваемым параметрам (степенная, показательная, экспоненциальная и т. п. функции) индекс множественной корреляции не совпадает скоэффициентом множественной корреляции. Его называют « » и определяют как
» и определяют как
 (9.149)
(9.149)
Коэффициенты (индексы) множественной детерминации получают, возводя коэффициенты (индексы) корреляции в квадрат, или по формулам.
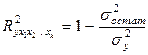 (9.150)
(9.150)
 (9.151)
(9.151)
 (9.152)
(9.152)
Частная корреляция
Множественный коэффициент (индекс) корреляции показывает тесноту связи между результатом и всеми включенными в модель факторами, для того, чтобы изучить силу связи между результатом и только одним из включенных в модель факторов, рассчитывают частные коэффициенты корреляции, для каждого из факторов включенных в модель.
Частный коэффициент корреляции показывает тесноту связи между результативным признаком  и только одним фактором
и только одним фактором  при элиминировании (устранении) влияния всех остальных включенных в модель факторов.
при элиминировании (устранении) влияния всех остальных включенных в модель факторов.
В зависимости от того, влияние скольких факторов необходимо исключать различают частные коэффициенты разных порядков: нулевого, первого, второго, третьего и т.д. Так, например:
· Коэффициенты частной корреляции нулевого порядка – коэффициенты парной корреляции, так как нет необходимости устранять влияние даже одного фактора.
· Коэффициенты частной корреляции первого порядка – коэффициенты частной корреляции, в которых элиминируется влияние одного фактора ( ,
,  ,
,  и т.д.).
и т.д.).
· Коэффициенты корреляции второго порядка – коэффициенты частной корреляции, в которых элиминируется влияние двух факторов ( ,
,  ,
,  и т.д.) и так далее.
и т.д.) и так далее.
Коэффициенты частной корреляции более высоких порядков рассчитываются через коэффициенты корреляции более низких порядков. Коэффициенты первого порядка через коэффициенты нулевого порядка, второго порядка через коэффициенты первого порядка и т.д. Рекуррентная формула для расчета коэффициентов частной корреляции  порядка имеет вид:
порядка имеет вид:
 (9.157)
(9.157)
Коэффициенты частной корреляции могут принимать значения в пределах от -1 до 1.
Также частные коэффициенты корреляции можно рассчитать через множественные коэффициенты детерминации. Так коэффициент частной корреляции второго порядка рассчитывается как:
 или
или  и т.д. (9.158)
и т.д. (9.158)
В общем виде уравнение для расчета коэффициентов частной корреляции  порядка имеет вид:
порядка имеет вид:
 (9.159)
(9.159)
где
 - коэффициент множественной детерминации
- коэффициент множественной детерминации  для всех факторов.
для всех факторов.
 - коэффициент множественной детерминации без включения в модель фактора
- коэффициент множественной детерминации без включения в модель фактора  .
.
Рассчитанные через множественные коэффициенты детерминации частные коэффициенты корреляции могут принимать значения в интервале от 0 до 1.
Кроме того, частные коэффициенты корреляции можно рассчитать через  . Так, например, частные коэффициенты корреляции первого порядка для двухфакторной линейной модели, выраженной в стандартизованном масштабе
. Так, например, частные коэффициенты корреляции первого порядка для двухфакторной линейной модели, выраженной в стандартизованном масштабе  :
:
 (9.160)
(9.160)
Отсюда:
 и
и  (9.161)
(9.161)
Возводя в квадрат коэффициенты частной корреляции, получают коэффициенты частной детерминации.
Частные коэффициенты корреляции используют при формировании корреляционно-регрессионной модели, для отбора факторов. При этом из модели исключают факторы несущественные по критерию Стьюдента.
Коэффициент частной детерминации показывает долю вариации результативного признака дополнительно сложившуюся при включении в модель фактора 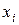 , в вариации признака, не объясненную включенными до этого в модель факторами. Можно рассчитать по формуле на основе коэффициентов множественной детерминации.
, в вариации признака, не объясненную включенными до этого в модель факторами. Можно рассчитать по формуле на основе коэффициентов множественной детерминации.
 (9.162)
(9.162)
где
 - коэффициент множественной детерминации
- коэффициент множественной детерминации  для всех факторов.
для всех факторов.
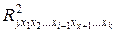 - коэффициент множественной детерминации без включения в модель фактора
- коэффициент множественной детерминации без включения в модель фактора  .
.
Зная коэффициенты частной детерминации, последовательно нулевого, первого, второго и более высоких порядков, определяют коэффициент множественной корреляции.
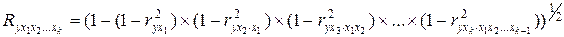 (156)
(156)
1.9.4.7 Оценка надежности параметров множественной регрессии и корреляции
Оценка значимости множественного уравнения регрессии в целом проводится с помощью  , (критерия Фишера).
, (критерия Фишера).
 (9.163)
(9.163)
где:
 – факторная дисперсия (9.164)
– факторная дисперсия (9.164)
 – остаточная дисперсия (9.165)
– остаточная дисперсия (9.165)
F-критерий можно рассчитать и по формуле:
 (9.166)
(9.166)
где:
 - для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели
- для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели  - число параметров при
- число параметров при  и их линеаризации (
и их линеаризации ( и так далее), которое может быть больше числа факторов
и так далее), которое может быть больше числа факторов
 - число наблюдений
- число наблюдений
Если расчетный  превышает табличный при определенном уровне значимости
превышает табличный при определенном уровне значимости  или
или  , и числе свободы -
, и числе свободы -  ,
,  (таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо.
(таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо.
Величина  позволяет также оценить статистическую значимость и коэффициента (индекса) множественной корреляции
позволяет также оценить статистическую значимость и коэффициента (индекса) множественной корреляции  .
.
Кроме оценки уравнения в целом, большое практическое значение имеет статистическая оценка значимости каждого отдельно включенного в модель фактора, через частные критерии Фишера  , (
, ( ). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.
). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.
Расчет частного  , для фактора
, для фактора 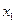 проводится по формуле:
проводится по формуле:
 (9.167)
(9.167)
 - коэффициент множественной детерминации для модели, включающей все факторы
- коэффициент множественной детерминации для модели, включающей все факторы
 - коэффициент множественной детерминации для модели, без включения фактора
- коэффициент множественной детерминации для модели, без включения фактора 
Расчета частного  в общем виде, для фактора
в общем виде, для фактора  проводится по формуле:
проводится по формуле:
 (9.168)
(9.168)
Расчета частного  , для оценки значимости влияния фактора
, для оценки значимости влияния фактора  после включения в модель других факторов проводится по формуле:
после включения в модель других факторов проводится по формуле:
 (9.169)
(9.169)
Если величина расчетного частного  превышает величину табличного при определенном уровне значимости
превышает величину табличного при определенном уровне значимости  или
или  , и числе свободы -
, и числе свободы -  ,
,  (таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора
(таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора  , после введения в модель остальных факторов, целесообразно. Если величина расчетного частного
, после введения в модель остальных факторов, целесообразно. Если величина расчетного частного  меньше табличного значения, можно сказать, что включение в модель фактора
меньше табличного значения, можно сказать, что включение в модель фактора  , после введения в модель остальных факторов, статистически неоправданно, и его необходимо исключить из рассматриваемой модели.
, после введения в модель остальных факторов, статистически неоправданно, и его необходимо исключить из рассматриваемой модели.
Зная величину частного критерия Фишера 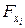 , рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии
, рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии 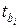 .
.
 (9.170)
(9.170)
Критерий Стьюдента  так
так



 . (5.1)
. (5.1) , (5.2)
, (5.2) - степенная средняя;
- степенная средняя; -индивидуальное значение для i -й единицы совокупности;
-индивидуальное значение для i -й единицы совокупности; - знак степени;
- знак степени; - знак суммирования;
- знак суммирования;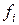 - частота, с которой в совокупности появляется i -о значение варианты.
- частота, с которой в совокупности появляется i -о значение варианты. . (5.3)
. (5.3)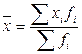 . (5.4)
. (5.4) , (5.34)
, (5.34) , (5.35)
, (5.35) , (5.36)
, (5.36)
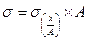 , (5.37)
, (5.37)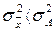 , причем больше на квадрат разности между средней
, причем больше на квадрат разности между средней  и этой величиной А, т.е. на
и этой величиной А, т.е. на  . Данное правило можно записать как:
. Данное правило можно записать как: или
или  (5.38)
(5.38) (6.2)
(6.2) то,
то,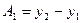







 то,
то,


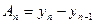



 – отношение текущего уровня ряда динамики к уровню принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %
– отношение текущего уровня ряда динамики к уровню принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %  . Коэффициент роста показывает во сколько раз уровень текущего периода выше или ниже уровня базисного периода, темп роста – сколько процентов он составил по отношению к базисному уровню.
. Коэффициент роста показывает во сколько раз уровень текущего периода выше или ниже уровня базисного периода, темп роста – сколько процентов он составил по отношению к базисному уровню.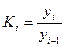 (6.3)
(6.3)
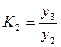
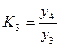

 (6.4)
(6.4)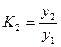








 показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%), то есть, сколько частей (процентов) составляет относительный прирост данного уровня по отношению к базисному уровню. Рассчитывается двумя способами:
показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%), то есть, сколько частей (процентов) составляет относительный прирост данного уровня по отношению к базисному уровню. Рассчитывается двумя способами: (6.5)
(6.5)
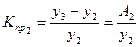


 (6.6)
(6.6)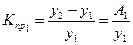


 последняя формула показывает коэффициент прироста за весь период
последняя формула показывает коэффициент прироста за весь период





 или
или 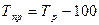 (6.8)
(6.8) (6.9)
(6.9)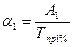
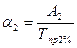

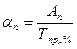
 (6.10)
(6.10) рассчитывается как средняя арифметическая простая исходных уровней
рассчитывается как средняя арифметическая простая исходных уровней (6.11)
(6.11) (6.12)
(6.12) – порядковый номер последнего уровня, если первый уровень динамического ряда обозначается как
– порядковый номер последнего уровня, если первый уровень динамического ряда обозначается как 
 (6.13)
(6.13) (6.14)
(6.14) - продолжительность периода между датами.
- продолжительность периода между датами. определяется как средняя арифметическая из показателей абсолютного прироста.
определяется как средняя арифметическая из показателей абсолютного прироста. (6.15)
(6.15) (6.16)
(6.16)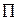 - знак произведения
- знак произведения (6.17)
(6.17) , и динамический ряд обозначен:
, и динамический ряд обозначен:  - средний коэффициент роста можно определить по формуле:
- средний коэффициент роста можно определить по формуле: (6.18)
(6.18) или
или  (6.19)
(6.19)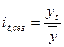 (6.48)
(6.48) - уровень динамического ряда за месяц (квартал, неделю и т.д.)
- уровень динамического ряда за месяц (квартал, неделю и т.д.) или
или 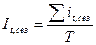 (6.49)
(6.49)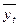 - средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.)
- средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.) - число лет.
- число лет. либо
либо  (6.50)
(6.50) (6.51)
(6.51) (9.139)
(9.139) фактора на результативный признак
фактора на результативный признак  , при зафиксированном, на среднем уровне, положении остальных, включенных в модель факторов. Влияния зафиксированных факторов в уравнениях частной регрессии присоединены к свободному члену уравнения регрессии
, при зафиксированном, на среднем уровне, положении остальных, включенных в модель факторов. Влияния зафиксированных факторов в уравнениях частной регрессии присоединены к свободному члену уравнения регрессии  .
. (9.140)
(9.140) показывает, что изучается влияние на результат
показывает, что изучается влияние на результат  , фактора
, фактора  , при зафиксированном на среднем уровне положении факторов
, при зафиксированном на среднем уровне положении факторов  . Обозначение
. Обозначение  показывает, что изучается влияние на результат
показывает, что изучается влияние на результат  , при зафиксированном на среднем уровне положении факторов
, при зафиксированном на среднем уровне положении факторов  , и т, д. Знак
, и т, д. Знак  в нижнем индексе обозначения отделяет фактор влияния, которого исследуется, от факторов, влияние которых изолируется.
в нижнем индексе обозначения отделяет фактор влияния, которого исследуется, от факторов, влияние которых изолируется. (9.141)
(9.141) (9.142)
(9.142)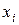 .
. показывает, на сколько в среднем процентов изменится результат, если соответствующий данному коэффициенту фактор увеличится на 1%, при зафиксированных, на средних уровнях величин остальных, включенных в модель, факторов.
показывает, на сколько в среднем процентов изменится результат, если соответствующий данному коэффициенту фактор увеличится на 1%, при зафиксированных, на средних уровнях величин остальных, включенных в модель, факторов. (9.143)
(9.143) – показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Может принимать значения от 0 до 1, то есть в отличие от парной модели не показывает направление связи.
– показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Может принимать значения от 0 до 1, то есть в отличие от парной модели не показывает направление связи. - показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов.
- показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов. (9.144)
(9.144) - остаточная дисперсия (9.145)
- остаточная дисперсия (9.145) - общая дисперсия для признака
- общая дисперсия для признака  (9.147)
(9.147) (9.148)
(9.148) - парные коэффициенты корреляции между результативным признаком
- парные коэффициенты корреляции между результативным признаком  » и определяют как
» и определяют как (9.149)
(9.149)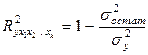 (9.150)
(9.150) (9.151)
(9.151) (9.152)
(9.152) ,
,  ,
,  и т.д.).
и т.д.). ,
,  ,
,  и т.д.) и так далее.
и т.д.) и так далее. порядка имеет вид:
порядка имеет вид: (9.157)
(9.157) или
или  и т.д. (9.158)
и т.д. (9.158) (9.159)
(9.159) - коэффициент множественной детерминации
- коэффициент множественной детерминации  - коэффициент множественной детерминации без включения в модель фактора
- коэффициент множественной детерминации без включения в модель фактора  . Так, например, частные коэффициенты корреляции первого порядка для двухфакторной линейной модели, выраженной в стандартизованном масштабе
. Так, например, частные коэффициенты корреляции первого порядка для двухфакторной линейной модели, выраженной в стандартизованном масштабе  :
: (9.160)
(9.160) и
и  (9.161)
(9.161) (9.162)
(9.162)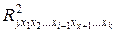 - коэффициент множественной детерминации без включения в модель фактора
- коэффициент множественной детерминации без включения в модель фактора  .
.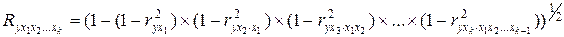 (156)
(156) , (критерия Фишера).
, (критерия Фишера). (9.163)
(9.163) – факторная дисперсия (9.164)
– факторная дисперсия (9.164) – остаточная дисперсия (9.165)
– остаточная дисперсия (9.165) (9.166)
(9.166) и их линеаризации (
и их линеаризации ( и так далее), которое может быть больше числа факторов
и так далее), которое может быть больше числа факторов - число наблюдений
- число наблюдений превышает табличный при определенном уровне значимости
превышает табличный при определенном уровне значимости  или
или  , и числе свободы -
, и числе свободы -  ,
,  (таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо.
(таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо. .
. , (
, ( ). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.
). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.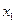 проводится по формуле:
проводится по формуле: (9.167)
(9.167) - коэффициент множественной детерминации для модели, включающей все факторы
- коэффициент множественной детерминации для модели, включающей все факторы - коэффициент множественной детерминации для модели, без включения фактора
- коэффициент множественной детерминации для модели, без включения фактора  (9.168)
(9.168) после включения в модель других факторов проводится по формуле:
после включения в модель других факторов проводится по формуле: (9.169)
(9.169) превышает величину табличного при определенном уровне значимости
превышает величину табличного при определенном уровне значимости  , и числе свободы -
, и числе свободы -  ,
,  (таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора
(таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора 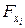 , рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии
, рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии 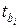 .
. (9.170)
(9.170) так
так


