

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Декартова система координат является наиболее распространенной для описания движения жидкости в трехмерном пространстве.
Рассмотрим представление всех рассмотренных понятий и операций в декартовой системе координат, обращая главное внимание лишь на физическое содержание векторных операций и правила их использования и не ставя перед собой задачу строгого доказательства тех или иных положений.
С учетом этого сразу можем написать
1.  (3.31)
(3.31)
Таким образом, проекции вектора набла на оси прямоугольной декартовой системы координат есть операторы (производные)  . Поэтому умножить проекцию вектора набла
. Поэтому умножить проекцию вектора набла
Примечание:
5. скалярные операторы 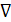 2…
2…
6. (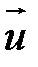
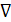 )…
)…
будучи примененными к скалярной функции  , дадут зависимости:
, дадут зависимости:


Если  есть вектор, то, представляя его тремя скалярными функциями
есть вектор, то, представляя его тремя скалярными функциями  x;
x;  y;
y;  z (проекции на оси координат) для
z (проекции на оси координат) для 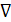 2
2  и (
и (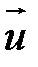
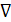 )
)  получим по три формулы, аналогичные приведенным (выше).
получим по три формулы, аналогичные приведенным (выше).
Например:

на проекцию какого-либо другого вектора – это значит продифференцировать ее по соответствующей координате.
Учитывая это и применяя правило действия над векторами, получаем:
2.  (3.32)
(3.32)
3.  (3.33)
(3.33)
4. 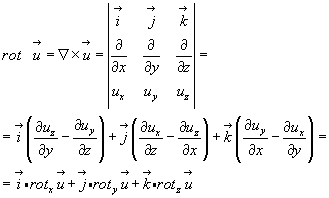 (3.34)
(3.34)
5.  (3.35)
(3.35)
6. 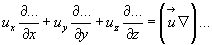 (3.36)
(3.36)
3.4.1. Примеры, имеющие самостоятельное значение
1. Положение точки или частицы жидкости в декартовой системе координат характеризуется радиус-вектором 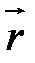

С помощью этого вектора распределене скоростей в пространстве дается соотношением 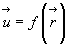 , что эквивалентно трем скалярным уравнениям:
, что эквивалентно трем скалярным уравнениям:

Приращение вектора 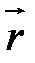 - величина d
- величина d 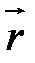 (расстояние между двумя близкими точками) определяется равенством:
(расстояние между двумя близкими точками) определяется равенством:

а скорость движения некоторой частицы представляется очевидным соотношением

где D – символ субстационарной производной.
Умножим элементарный вектор d 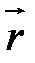 на градиент некоторой скалярной функции φ:
на градиент некоторой скалярной функции φ:
|
|

Замечаем, что правая часть этого равенства представляет собой полный дифференциал скалярной функции φ.
Т.о. имеем важную формулу:
 (3.37)
(3.37)
2. Составим скалярное произведение единичного вектора  и grad φ:
и grad φ:

(здесь единичный вектор  в проекциях на оси координат представляется равенством:
в проекциях на оси координат представляется равенством:
 )
)
Найдем производную от φ по направлению 

т.к.

то

Замечание:
Из формулы (3.38) видно, что производная 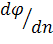 достигает своего наибольшего значения для направления
достигает своего наибольшего значения для направления  , совпадающего с направлением grad φ, при этом ее наибольшее значение равно величине grad φ. Поэтому градиент скалярной функции можем определять как вектор, имеющий направление быстрейшего роста скалярной величины φ и равный производной от нее по этому направлению.
, совпадающего с направлением grad φ, при этом ее наибольшее значение равно величине grad φ. Поэтому градиент скалярной функции можем определять как вектор, имеющий направление быстрейшего роста скалярной величины φ и равный производной от нее по этому направлению.
Именно поэтому, например, результирующая сила давления равна – grad P, т.к. она должна быть направлена в сторону быстрейшего падения давления, а результирующий тепловой поток – в сторону наибольшего уменьшения температуры, т.е. в сторону – grad T, как это следует из закона Фурье.
Замечание к разделу:
Координатное представление вектора набла позволяет во многих случаях упрощать формулы, записанные в символическом виде, и, таким образом, является существенным дополнением к нему.
Пример:
Найдем выражение для  , где
, где  - постоянный вектор:
- постоянный вектор:

Далее, из соотношений сделанных при выводе формулы (3.28), получаем

В этом выражении последующие преобразования невозможны.
Но, если обратиться к координатному представлению рассмотренных нами операций, сразу замечаем, что величина  оказывается равной
оказывается равной

т.о. 
rot 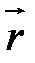 = 0, т.к. производные от одних независимых переменных по другим тождественно равны нулю (см. 3.34).
= 0, т.к. производные от одних независимых переменных по другим тождественно равны нулю (см. 3.34).
Кроме того:

т.о. получим простое соотношение:
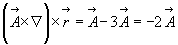
Казалось бы, что этот пример наталкивает на мысль, что символический метод совершенно не нужен, т.к. непосредственным вычислением в координатном представлении можно получить все необходимые преобразования.
|
|
Это действительно так, однако если попытаться вывести такие простые зависимости, как:



опираясь лишь на координатное выражение оператора Гамильтона, можно сразу оценить существенную экономию труда и бумаги, а также элегантность операций, которые сопутствуют символическому методу исчисления.
3.5. Преобразование объемных интегралов в поверхностные
Приведем без доказательства формулы Гаусса и Остроградского, известные из курса математического анализа, в символах векторного анализа.
Формула Гаусса:
 (3.39)
(3.39)
Формула Остроградского:
 (3.40)
(3.40)
Дифференциальные тензоры
Составим диадное произведение вектора набла 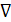 и какого-нибудь переменного вектора, например
и какого-нибудь переменного вектора, например 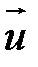 .
.
Помня, что умножить на составляющую символического вектора 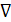 - это значит продифференцировать по соответствующей координате, находим:
- это значит продифференцировать по соответствующей координате, находим:
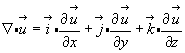 (3.44)
(3.44)
Этот тензор по аналогии с градиентом скалярной величины (см. формулу 3.33) назовем градиентом вектора:
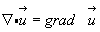 (3.42)
(3.42)
Его составляющие легко выявляются, если рассмотреть диадные произведения ортов на скалярные производные от вектора 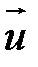 в равенстве (3.41), и записываются в виде матрицы:
в равенстве (3.41), и записываются в виде матрицы:
Примечание:
Свойство сопряженного тензора:
Величина произведения вектора на тензор, не изменится, если при перестановке сомножителей тензор заменить на сопряженный.
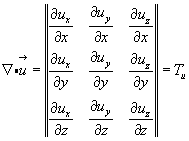 (3.43)
(3.43)
Умножим тензор grad 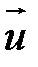 на дифференциал радиус вектора слева:
на дифференциал радиус вектора слева:
 (3.44)
(3.44)
Полученное соотношение совершенно аналогично (3.37) полному дифференциалу скалярной функции. Т.е. имеем:
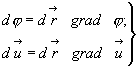 (3.44а)
(3.44а)
Если в тензоре (3.43) заменить элементы строк на элементы столбцов, то получим сопряженный тензор:
 (3.45)
(3.45)
Если в другой записи (с учетом (3.6) и (3.7)):
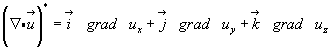 (3.46)
(3.46)
но по свойству сопряженного тензора равенство (3.44а) можно переписать в следующем виде:
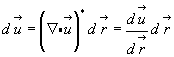 (3.47)
(3.47)
Следовательно, тензор (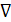 ∙
∙ 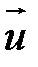 )* можно рассматривать как производную от векторной функции
)* можно рассматривать как производную от векторной функции 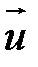 по векторному аргументу
по векторному аргументу 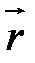 .
.
|
|
|

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!