

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Операции и теоремы Булевой алгебры
Основными операциями булевой алгебры являются операции логического сложения, умножения и отрицания.
Логическое сложение. Операция ИЛИ или дизъюнкцией. Она
соответствует математической операции объединения множеств.
Логическое умножение. Операция И или конъюнкцией. Она
соответствует математической операции пересечения множеств.
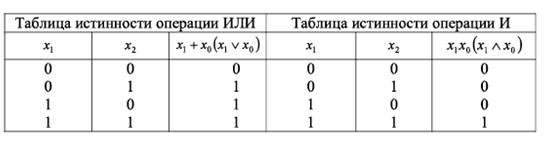
Отрицание. Инверсия или дополнение. Для ее обозначения используют черту над соответствующим выражением. Операция определяется постулатами:
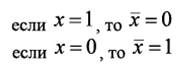
Теоремы булевой алгебры отражают связи, существующие между операциями, выполняемыми над логическими переменными.
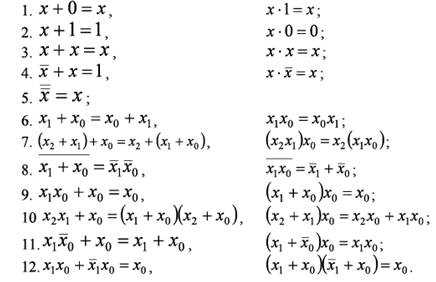
Логические элементы. Обозначение. Логические операции. Таблица истинности.
В соответствии с перечнем логических операций различают три
основных логических элемента (ЛЭ): И, ИЛИ, НЕ.
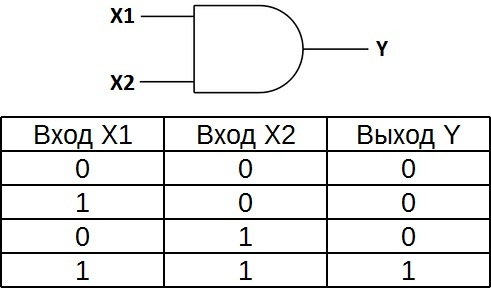
Логический элемент «И» - конъюнкция, логическое умножение, AND
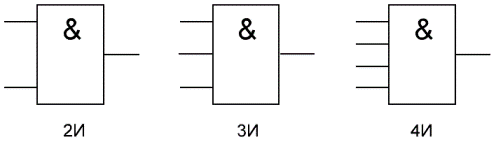
«И» - логический элемент, выполняющий над входными данными операцию конъюнкции или логического умножения. Данный элемент может иметь от 2 до 8 (наиболее распространены в производстве элементы «И» с 2, 3, 4 и 8 входами) входов и один выход.
Логический элемент «ИЛИ» - дизъюнкция, логическое сложение, OR
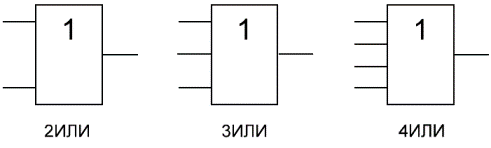
«ИЛИ» - логический элемент, выполняющий над входными данными операцию дизъюнкции или логического сложения. Он так же как и элемент «И» выпускается с двумя, тремя, четырьмя и т. д. входами и с одним выходом. Условные обозначения логических элементов «ИЛИ» с различным количеством входов показаны на рисунке. Обозначаются данные элементы так: 2ИЛИ, 3ИЛИ, 4ИЛИ и т. д.
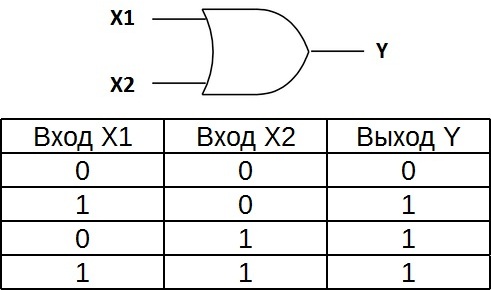
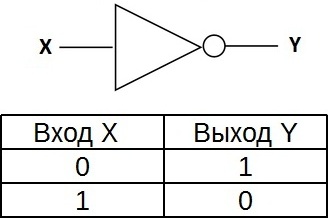
Логический элемент «НЕ» - отрицание, инвертор, NOT
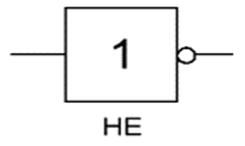
«НЕ» - логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».
Синтез комбинированных цепей. Диаграмма Вейча
Этапы синтеза: 1. Составляется таблица функционирования логической цепи - таблица истинности. Эта таблица показывает, чему равен выходной сигнал цепи при различных сочетаниях входных сигналов; 2. Исходя из таблицы истинности записывается логическая функция; 3. Логическая функция минимизируется и преобразуется к виду, удобному для реализации на логических ячейках заданного типа
Пусть необходимо построить мажоритарную ячейку на три входа, т. е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно единиц.
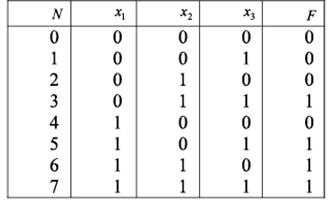
Таблица истинности
Логическая функция
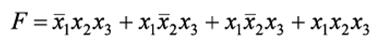
Минимизация:
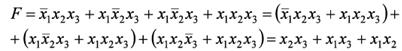
Для элементов И-НЕ:
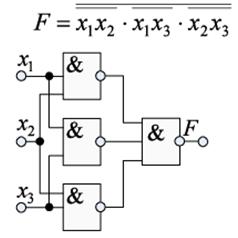
Диаграмма Вейча прямоугольная таблица, в которой число клеток равно числу возможных минтермов. Каждой клетке таблицы ставится в соответствие определенная конъюнкция, причем делается это таким образом, чтобы в соседних клетках (снизу и сверху, слева и справа) конъюнкции отличались не более чем одним сомножителем. При заполнении таблицы в соответствующую клетку ставится 1, если минимизируемая функция при данном наборе аргументов равна единице. В остальные клетки таблицы вписываются нули.
Правила проведения контуров: контур должен быть прямоугольным; внутри контура должны быть только клетки, заполненные единицами; число клеток, находящихся внутри контура, должно быть целой степенью числа 2, т.е. может быть равно 1, 2, 4, 8...; одни и те же клетки, заполненные единицами, могут входить в несколько контуров; при проведении контуров самая нижняя и самая верхняя строки таблицы считаются соседними, то же - для крайнего левого и крайнего правого столбцов; число контуров должно быть как можно меньшим, а сами контуры как можно большими.
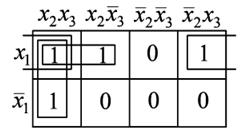
При проведение контуров, охватывающий единицы первый и четвертый столбцы считаются соседними, диаграмму можно представить себе как бы свернутой в виде цилиндра. Для того чтобы найти логическое выражение, которое описывает в диаграмме Вейча контур, охватывающий единицы, нужно рассмотреть обозначения строк и столбцов, входящих в этот контур, и исключить из этих обозначений те аргументы, которые изменяют свое значение внутри контура. Если, например, контур охватывает столбцы х2х3и х2х3, то аргумент х3 из обозначения контура следует исключить. Учитывая, что этот контур располагается в строке x1 получаем окончательное обозначение контура x1x2 Выписывая, таким образом, обозначения всех трех контуров, находим выражение, уже полученное нами ранее алгебраическим путем:
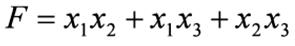
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!